Greedy Criterion in Orthogonal Greedy Learning
Paper and Code
Apr 20, 2016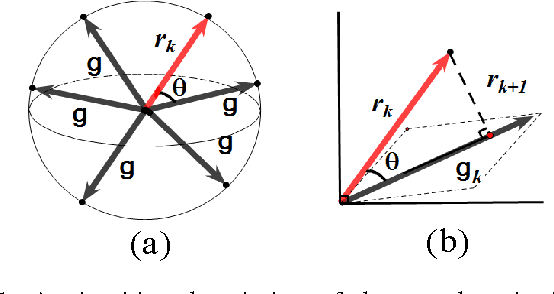
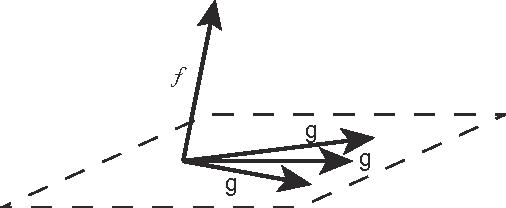
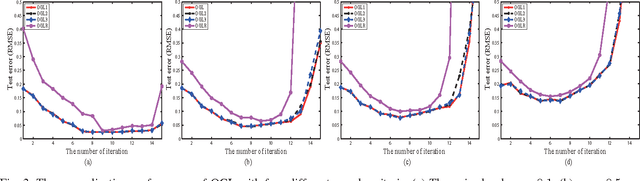
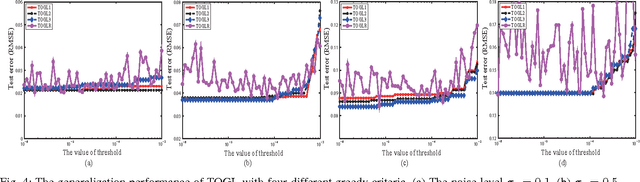
Orthogonal greedy learning (OGL) is a stepwise learning scheme that starts with selecting a new atom from a specified dictionary via the steepest gradient descent (SGD) and then builds the estimator through orthogonal projection. In this paper, we find that SGD is not the unique greedy criterion and introduce a new greedy criterion, called "$\delta$-greedy threshold" for learning. Based on the new greedy criterion, we derive an adaptive termination rule for OGL. Our theoretical study shows that the new learning scheme can achieve the existing (almost) optimal learning rate of OGL. Plenty of numerical experiments are provided to support that the new scheme can achieve almost optimal generalization performance, while requiring less computation than OGL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge