RepoMasterEval: Evaluating Code Completion via Real-World Repositories

With the growing reliance on automated code completion tools in software development, the need for robust evaluation benchmarks has become critical. However, existing benchmarks focus more on code generation tasks in function and class level and provide rich text description to prompt the model. By contrast, such descriptive prompt is commonly unavailable in real development and code completion can occur in wider range of situations such as in the middle of a function or a code block. These limitations makes the evaluation poorly align with the practical scenarios of code completion tools. In this paper, we propose RepoMasterEval, a novel benchmark for evaluating code completion models constructed from real-world Python and TypeScript repositories. Each benchmark datum is generated by masking a code snippet (ground truth) from one source code file with existing test suites. To improve test accuracy of model generated code, we employ mutation testing to measure the effectiveness of the test cases and we manually crafted new test cases for those test suites with low mutation score. Our empirical evaluation on 6 state-of-the-art models shows that test argumentation is critical in improving the accuracy of the benchmark and RepoMasterEval is able to report difference in model performance in real-world scenarios. The deployment of RepoMasterEval in a collaborated company for one month also revealed that the benchmark is useful to give accurate feedback during model training and the score is in high correlation with the model's performance in practice. Based on our findings, we call for the software engineering community to build more LLM benchmarks tailored for code generation tools taking the practical and complex development environment into consideration.

Mitigating barren plateaus of variational quantum eigensolvers

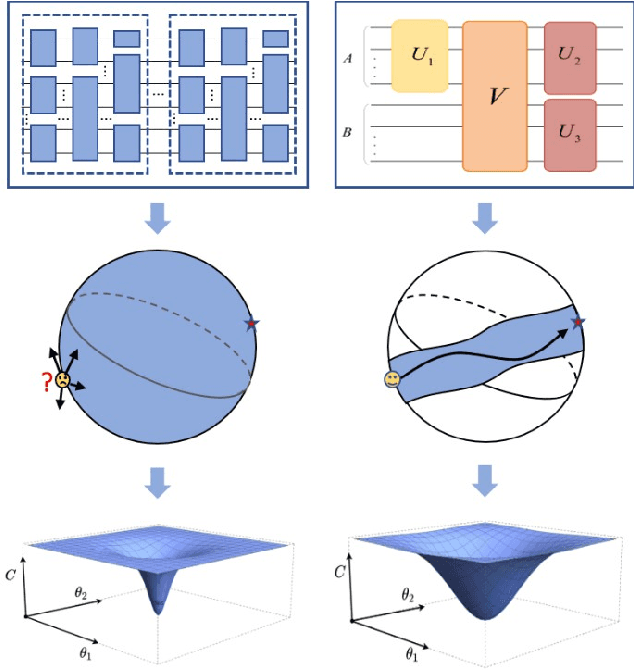
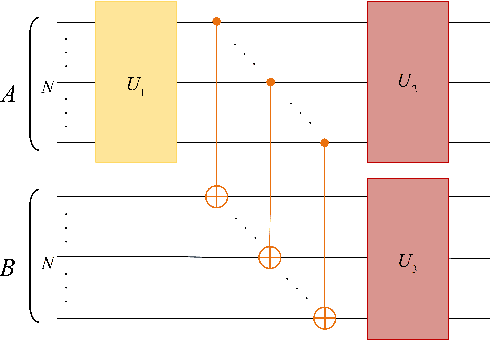
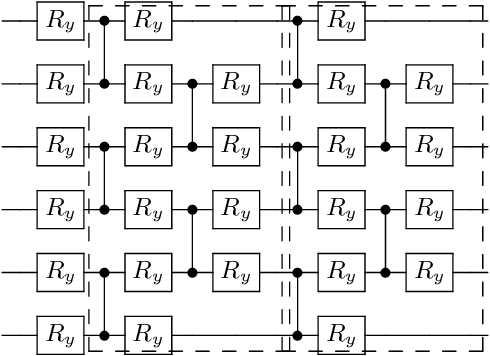
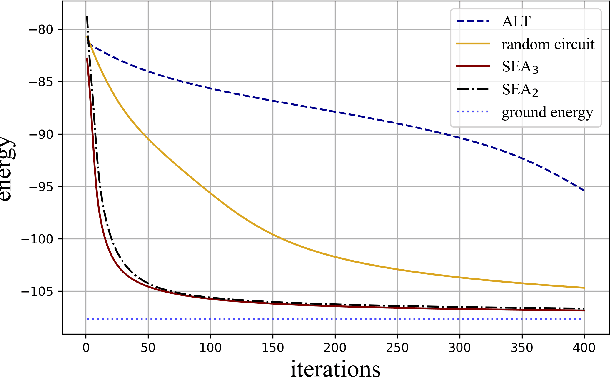
Variational quantum algorithms (VQAs) are expected to establish valuable applications on near-term quantum computers. However, recent works have pointed out that the performance of VQAs greatly relies on the capability of the ansatzes and is seriously limited by optimization issues such as barren plateaus (i.e., vanishing gradients). This work proposes the state efficient ansatz (SEA) for accurate quantum dynamics simulations with improved trainability. First, we show that SEA can generate an arbitrary pure state with much fewer parameters than a universal ansatz, making it efficient for tasks like ground state estimation. It also has the flexibility in adjusting the entanglement of the prepared state, which could be applied to further improve the efficiency of simulating weak entanglement. Second, we show that SEA is not a unitary 2-design even if it has universal wavefunction expressibility and thus has great potential to improve the trainability by avoiding the zone of barren plateaus. We further investigate a plethora of examples in ground state estimation and notably obtain significant improvements in the variances of derivatives and the overall optimization behaviors. This result indicates that SEA can mitigate barren plateaus by sacrificing the redundant expressibility for the target problem.

Approximation smooth and sparse functions by deep neural networks without saturation

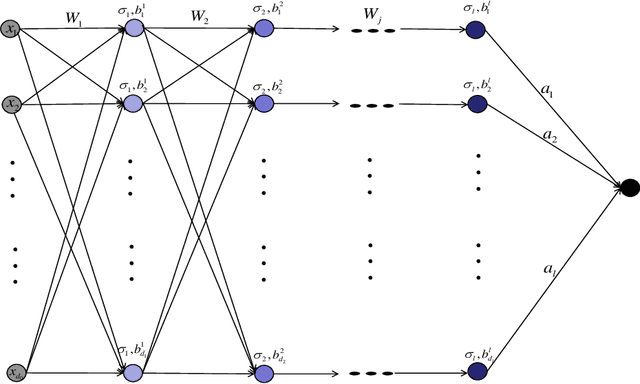
Constructing neural networks for function approximation is a classical and longstanding topic in approximation theory. In this paper, we aim at constructing deep neural networks (deep nets for short) with three hidden layers to approximate smooth and sparse functions. In particular, we prove that the constructed deep nets can reach the optimal approximation rate in approximating both smooth and sparse functions with controllable magnitude of free parameters. Since the saturation that describes the bottleneck of approximate is an insurmountable problem of constructive neural networks, we also prove that deepening the neural network with only one more hidden layer can avoid the saturation. The obtained results underlie advantages of deep nets and provide theoretical explanations for deep learning.

Greedy Criterion in Orthogonal Greedy Learning

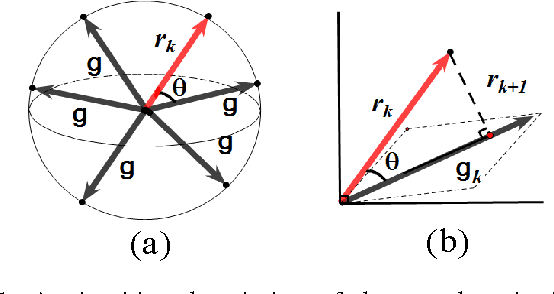
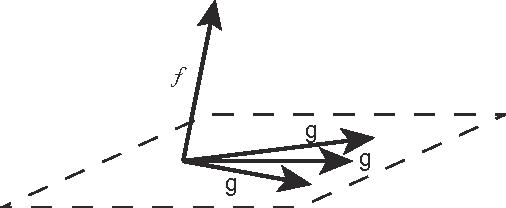
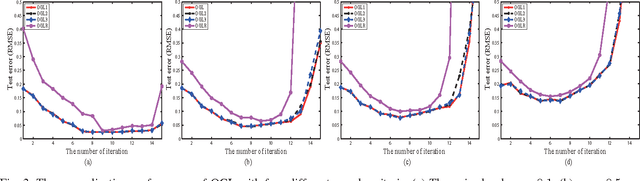
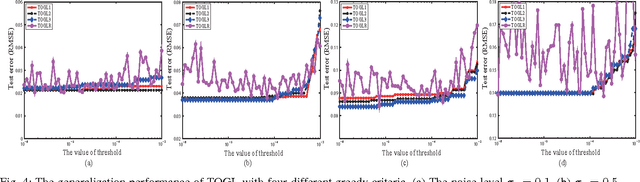
Orthogonal greedy learning (OGL) is a stepwise learning scheme that starts with selecting a new atom from a specified dictionary via the steepest gradient descent (SGD) and then builds the estimator through orthogonal projection. In this paper, we find that SGD is not the unique greedy criterion and introduce a new greedy criterion, called "$\delta$-greedy threshold" for learning. Based on the new greedy criterion, we derive an adaptive termination rule for OGL. Our theoretical study shows that the new learning scheme can achieve the existing (almost) optimal learning rate of OGL. Plenty of numerical experiments are provided to support that the new scheme can achieve almost optimal generalization performance, while requiring less computation than OGL.

Is Extreme Learning Machine Feasible? A Theoretical Assessment (Part II)

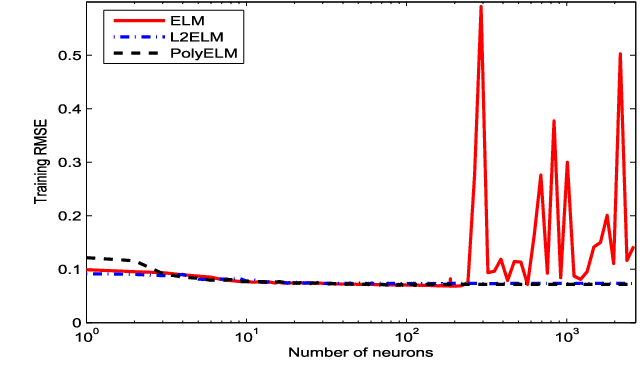
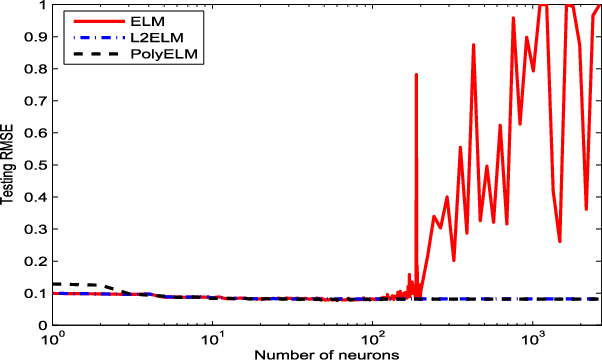
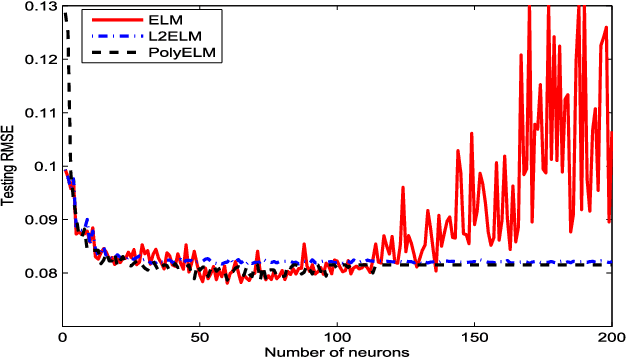
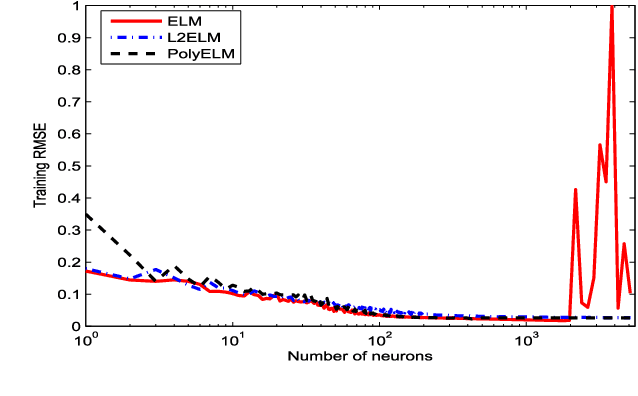
An extreme learning machine (ELM) can be regarded as a two stage feed-forward neural network (FNN) learning system which randomly assigns the connections with and within hidden neurons in the first stage and tunes the connections with output neurons in the second stage. Therefore, ELM training is essentially a linear learning problem, which significantly reduces the computational burden. Numerous applications show that such a computation burden reduction does not degrade the generalization capability. It has, however, been open that whether this is true in theory. The aim of our work is to study the theoretical feasibility of ELM by analyzing the pros and cons of ELM. In the previous part on this topic, we pointed out that via appropriate selection of the activation function, ELM does not degrade the generalization capability in the expectation sense. In this paper, we launch the study in a different direction and show that the randomness of ELM also leads to certain negative consequences. On one hand, we find that the randomness causes an additional uncertainty problem of ELM, both in approximation and learning. On the other hand, we theoretically justify that there also exists an activation function such that the corresponding ELM degrades the generalization capability. In particular, we prove that the generalization capability of ELM with Gaussian kernel is essentially worse than that of FNN with Gaussian kernel. To facilitate the use of ELM, we also provide a remedy to such a degradation. We find that the well-developed coefficient regularization technique can essentially improve the generalization capability. The obtained results reveal the essential characteristic of ELM and give theoretical guidance concerning how to use ELM.