Approximation smooth and sparse functions by deep neural networks without saturation
Paper and Code
Jan 13, 2020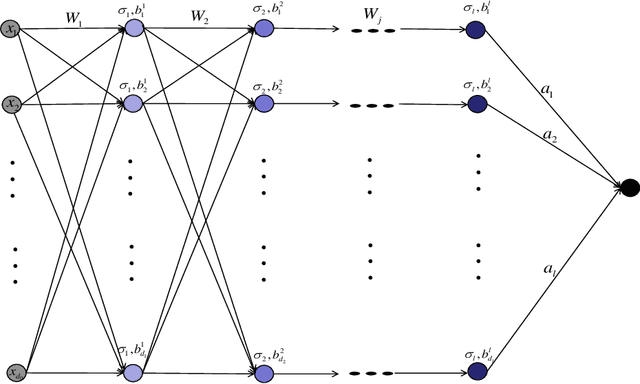
Constructing neural networks for function approximation is a classical and longstanding topic in approximation theory. In this paper, we aim at constructing deep neural networks (deep nets for short) with three hidden layers to approximate smooth and sparse functions. In particular, we prove that the constructed deep nets can reach the optimal approximation rate in approximating both smooth and sparse functions with controllable magnitude of free parameters. Since the saturation that describes the bottleneck of approximate is an insurmountable problem of constructive neural networks, we also prove that deepening the neural network with only one more hidden layer can avoid the saturation. The obtained results underlie advantages of deep nets and provide theoretical explanations for deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge