Is Extreme Learning Machine Feasible? A Theoretical Assessment (Part II)
Paper and Code
Jan 24, 2014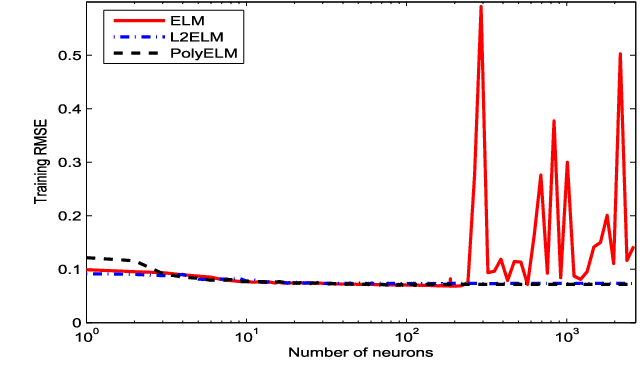
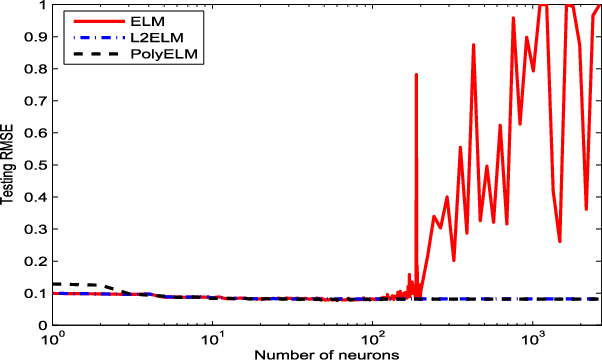
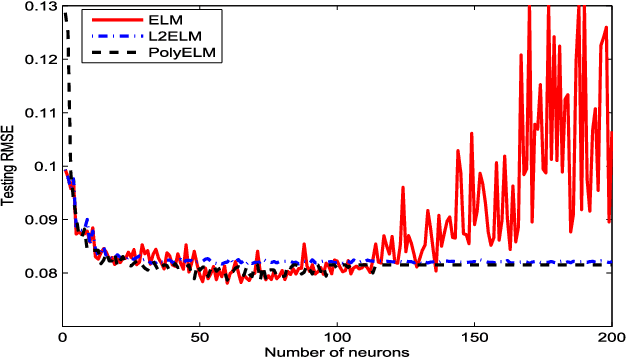
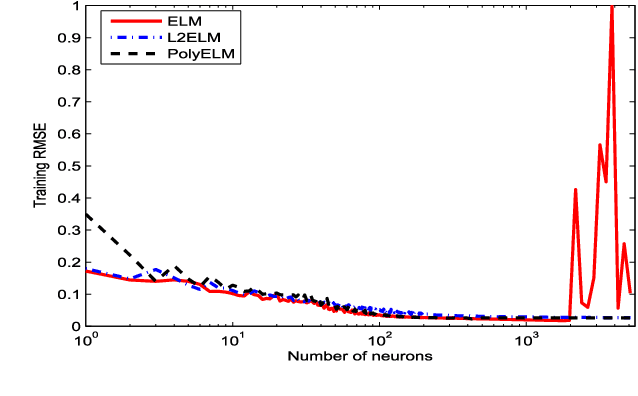
An extreme learning machine (ELM) can be regarded as a two stage feed-forward neural network (FNN) learning system which randomly assigns the connections with and within hidden neurons in the first stage and tunes the connections with output neurons in the second stage. Therefore, ELM training is essentially a linear learning problem, which significantly reduces the computational burden. Numerous applications show that such a computation burden reduction does not degrade the generalization capability. It has, however, been open that whether this is true in theory. The aim of our work is to study the theoretical feasibility of ELM by analyzing the pros and cons of ELM. In the previous part on this topic, we pointed out that via appropriate selection of the activation function, ELM does not degrade the generalization capability in the expectation sense. In this paper, we launch the study in a different direction and show that the randomness of ELM also leads to certain negative consequences. On one hand, we find that the randomness causes an additional uncertainty problem of ELM, both in approximation and learning. On the other hand, we theoretically justify that there also exists an activation function such that the corresponding ELM degrades the generalization capability. In particular, we prove that the generalization capability of ELM with Gaussian kernel is essentially worse than that of FNN with Gaussian kernel. To facilitate the use of ELM, we also provide a remedy to such a degradation. We find that the well-developed coefficient regularization technique can essentially improve the generalization capability. The obtained results reveal the essential characteristic of ELM and give theoretical guidance concerning how to use ELM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge