Jian Fang
Perspective-Invariant 3D Object Detection
Jul 23, 2025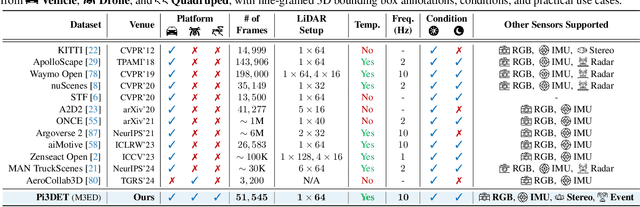
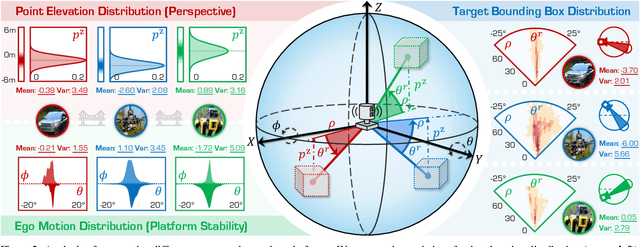
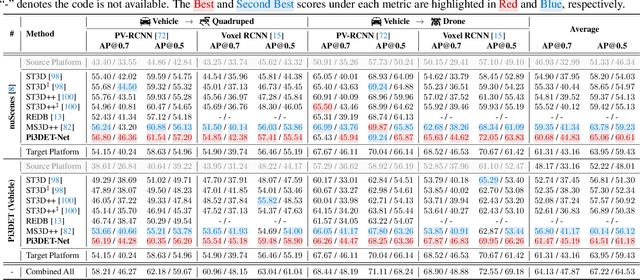
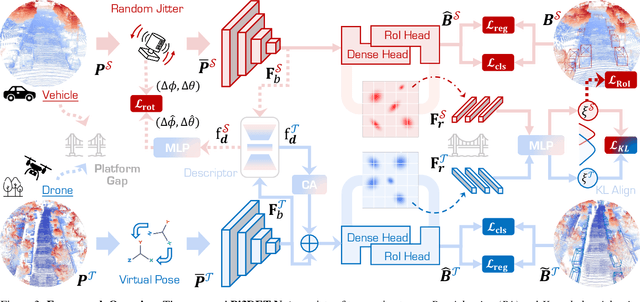
Abstract:With the rise of robotics, LiDAR-based 3D object detection has garnered significant attention in both academia and industry. However, existing datasets and methods predominantly focus on vehicle-mounted platforms, leaving other autonomous platforms underexplored. To bridge this gap, we introduce Pi3DET, the first benchmark featuring LiDAR data and 3D bounding box annotations collected from multiple platforms: vehicle, quadruped, and drone, thereby facilitating research in 3D object detection for non-vehicle platforms as well as cross-platform 3D detection. Based on Pi3DET, we propose a novel cross-platform adaptation framework that transfers knowledge from the well-studied vehicle platform to other platforms. This framework achieves perspective-invariant 3D detection through robust alignment at both geometric and feature levels. Additionally, we establish a benchmark to evaluate the resilience and robustness of current 3D detectors in cross-platform scenarios, providing valuable insights for developing adaptive 3D perception systems. Extensive experiments validate the effectiveness of our approach on challenging cross-platform tasks, demonstrating substantial gains over existing adaptation methods. We hope this work paves the way for generalizable and unified 3D perception systems across diverse and complex environments. Our Pi3DET dataset, cross-platform benchmark suite, and annotation toolkit have been made publicly available.
PDM-SSD: Single-Stage Three-Dimensional Object Detector With Point Dilation
Feb 10, 2025



Abstract:Current Point-based detectors can only learn from the provided points, with limited receptive fields and insufficient global learning capabilities for such targets. In this paper, we present a novel Point Dilation Mechanism for single-stage 3D detection (PDM-SSD) that takes advantage of these two representations. Specifically, we first use a PointNet-style 3D backbone for efficient feature encoding. Then, a neck with Point Dilation Mechanism (PDM) is used to expand the feature space, which involves two key steps: point dilation and feature filling. The former expands points to a certain size grid centered around the sampled points in Euclidean space. The latter fills the unoccupied grid with feature for backpropagation using spherical harmonic coefficients and Gaussian density function in terms of direction and scale. Next, we associate multiple dilation centers and fuse coefficients to obtain sparse grid features through height compression. Finally, we design a hybrid detection head for joint learning, where on one hand, the scene heatmap is predicted to complement the voting point set for improved detection accuracy, and on the other hand, the target probability of detected boxes are calibrated through feature fusion. On the challenging Karlsruhe Institute of Technology and Toyota Technological Institute (KITTI) dataset, PDM-SSD achieves state-of-the-art results for multi-class detection among single-modal methods with an inference speed of 68 frames. We also demonstrate the advantages of PDM-SSD in detecting sparse and incomplete objects through numerous object-level instances. Additionally, PDM can serve as an auxiliary network to establish a connection between sampling points and object centers, thereby improving the accuracy of the model without sacrificing inference speed. Our code will be available at https://github.com/AlanLiangC/PDM-SSD.git.
SGCCNet: Single-Stage 3D Object Detector With Saliency-Guided Data Augmentation and Confidence Correction Mechanism
Jul 01, 2024



Abstract:The single-stage point-based 3D object detectors have attracted widespread research interest due to their advantages of lightweight and fast inference speed. However, they still face challenges such as inadequate learning of low-quality objects (ILQ) and misalignment between localization accuracy and classification confidence (MLC). In this paper, we propose SGCCNet to alleviate these two issues. For ILQ, SGCCNet adopts a Saliency-Guided Data Augmentation (SGDA) strategy to enhance the robustness of the model on low-quality objects by reducing its reliance on salient features. Specifically, We construct a classification task and then approximate the saliency scores of points by moving points towards the point cloud centroid in a differentiable process. During the training process, SGCCNet will be forced to learn from low saliency features through dropping points. Meanwhile, to avoid internal covariate shift and contextual features forgetting caused by dropping points, we add a geometric normalization module and skip connection block in each stage. For MLC, we design a Confidence Correction Mechanism (CCM) specifically for point-based multi-class detectors. This mechanism corrects the confidence of the current proposal by utilizing the predictions of other key points within the local region in the post-processing stage. Extensive experiments on the KITTI dataset demonstrate the generality and effectiveness of our SGCCNet. On the KITTI \textit{test} set, SGCCNet achieves $80.82\%$ for the metric of $AP_{3D}$ on the \textit{Moderate} level, outperforming all other point-based detectors, surpassing IA-SSD and Fast Point R-CNN by $2.35\%$ and $3.42\%$, respectively. Additionally, SGCCNet demonstrates excellent portability for other point-based detectors
Hyperspectral and LiDAR data classification based on linear self-attention
Apr 06, 2021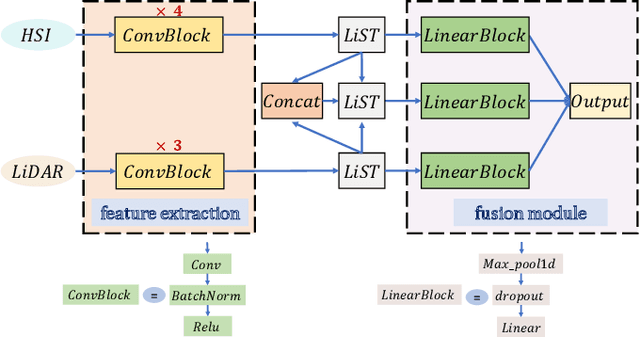
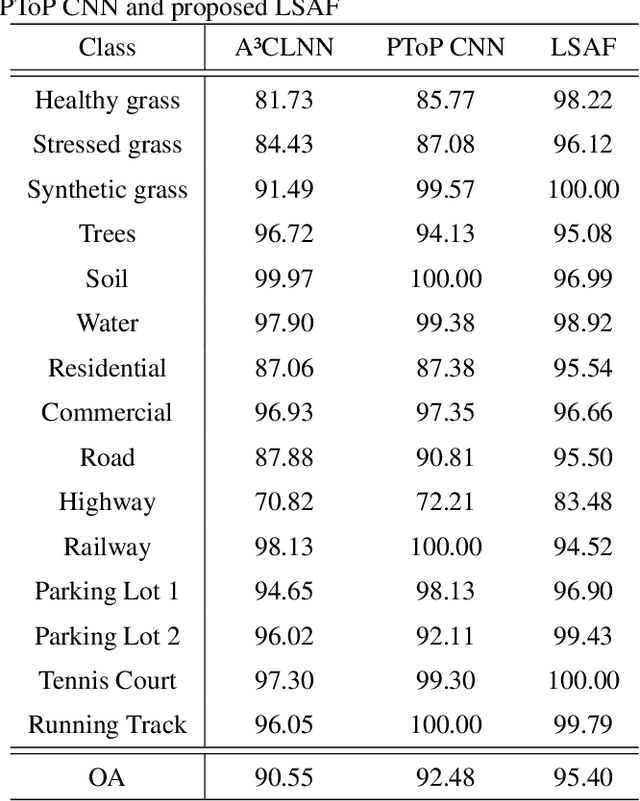
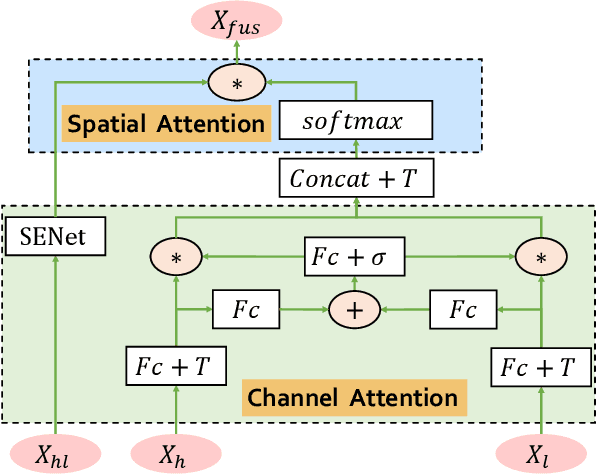
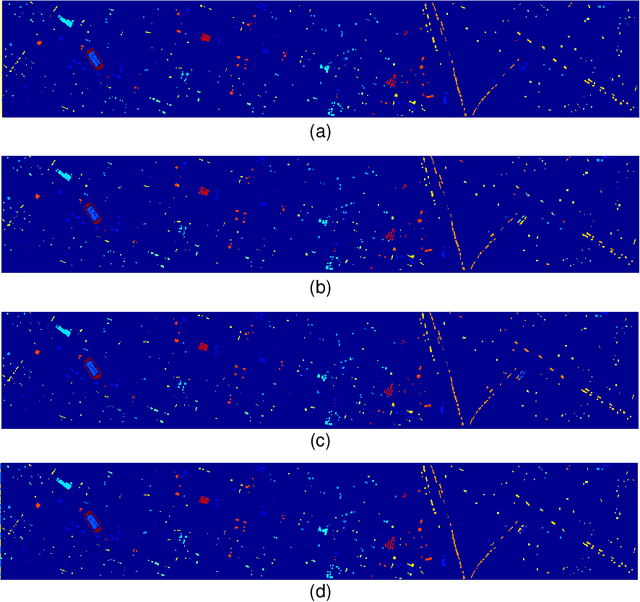
Abstract:An efficient linear self-attention fusion model is proposed in this paper for the task of hyperspectral image (HSI) and LiDAR data joint classification. The proposed method is comprised of a feature extraction module, an attention module, and a fusion module. The attention module is a plug-and-play linear self-attention module that can be extensively used in any model. The proposed model has achieved the overall accuracy of 95.40\% on the Houston dataset. The experimental results demonstrate the superiority of the proposed method over other state-of-the-art models.
Hierarchical Text Interaction for Rating Prediction
Oct 15, 2020



Abstract:Traditional recommender systems encounter several challenges such as data sparsity and unexplained recommendation. To address these challenges, many works propose to exploit semantic information from review data. However, these methods have two major limitations in terms of the way to model textual features and capture textual interaction. For textual modeling, they simply concatenate all the reviews of a user/item into a single review. However, feature extraction at word/phrase level can violate the meaning of the original reviews. As for textual interaction, they defer the interactions to the prediction layer, making them fail to capture complex correlations between users and items. To address those limitations, we propose a novel Hierarchical Text Interaction model(HTI) for rating prediction. In HTI, we propose to model low-level word semantics and high-level review representations hierarchically. The hierarchy allows us to exploit textual features at different granularities. To further capture complex user-item interactions, we propose to exploit semantic correlations between each user-item pair at different hierarchies. At word level, we propose an attention mechanism specialized to each user-item pair, and capture the important words for representing each review. At review level, we mutually propagate textual features between the user and item, and capture the informative reviews. The aggregated review representations are integrated into a collaborative filtering framework for rating prediction. Experiments on five real-world datasets demonstrate that HTI outperforms state-of-the-art models by a large margin. Further case studies provide a deep insight into HTI's ability to capture semantic correlations at different levels of granularities for rating prediction.
Learning through deterministic assignment of hidden parameters
Sep 13, 2018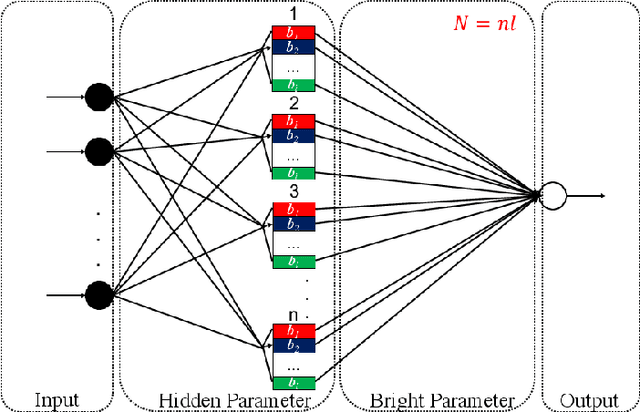
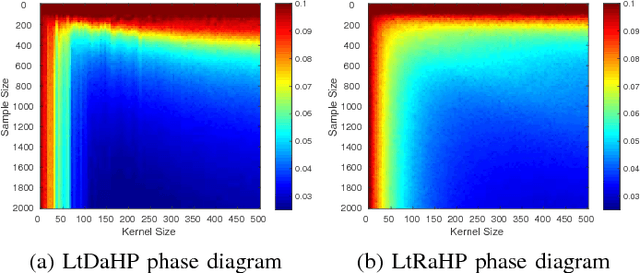
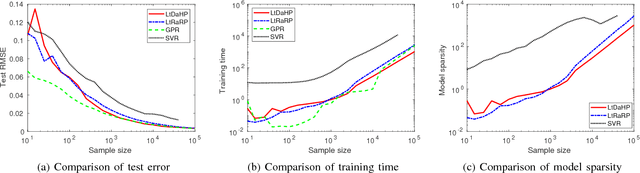
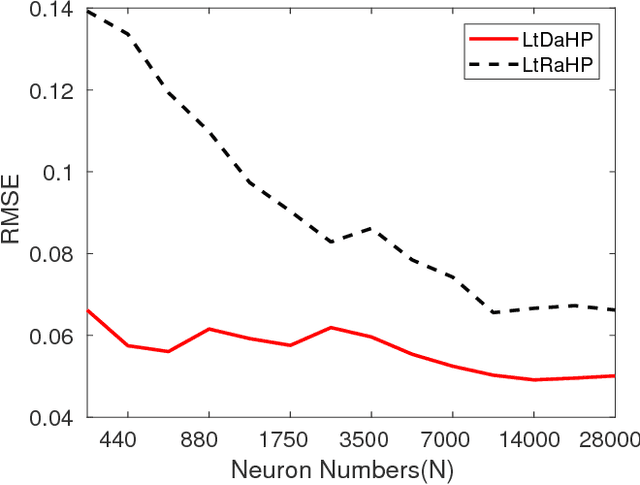
Abstract:Supervised learning frequently boils down to determining hidden and bright parameters in a parameterized hypothesis space based on finite input-output samples. The hidden parameters determine the attributions of hidden predictors or the nonlinear mechanism of an estimator, while the bright parameters characterize how hidden predictors are linearly combined or the linear mechanism. In traditional learning paradigm, hidden and bright parameters are not distinguished and trained simultaneously in one learning process. Such an one-stage learning (OSL) brings a benefit of theoretical analysis but suffers from the high computational burden. To overcome this difficulty, a two-stage learning (TSL) scheme, featured by learning through deterministic assignment of hidden parameters (LtDaHP) was proposed, which suggests to deterministically generate the hidden parameters by using minimal Riesz energy points on a sphere and equally spaced points in an interval. We theoretically show that with such deterministic assignment of hidden parameters, LtDaHP with a neural network realization almost shares the same generalization performance with that of OSL. We also present a series of simulations and application examples to support the outperformance of LtDaHP
Learning rates of $l^q$ coefficient regularization learning with Gaussian kernel
Sep 25, 2014Abstract:Regularization is a well recognized powerful strategy to improve the performance of a learning machine and $l^q$ regularization schemes with $0<q<\infty$ are central in use. It is known that different $q$ leads to different properties of the deduced estimators, say, $l^2$ regularization leads to smooth estimators while $l^1$ regularization leads to sparse estimators. Then, how does the generalization capabilities of $l^q$ regularization learning vary with $q$? In this paper, we study this problem in the framework of statistical learning theory and show that implementing $l^q$ coefficient regularization schemes in the sample dependent hypothesis space associated with Gaussian kernel can attain the same almost optimal learning rates for all $0<q<\infty$. That is, the upper and lower bounds of learning rates for $l^q$ regularization learning are asymptotically identical for all $0<q<\infty$. Our finding tentatively reveals that, in some modeling contexts, the choice of $q$ might not have a strong impact with respect to the generalization capability. From this perspective, $q$ can be arbitrarily specified, or specified merely by other no generalization criteria like smoothness, computational complexity, sparsity, etc..
Learning and approximation capability of orthogonal super greedy algorithm
Sep 18, 2014



Abstract:We consider the approximation capability of orthogonal super greedy algorithms (OSGA) and its applications in supervised learning. OSGA is concerned with selecting more than one atoms in each iteration step, which, of course, greatly reduces the computational burden when compared with the conventional orthogonal greedy algorithm (OGA). We prove that even for function classes that are not the convex hull of the dictionary, OSGA does not degrade the approximation capability of OGA provided the dictionary is incoherent. Based on this, we deduce a tight generalization error bound for OSGA learning. Our results show that in the realm of supervised learning, OSGA provides a possibility to further reduce the computational burden of OGA in the premise of maintaining its prominent generalization capability.
Is Extreme Learning Machine Feasible? A Theoretical Assessment (Part II)
Jan 24, 2014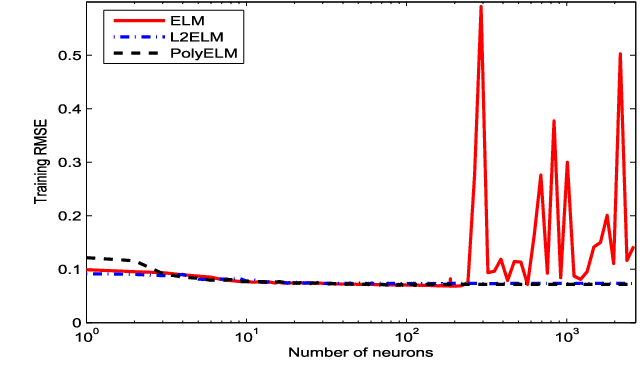
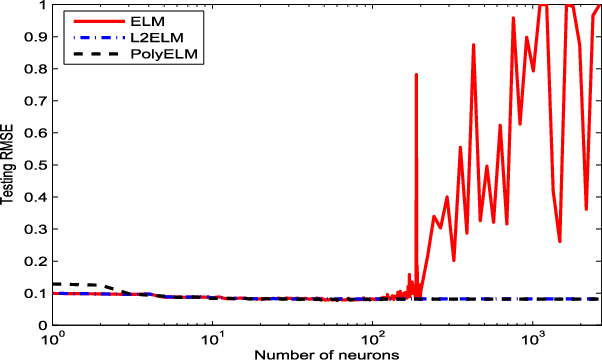
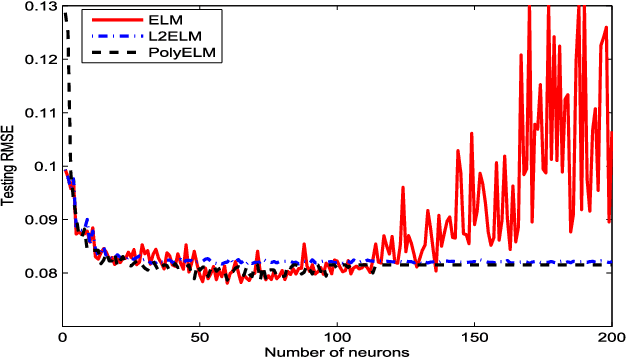
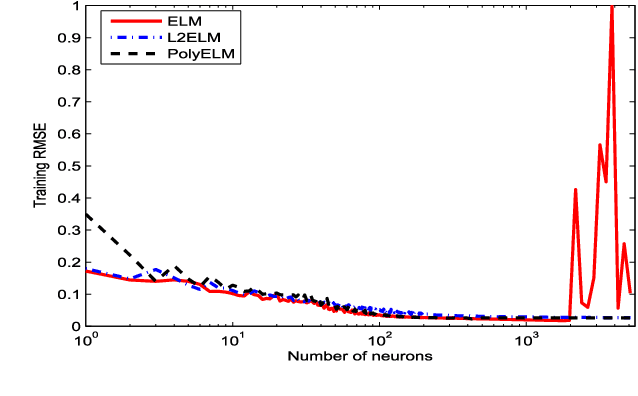
Abstract:An extreme learning machine (ELM) can be regarded as a two stage feed-forward neural network (FNN) learning system which randomly assigns the connections with and within hidden neurons in the first stage and tunes the connections with output neurons in the second stage. Therefore, ELM training is essentially a linear learning problem, which significantly reduces the computational burden. Numerous applications show that such a computation burden reduction does not degrade the generalization capability. It has, however, been open that whether this is true in theory. The aim of our work is to study the theoretical feasibility of ELM by analyzing the pros and cons of ELM. In the previous part on this topic, we pointed out that via appropriate selection of the activation function, ELM does not degrade the generalization capability in the expectation sense. In this paper, we launch the study in a different direction and show that the randomness of ELM also leads to certain negative consequences. On one hand, we find that the randomness causes an additional uncertainty problem of ELM, both in approximation and learning. On the other hand, we theoretically justify that there also exists an activation function such that the corresponding ELM degrades the generalization capability. In particular, we prove that the generalization capability of ELM with Gaussian kernel is essentially worse than that of FNN with Gaussian kernel. To facilitate the use of ELM, we also provide a remedy to such a degradation. We find that the well-developed coefficient regularization technique can essentially improve the generalization capability. The obtained results reveal the essential characteristic of ELM and give theoretical guidance concerning how to use ELM.
Compressed Sensing SAR Imaging with Multilook Processing
Oct 27, 2013
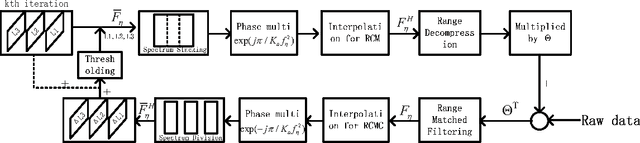


Abstract:Multilook processing is a widely used speckle reduction approach in synthetic aperture radar (SAR) imaging. Conventionally, it is achieved by incoherently summing of some independent low-resolution images formulated from overlapping subbands of the SAR signal. However, in the context of compressive sensing (CS) SAR imaging, where the samples are collected at sub-Nyquist rate, the data spectrum is highly aliased that hinders the direct application of the existing multilook techniques. In this letter, we propose a new CS-SAR imaging method that can realize multilook processing simultaneously during image reconstruction. The main idea is to replace the SAR observation matrix by the inverse of multilook procedures, which is then combined with random sampling matrix to yield a multilook CS-SAR observation model. Then a joint sparse regularization model, considering pixel dependency of subimages, is derived to form multilook images. The suggested SAR imaging method can not only reconstruct sparse scene efficiently below Nyquist rate, but is also able to achieve a comparable reduction of speckles during reconstruction. Simulation results are finally provided to demonstrate the effectiveness of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge