Learning through deterministic assignment of hidden parameters

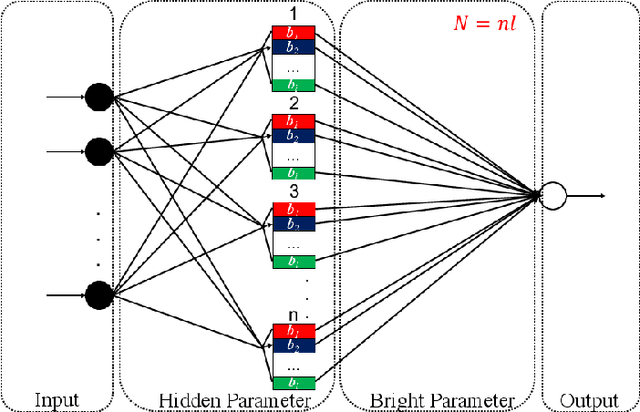
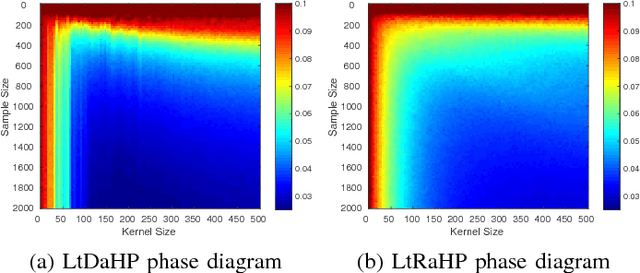
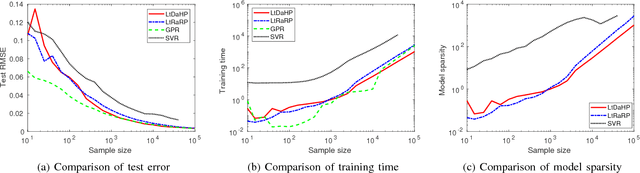
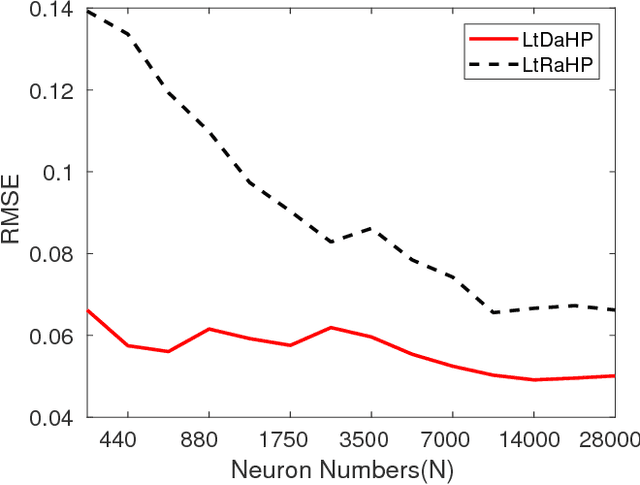
Supervised learning frequently boils down to determining hidden and bright parameters in a parameterized hypothesis space based on finite input-output samples. The hidden parameters determine the attributions of hidden predictors or the nonlinear mechanism of an estimator, while the bright parameters characterize how hidden predictors are linearly combined or the linear mechanism. In traditional learning paradigm, hidden and bright parameters are not distinguished and trained simultaneously in one learning process. Such an one-stage learning (OSL) brings a benefit of theoretical analysis but suffers from the high computational burden. To overcome this difficulty, a two-stage learning (TSL) scheme, featured by learning through deterministic assignment of hidden parameters (LtDaHP) was proposed, which suggests to deterministically generate the hidden parameters by using minimal Riesz energy points on a sphere and equally spaced points in an interval. We theoretically show that with such deterministic assignment of hidden parameters, LtDaHP with a neural network realization almost shares the same generalization performance with that of OSL. We also present a series of simulations and application examples to support the outperformance of LtDaHP