Mitigating barren plateaus of variational quantum eigensolvers
Paper and Code
May 26, 2022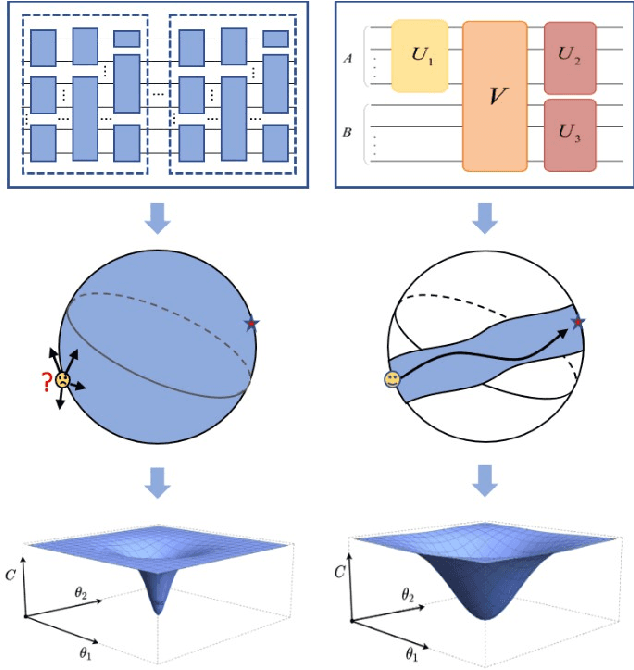
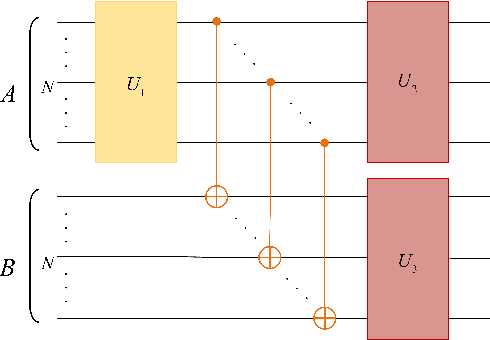
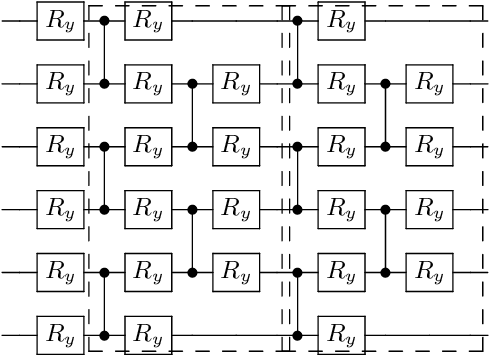
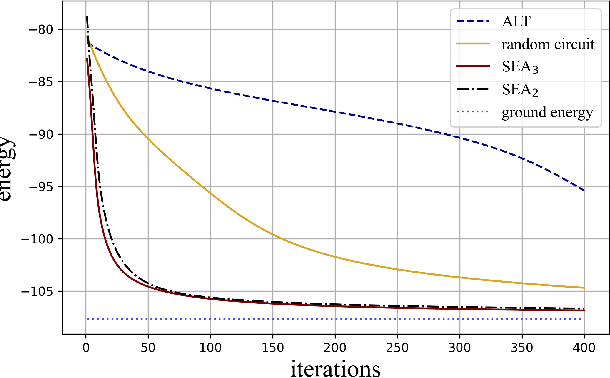
Variational quantum algorithms (VQAs) are expected to establish valuable applications on near-term quantum computers. However, recent works have pointed out that the performance of VQAs greatly relies on the capability of the ansatzes and is seriously limited by optimization issues such as barren plateaus (i.e., vanishing gradients). This work proposes the state efficient ansatz (SEA) for accurate quantum dynamics simulations with improved trainability. First, we show that SEA can generate an arbitrary pure state with much fewer parameters than a universal ansatz, making it efficient for tasks like ground state estimation. It also has the flexibility in adjusting the entanglement of the prepared state, which could be applied to further improve the efficiency of simulating weak entanglement. Second, we show that SEA is not a unitary 2-design even if it has universal wavefunction expressibility and thus has great potential to improve the trainability by avoiding the zone of barren plateaus. We further investigate a plethora of examples in ground state estimation and notably obtain significant improvements in the variances of derivatives and the overall optimization behaviors. This result indicates that SEA can mitigate barren plateaus by sacrificing the redundant expressibility for the target problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge