Wasserstein Distributionally Robust Optimization via Wasserstein Barycenters
Paper and Code
Mar 23, 2022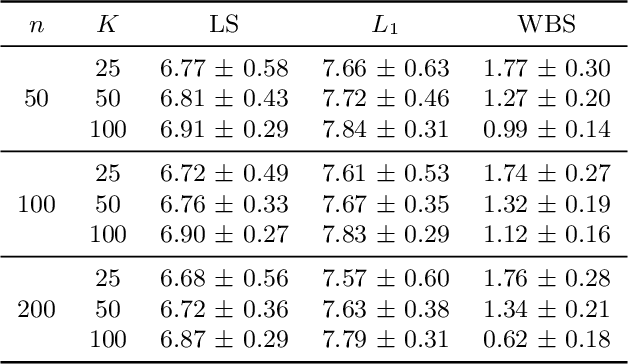
In many applications in statistics and machine learning, the availability of data samples from multiple sources has become increasingly prevalent. On the other hand, in distributionally robust optimization, we seek data-driven decisions which perform well under the most adverse distribution from a nominal distribution constructed from data samples within a certain distance of probability distributions. However, it remains unclear how to achieve such distributional robustness when data samples from multiple sources are available. In this paper, we propose constructing the nominal distribution in Wasserstein distributionally robust optimization problems through the notion of Wasserstein barycenter as an aggregation of data samples from multiple sources. Under specific choices of the loss function, the proposed formulation admits a tractable reformulation as a finite convex program, with powerful finite-sample and asymptotic guarantees. We illustrate our proposed method through concrete examples with nominal distributions of location-scatter families and distributionally robust maximum likelihood estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge