A Proximal Block Coordinate Descent Algorithm for Deep Neural Network Training
Paper and Code
Mar 24, 2018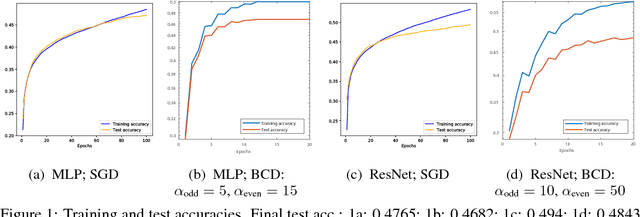
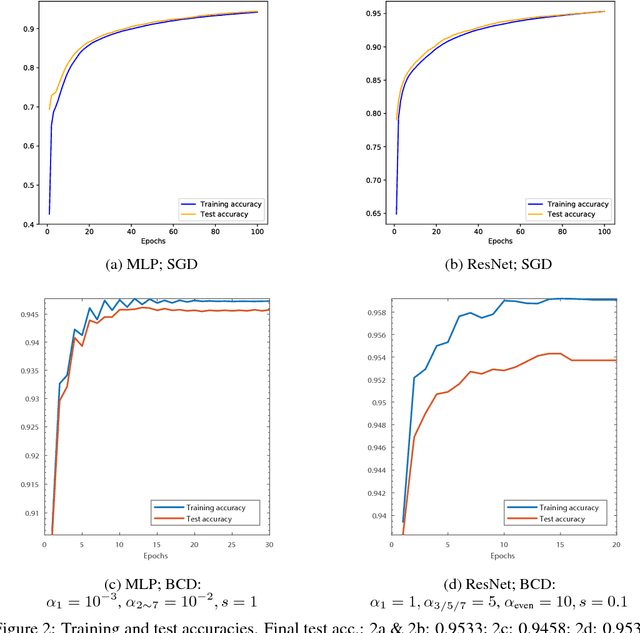
Training deep neural networks (DNNs) efficiently is a challenge due to the associated highly nonconvex optimization. The backpropagation (backprop) algorithm has long been the most widely used algorithm for gradient computation of parameters of DNNs and is used along with gradient descent-type algorithms for this optimization task. Recent work have shown the efficiency of block coordinate descent (BCD) type methods empirically for training DNNs. In view of this, we propose a novel algorithm based on the BCD method for training DNNs and provide its global convergence results built upon the powerful framework of the Kurdyka-Lojasiewicz (KL) property. Numerical experiments on standard datasets demonstrate its competitive efficiency against standard optimizers with backprop.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge