Aligning Compound AI Systems via System-level DPO

Compound AI systems, comprising multiple interacting components such as LLM agents and external tools, demonstrate state-of-the-art results across diverse tasks. It is hence crucial to align components within the system to produce consistent results that match human expectations. However, conventional alignment methods, such as Direct Preference Optimization (DPO), are not directly applicable to compound AI systems. These challenges include the non-differentiable interactions between components, making end-to-end gradient optimization infeasible. Additionally, system-level preferences cannot be directly translated into component-level preferences, further complicating alignment. We address the issues by formulating compound AI systems as Directed Acyclic Graphs (DAGs), capturing the connections between agents and the data generation processes. We propose a system-level DPO (SysDPO) to jointly align compound systems by adapting the DPO to operate on these DAGs. We study the joint alignment of an LLM and a diffusion model to demonstrate the effectiveness of our approach. Our exploration provides insights into the alignment of compound AI systems and lays a foundation for future advancements.

High-Dimensional Markov-switching Ordinary Differential Processes

We investigate the parameter recovery of Markov-switching ordinary differential processes from discrete observations, where the differential equations are nonlinear additive models. This framework has been widely applied in biological systems, control systems, and other domains; however, limited research has been conducted on reconstructing the generating processes from observations. In contrast, many physical systems, such as human brains, cannot be directly experimented upon and rely on observations to infer the underlying systems. To address this gap, this manuscript presents a comprehensive study of the model, encompassing algorithm design, optimization guarantees, and quantification of statistical errors. Specifically, we develop a two-stage algorithm that first recovers the continuous sample path from discrete samples and then estimates the parameters of the processes. We provide novel theoretical insights into the statistical error and linear convergence guarantee when the processes are $\beta$-mixing. Our analysis is based on the truncation of the latent posterior processes and demonstrates that the truncated processes approximate the true processes under mixing conditions. We apply this model to investigate the differences in resting-state brain networks between the ADHD group and normal controls, revealing differences in the transition rate matrices of the two groups.

Proxy Methods for Domain Adaptation

We study the problem of domain adaptation under distribution shift, where the shift is due to a change in the distribution of an unobserved, latent variable that confounds both the covariates and the labels. In this setting, neither the covariate shift nor the label shift assumptions apply. Our approach to adaptation employs proximal causal learning, a technique for estimating causal effects in settings where proxies of unobserved confounders are available. We demonstrate that proxy variables allow for adaptation to distribution shift without explicitly recovering or modeling latent variables. We consider two settings, (i) Concept Bottleneck: an additional ''concept'' variable is observed that mediates the relationship between the covariates and labels; (ii) Multi-domain: training data from multiple source domains is available, where each source domain exhibits a different distribution over the latent confounder. We develop a two-stage kernel estimation approach to adapt to complex distribution shifts in both settings. In our experiments, we show that our approach outperforms other methods, notably those which explicitly recover the latent confounder.

Goodness-of-Fit of Attributed Probabilistic Graph Generative Models

Probabilistic generative models of graphs are important tools that enable representation and sampling. Many recent works have created probabilistic models of graphs that are capable of representing not only entity interactions but also their attributes. However, given a generative model of random attributed graph(s), the general conditions that establish goodness of fit are not clear a-priori. In this paper, we define goodness of fit in terms of the mean square contingency coefficient for random binary networks. For this statistic, we outline a procedure for assessing the quality of the structure of a learned attributed graph by ensuring that the discrepancy of the mean square contingency coefficient (constant, or random) is minimal with high probability. We apply these criteria to verify the representation capability of a probabilistic generative model for various popular types of graph models.

Adapting to Latent Subgroup Shifts via Concepts and Proxies

We address the problem of unsupervised domain adaptation when the source domain differs from the target domain because of a shift in the distribution of a latent subgroup. When this subgroup confounds all observed data, neither covariate shift nor label shift assumptions apply. We show that the optimal target predictor can be non-parametrically identified with the help of concept and proxy variables available only in the source domain, and unlabeled data from the target. The identification results are constructive, immediately suggesting an algorithm for estimating the optimal predictor in the target. For continuous observations, when this algorithm becomes impractical, we propose a latent variable model specific to the data generation process at hand. We show how the approach degrades as the size of the shift changes, and verify that it outperforms both covariate and label shift adjustment.

Latent Multimodal Functional Graphical Model Estimation

Joint multimodal functional data acquisition, where functional data from multiple modes are measured simultaneously from the same subject, has emerged as an exciting modern approach enabled by recent engineering breakthroughs in the neurological and biological sciences. One prominent motivation to acquire such data is to enable new discoveries of the underlying connectivity by combining multimodal signals. Despite the scientific interest, there remains a gap in principled statistical methods for estimating the graph underlying multimodal functional data. To this end, we propose a new integrative framework that models the data generation process and identifies operators mapping from the observation space to the latent space. We then develop an estimator that simultaneously estimates the transformation operators and the latent graph. This estimator is based on the partial correlation operator, which we rigorously extend from the multivariate to the functional setting. Our procedure is provably efficient, with the estimator converging to a stationary point with quantifiable statistical error. Furthermore, we show recovery of the latent graph under mild conditions. Our work is applied to analyze simultaneously acquired multimodal brain imaging data where the graph indicates functional connectivity of the brain. We present simulation and empirical results that support the benefits of joint estimation.

Joint Gaussian Graphical Model Estimation: A Survey

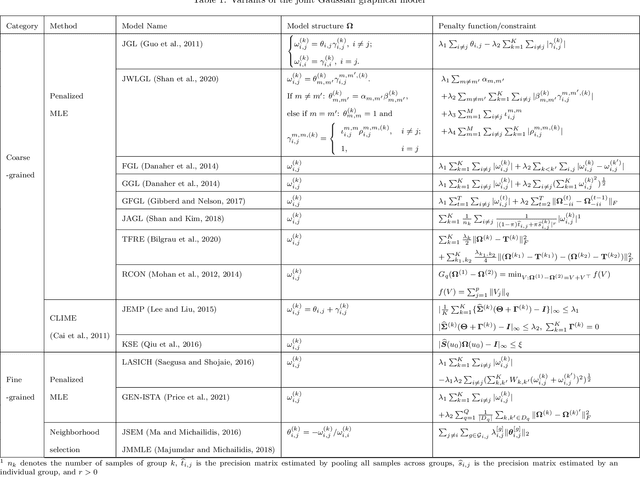
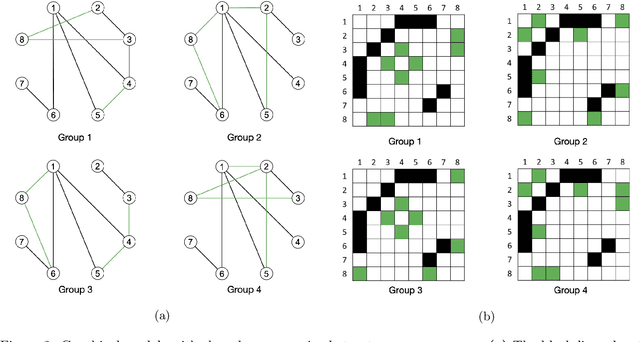
Graphs from complex systems often share a partial underlying structure across domains while retaining individual features. Thus, identifying common structures can shed light on the underlying signal, for instance, when applied to scientific discoveries or clinical diagnoses. Furthermore, growing evidence shows that the shared structure across domains boosts the estimation power of graphs, particularly for high-dimensional data. However, building a joint estimator to extract the common structure may be more complicated than it seems, most often due to data heterogeneity across sources. This manuscript surveys recent work on statistical inference of joint Gaussian graphical models, identifying model structures that fit various data generation processes. Simulations under different data generation processes are implemented with detailed discussions on the choice of models.

A Nonconvex Framework for Structured Dynamic Covariance Recovery

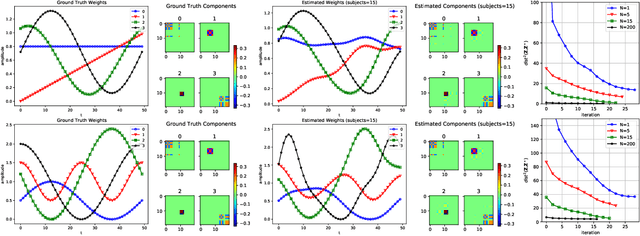
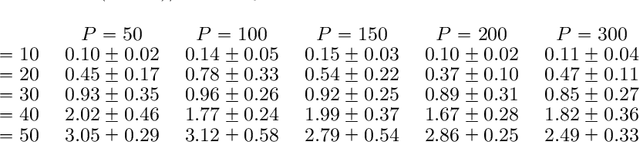
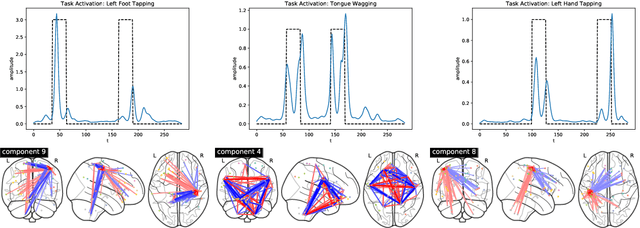
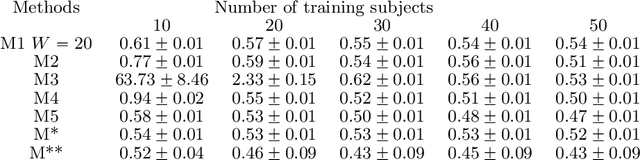
We propose a flexible yet interpretable model for high-dimensional data with time-varying second order statistics, motivated and applied to functional neuroimaging data. Motivated by the neuroscience literature, we factorize the covariances into sparse spatial and smooth temporal components. While this factorization results in both parsimony and domain interpretability, the resulting estimation problem is nonconvex. To this end, we design a two-stage optimization scheme with a carefully tailored spectral initialization, combined with iteratively refined alternating projected gradient descent. We prove a linear convergence rate up to a nontrivial statistical error for the proposed descent scheme and establish sample complexity guarantees for the estimator. We further quantify the statistical error for the multivariate Gaussian case. Empirical results using simulated and real brain imaging data illustrate that our approach outperforms existing baselines.