Estimating shared subspace with AJIVE: the power and limitation of multiple data matrices

Integrative data analysis often requires disentangling joint and individual variations across multiple datasets, a challenge commonly addressed by the Joint and Individual Variation Explained (JIVE) model. While numerous methods have been developed to estimate the shared subspace under JIVE, the theoretical understanding of their performance remains limited, particularly in the context of multiple matrices and varying levels of subspace misalignment. This paper bridges this gap by providing a systematic analysis of shared subspace estimation in multi-matrix settings. We focus on the Angle-based Joint and Individual Variation Explained (AJIVE) method, a two-stage spectral approach, and establish new performance guarantees that uncover its strengths and limitations. Specifically, we show that in high signal-to-noise ratio (SNR) regimes, AJIVE's estimation error decreases with the number of matrices, demonstrating the power of multi-matrix integration. Conversely, in low-SNR settings, AJIVE exhibits a non-diminishing error, highlighting fundamental limitations. To complement these results, we derive minimax lower bounds, showing that AJIVE achieves optimal rates in high-SNR regimes. Furthermore, we analyze an oracle-aided spectral estimator to demonstrate that the non-diminishing error in low-SNR scenarios is a fundamental barrier. Extensive numerical experiments corroborate our theoretical findings, providing insights into the interplay between SNR, matrix count, and subspace misalignment.

Random pairing MLE for estimation of item parameters in Rasch model

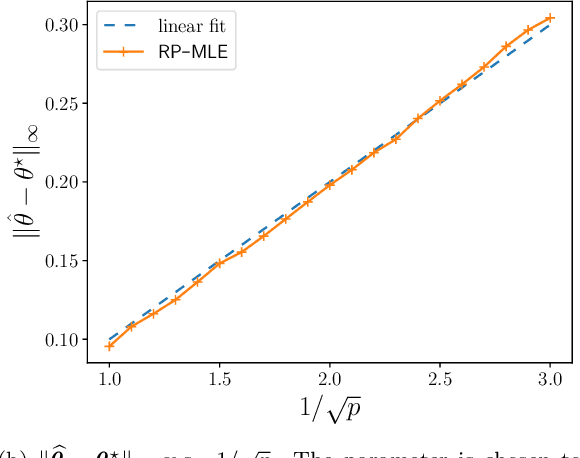
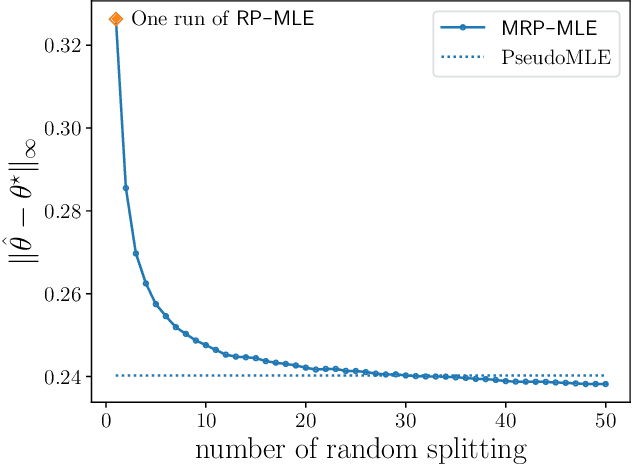
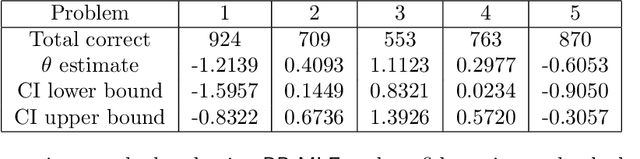
The Rasch model, a classical model in the item response theory, is widely used in psychometrics to model the relationship between individuals' latent traits and their binary responses on assessments or questionnaires. In this paper, we introduce a new likelihood-based estimator -- random pairing maximum likelihood estimator ($\mathsf{RP\text{-}MLE}$) and its bootstrapped variant multiple random pairing MLE ($\mathsf{MRP\text{-}MLE}$) that faithfully estimate the item parameters in the Rasch model. The new estimators have several appealing features compared to existing ones. First, both work for sparse observations, an increasingly important scenario in the big data era. Second, both estimators are provably minimax optimal in terms of finite sample $\ell_{\infty}$ estimation error. Lastly, $\mathsf{RP\text{-}MLE}$ admits precise distributional characterization that allows uncertainty quantification on the item parameters, e.g., construction of confidence intervals of the item parameters. The main idea underlying $\mathsf{RP\text{-}MLE}$ and $\mathsf{MRP\text{-}MLE}$ is to randomly pair user-item responses to form item-item comparisons. This is carefully designed to reduce the problem size while retaining statistical independence. We also provide empirical evidence of the efficacy of the two new estimators using both simulated and real data.

Top-$K$ ranking with a monotone adversary

In this paper, we address the top-$K$ ranking problem with a monotone adversary. We consider the scenario where a comparison graph is randomly generated and the adversary is allowed to add arbitrary edges. The statistician's goal is then to accurately identify the top-$K$ preferred items based on pairwise comparisons derived from this semi-random comparison graph. The main contribution of this paper is to develop a weighted maximum likelihood estimator (MLE) that achieves near-optimal sample complexity, up to a $\log^2(n)$ factor, where n denotes the number of items under comparison. This is made possible through a combination of analytical and algorithmic innovations. On the analytical front, we provide a refined $\ell_\infty$ error analysis of the weighted MLE that is more explicit and tighter than existing analyses. It relates the $\ell_\infty$ error with the spectral properties of the weighted comparison graph. Motivated by this, our algorithmic innovation involves the development of an SDP-based approach to reweight the semi-random graph and meet specified spectral properties. Additionally, we propose a first-order method based on the Matrix Multiplicative Weight Update (MMWU) framework. This method efficiently solves the resulting SDP in nearly-linear time relative to the size of the semi-random comparison graph.

$O(T^{-1})$ Convergence of Optimistic-Follow-the-Regularized-Leader in Two-Player Zero-Sum Markov Games

We prove that optimistic-follow-the-regularized-leader (OFTRL), together with smooth value updates, finds an $O(T^{-1})$-approximate Nash equilibrium in $T$ iterations for two-player zero-sum Markov games with full information. This improves the $\tilde{O}(T^{-5/6})$ convergence rate recently shown in the paper Zhang et al (2022). The refined analysis hinges on two essential ingredients. First, the sum of the regrets of the two players, though not necessarily non-negative as in normal-form games, is approximately non-negative in Markov games. This property allows us to bound the second-order path lengths of the learning dynamics. Second, we prove a tighter algebraic inequality regarding the weights deployed by OFTRL that shaves an extra $\log T$ factor. This crucial improvement enables the inductive analysis that leads to the final $O(T^{-1})$ rate.