SPM-Bench: Benchmarking Large Language Models for Scanning Probe Microscopy

As LLMs achieved breakthroughs in general reasoning, their proficiency in specialized scientific domains reveals pronounced gaps in existing benchmarks due to data contamination, insufficient complexity, and prohibitive human labor costs. Here we present SPM-Bench, an original, PhD-level multimodal benchmark specifically designed for scanning probe microscopy (SPM). We propose a fully automated data synthesis pipeline that ensures both high authority and low-cost. By employing Anchor-Gated Sieve (AGS) technology, we efficiently extract high-value image-text pairs from arXiv and journal papers published between 2023 and 2025. Through a hybrid cloud-local architecture where VLMs return only spatial coordinates "llbox" for local high-fidelity cropping, our pipeline achieves extreme token savings while maintaining high dataset purity. To accurately and objectively evaluate the performance of the LLMs, we introduce the Strict Imperfection Penalty F1 (SIP-F1) score. This metric not only establishes a rigorous capability hierarchy but also, for the first time, quantifies model "personalities" (Conservative, Aggressive, Gambler, or Wise). By correlating these results with model-reported confidence and perceived difficulty, we expose the true reasoning boundaries of current AI in complex physical scenarios. These insights establish SPM-Bench as a generalizable paradigm for automated scientific data synthesis.

HLE-Verified: A Systematic Verification and Structured Revision of Humanity's Last Exam

Humanity's Last Exam (HLE) has become a widely used benchmark for evaluating frontier large language models on challenging, multi-domain questions. However, community-led analyses have raised concerns that HLE contains a non-trivial number of noisy items, which can bias evaluation results and distort cross-model comparisons. To address this challenge, we introduce HLE-Verified, a verified and revised version of HLE with a transparent verification protocol and fine-grained error taxonomy. Our construction follows a two-stage validation-and-repair workflow resulting in a certified benchmark. In Stage I, each item undergoes binary validation of the problem and final answer through domain-expert review and model-based cross-checks, yielding 641 verified items. In Stage II, flawed but fixable items are revised under strict constraints preserving the original evaluation intent, through dual independent expert repairs, model-assisted auditing, and final adjudication, resulting in 1,170 revised-and-certified items. The remaining 689 items are released as a documented uncertain set with explicit uncertainty sources and expertise tags for future refinement. We evaluate seven state-of-the-art language models on HLE and HLE-Verified, observing an average absolute accuracy gain of 7--10 percentage points on HLE-Verified. The improvement is particularly pronounced on items where the original problem statement and/or reference answer is erroneous, with gains of 30--40 percentage points. Our analyses further reveal a strong association between model confidence and the presence of errors in the problem statement or reference answer, supporting the effectiveness of our revisions. Overall, HLE-Verified improves HLE-style evaluations by reducing annotation noise and enabling more faithful measurement of model capabilities. Data is available at: https://github.com/SKYLENAGE-AI/HLE-Verified

DeepMTL2R: A Library for Deep Multi-task Learning to Rank

This paper presents DeepMTL2R, an open-source deep learning framework for Multi-task Learning to Rank (MTL2R), where multiple relevance criteria must be optimized simultaneously. DeepMTL2R integrates heterogeneous relevance signals into a unified, context-aware model by leveraging the self-attention mechanism of transformer architectures, enabling effective learning across diverse and potentially conflicting objectives. The framework includes 21 state-of-the-art multi-task learning algorithms and supports multi-objective optimization to identify Pareto-optimal ranking models. By capturing complex dependencies and long-range interactions among items and labels, DeepMTL2R provides a scalable and expressive solution for modern ranking systems and facilitates controlled comparisons across MTL strategies. We demonstrate its effectiveness on a publicly available dataset, report competitive performance, and visualize the resulting trade-offs among objectives. DeepMTL2R is available at \href{https://github.com/amazon-science/DeepMTL2R}{https://github.com/amazon-science/DeepMTL2R}.

Scalable Bilevel Loss Balancing for Multi-Task Learning

Multi-task learning (MTL) has been widely adopted for its ability to simultaneously learn multiple tasks. While existing gradient manipulation methods often yield more balanced solutions than simple scalarization-based approaches, they typically incur a significant computational overhead of $\mathcal{O}(K)$ in both time and memory, where $K$ is the number of tasks. In this paper, we propose BiLB4MTL, a simple and scalable loss balancing approach for MTL, formulated from a novel bilevel optimization perspective. Our method incorporates three key components: (i) an initial loss normalization, (ii) a bilevel loss-balancing formulation, and (iii) a scalable first-order algorithm that requires only $\mathcal{O}(1)$ time and memory. Theoretically, we prove that BiLB4MTL guarantees convergence not only to a stationary point of the bilevel loss balancing problem but also to an $\epsilon$-accurate Pareto stationary point for all $K$ loss functions under mild conditions. Extensive experiments on diverse multi-task datasets demonstrate that BiLB4MTL achieves state-of-the-art performance in both accuracy and efficiency. Code is available at https://github.com/OptMN-Lab/-BiLB4MTL.

ReGNet: Reciprocal Space-Aware Long-Range Modeling and Multi-Property Prediction for Crystals

Predicting properties of crystals from their structures is a fundamental yet challenging task in materials science. Unlike molecules, crystal structures exhibit infinite periodic arrangements of atoms, requiring methods capable of capturing both local and global information effectively. However, most current works fall short of capturing long-range interactions within periodic structures. To address this limitation, we leverage reciprocal space to efficiently encode long-range interactions with learnable filters within Fourier transforms. We introduce Reciprocal Geometry Network (ReGNet), a novel architecture that integrates geometric GNNs and reciprocal blocks to model short-range and long-range interactions, respectively. Additionally, we introduce ReGNet-MT, a multi-task extension that employs mixture of experts (MoE) for multi-property prediction. Experimental results on the JARVIS and Materials Project benchmarks demonstrate that ReGNet achieves significant performance improvements. Moreover, ReGNet-MT attains state-of-the-art results on two bandgap properties due to positive transfer, while maintaining high computational efficiency. These findings highlight the potential of our model as a scalable and accurate solution for crystal property prediction. The code will be released upon paper acceptance.

On the Convergence of Multi-objective Optimization under Generalized Smoothness

Multi-objective optimization (MOO) is receiving more attention in various fields such as multi-task learning. Recent works provide some effective algorithms with theoretical analysis but they are limited by the standard $L$-smooth or bounded-gradient assumptions, which are typically unsatisfactory for neural networks, such as recurrent neural networks (RNNs) and transformers. In this paper, we study a more general and realistic class of $\ell$-smooth loss functions, where $\ell$ is a general non-decreasing function of gradient norm. We develop two novel single-loop algorithms for $\ell$-smooth MOO problems, Generalized Smooth Multi-objective Gradient descent (GSMGrad) and its stochastic variant, Stochastic Generalized Smooth Multi-objective Gradient descent (SGSMGrad), which approximate the conflict-avoidant (CA) direction that maximizes the minimum improvement among objectives. We provide a comprehensive convergence analysis of both algorithms and show that they converge to an $\epsilon$-accurate Pareto stationary point with a guaranteed $\epsilon$-level average CA distance (i.e., the gap between the updating direction and the CA direction) over all iterations, where totally $\mathcal{O}(\epsilon^{-2})$ and $\mathcal{O}(\epsilon^{-4})$ samples are needed for deterministic and stochastic settings, respectively. Our algorithms can also guarantee a tighter $\epsilon$-level CA distance in each iteration using more samples. Moreover, we propose a practical variant of GSMGrad named GSMGrad-FA using only constant-level time and space, while achieving the same performance guarantee as GSMGrad. Our experiments validate our theory and demonstrate the effectiveness of the proposed methods.

Finite-Time Analysis for Conflict-Avoidant Multi-Task Reinforcement Learning

Multi-task reinforcement learning (MTRL) has shown great promise in many real-world applications. Existing MTRL algorithms often aim to learn a policy that optimizes individual objective functions simultaneously with a given prior preference (or weights) on different tasks. However, these methods often suffer from the issue of \textit{gradient conflict} such that the tasks with larger gradients dominate the update direction, resulting in a performance degeneration on other tasks. In this paper, we develop a novel dynamic weighting multi-task actor-critic algorithm (MTAC) under two options of sub-procedures named as CA and FC in task weight updates. MTAC-CA aims to find a conflict-avoidant (CA) update direction that maximizes the minimum value improvement among tasks, and MTAC-FC targets at a much faster convergence rate. We provide a comprehensive finite-time convergence analysis for both algorithms. We show that MTAC-CA can find a $\epsilon+\epsilon_{\text{app}}$-accurate Pareto stationary policy using $\mathcal{O}({\epsilon^{-5}})$ samples, while ensuring a small $\epsilon+\sqrt{\epsilon_{\text{app}}}$-level CA distance (defined as the distance to the CA direction), where $\epsilon_{\text{app}}$ is the function approximation error. The analysis also shows that MTAC-FC improves the sample complexity to $\mathcal{O}(\epsilon^{-3})$, but with a constant-level CA distance. Our experiments on MT10 demonstrate the improved performance of our algorithms over existing MTRL methods with fixed preference.

Achieving ${O}(ε^{-1.5})$ Complexity in Hessian/Jacobian-free Stochastic Bilevel Optimization

In this paper, we revisit the bilevel optimization problem, in which the upper-level objective function is generally nonconvex and the lower-level objective function is strongly convex. Although this type of problem has been studied extensively, it still remains an open question how to achieve an ${O}(\epsilon^{-1.5})$ sample complexity in Hessian/Jacobian-free stochastic bilevel optimization without any second-order derivative computation. To fill this gap, we propose a novel Hessian/Jacobian-free bilevel optimizer named FdeHBO, which features a simple fully single-loop structure, a projection-aided finite-difference Hessian/Jacobian-vector approximation, and momentum-based updates. Theoretically, we show that FdeHBO requires ${O}(\epsilon^{-1.5})$ iterations (each using ${O}(1)$ samples and only first-order gradient information) to find an $\epsilon$-accurate stationary point. As far as we know, this is the first Hessian/Jacobian-free method with an ${O}(\epsilon^{-1.5})$ sample complexity for nonconvex-strongly-convex stochastic bilevel optimization.

SimFBO: Towards Simple, Flexible and Communication-efficient Federated Bilevel Learning

Federated bilevel optimization (FBO) has shown great potential recently in machine learning and edge computing due to the emerging nested optimization structure in meta-learning, fine-tuning, hyperparameter tuning, etc. However, existing FBO algorithms often involve complicated computations and require multiple sub-loops per iteration, each of which contains a number of communication rounds. In this paper, we propose a simple and flexible FBO framework named SimFBO, which is easy to implement without sub-loops, and includes a generalized server-side aggregation and update for improving communication efficiency. We further propose System-level heterogeneity robust FBO (ShroFBO) as a variant of SimFBO with stronger resilience to heterogeneous local computation. We show that SimFBO and ShroFBO provably achieve a linear convergence speedup with partial client participation and client sampling without replacement, as well as improved sample and communication complexities. Experiments demonstrate the effectiveness of the proposed methods over existing FBO algorithms.

Direction-oriented Multi-objective Learning: Simple and Provable Stochastic Algorithms

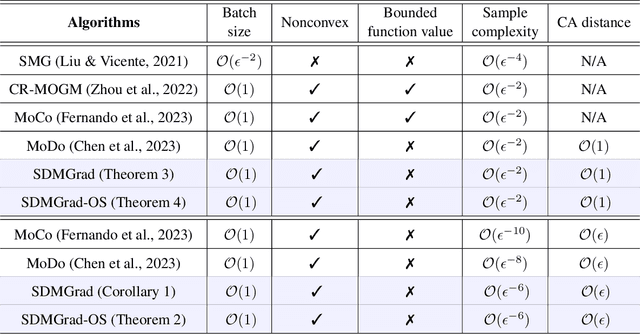
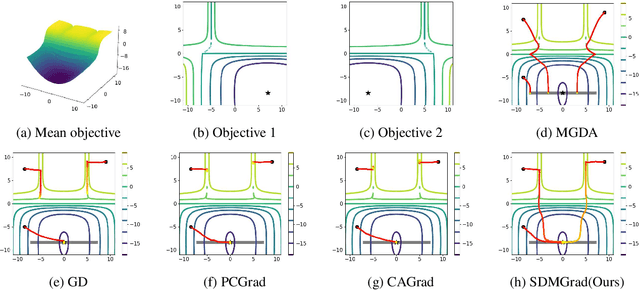
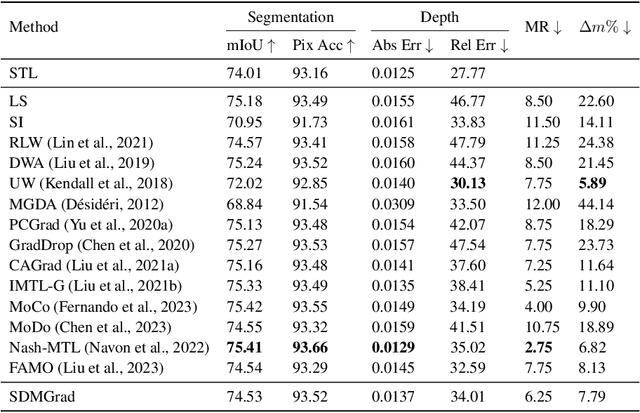
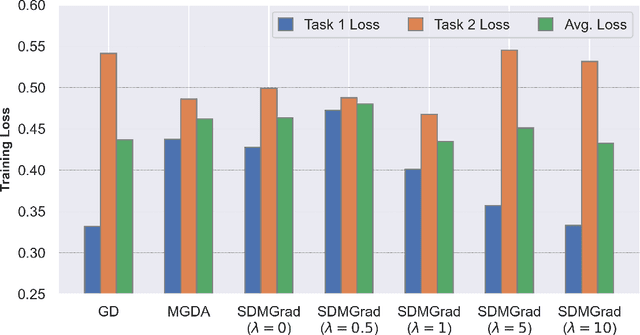
Multi-objective optimization (MOO) has become an influential framework in many machine learning problems with multiple objectives such as learning with multiple criteria and multi-task learning (MTL). In this paper, we propose a new direction-oriented multi-objective problem by regularizing the common descent direction within a neighborhood of a direction that optimizes a linear combination of objectives such as the average loss in MTL. This formulation includes GD and MGDA as special cases, enjoys the direction-oriented benefit as in CAGrad, and facilitates the design of stochastic algorithms. To solve this problem, we propose Stochastic Direction-oriented Multi-objective Gradient descent (SDMGrad) with simple SGD type of updates, and its variant SDMGrad-OS with an efficient objective sampling in the setting where the number of objectives is large. For a constant-level regularization parameter $\lambda$, we show that SDMGrad and SDMGrad-OS provably converge to a Pareto stationary point with improved complexities and milder assumptions. For an increasing $\lambda$, this convergent point reduces to a stationary point of the linear combination of objectives. We demonstrate the superior performance of the proposed methods in a series of tasks on multi-task supervised learning and reinforcement learning. Code is provided at https://github.com/ml-opt-lab/sdmgrad.