Non-Asymptotic Analysis for Single-Loop Actor-Critic with Compatible Function Approximation

Actor-critic (AC) is a powerful method for learning an optimal policy in reinforcement learning, where the critic uses algorithms, e.g., temporal difference (TD) learning with function approximation, to evaluate the current policy and the actor updates the policy along an approximate gradient direction using information from the critic. This paper provides the \textit{tightest} non-asymptotic convergence bounds for both the AC and natural AC (NAC) algorithms. Specifically, existing studies show that AC converges to an $\epsilon+\varepsilon_{\text{critic}}$ neighborhood of stationary points with the best known sample complexity of $\mathcal{O}(\epsilon^{-2})$ (up to a log factor), and NAC converges to an $\epsilon+\varepsilon_{\text{critic}}+\sqrt{\varepsilon_{\text{actor}}}$ neighborhood of the global optimum with the best known sample complexity of $\mathcal{O}(\epsilon^{-3})$, where $\varepsilon_{\text{critic}}$ is the approximation error of the critic and $\varepsilon_{\text{actor}}$ is the approximation error induced by the insufficient expressive power of the parameterized policy class. This paper analyzes the convergence of both AC and NAC algorithms with compatible function approximation. Our analysis eliminates the term $\varepsilon_{\text{critic}}$ from the error bounds while still achieving the best known sample complexities. Moreover, we focus on the challenging single-loop setting with a single Markovian sample trajectory. Our major technical novelty lies in analyzing the stochastic bias due to policy-dependent and time-varying compatible function approximation in the critic, and handling the non-ergodicity of the MDP due to the single Markovian sample trajectory. Numerical results are also provided in the appendix.

Finite-Time Analysis for Conflict-Avoidant Multi-Task Reinforcement Learning

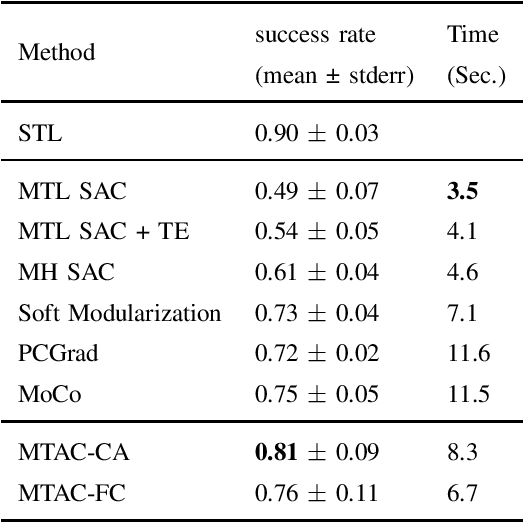
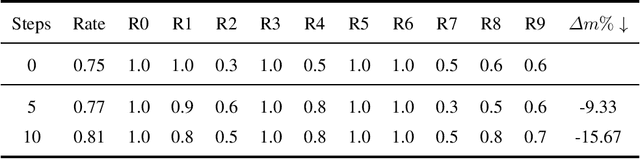
Multi-task reinforcement learning (MTRL) has shown great promise in many real-world applications. Existing MTRL algorithms often aim to learn a policy that optimizes individual objective functions simultaneously with a given prior preference (or weights) on different tasks. However, these methods often suffer from the issue of \textit{gradient conflict} such that the tasks with larger gradients dominate the update direction, resulting in a performance degeneration on other tasks. In this paper, we develop a novel dynamic weighting multi-task actor-critic algorithm (MTAC) under two options of sub-procedures named as CA and FC in task weight updates. MTAC-CA aims to find a conflict-avoidant (CA) update direction that maximizes the minimum value improvement among tasks, and MTAC-FC targets at a much faster convergence rate. We provide a comprehensive finite-time convergence analysis for both algorithms. We show that MTAC-CA can find a $\epsilon+\epsilon_{\text{app}}$-accurate Pareto stationary policy using $\mathcal{O}({\epsilon^{-5}})$ samples, while ensuring a small $\epsilon+\sqrt{\epsilon_{\text{app}}}$-level CA distance (defined as the distance to the CA direction), where $\epsilon_{\text{app}}$ is the function approximation error. The analysis also shows that MTAC-FC improves the sample complexity to $\mathcal{O}(\epsilon^{-3})$, but with a constant-level CA distance. Our experiments on MT10 demonstrate the improved performance of our algorithms over existing MTRL methods with fixed preference.

Transgender Community Sentiment Analysis from Social Media Data: A Natural Language Processing Approach

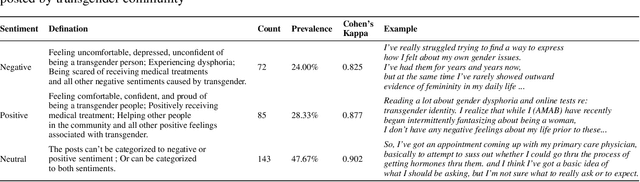
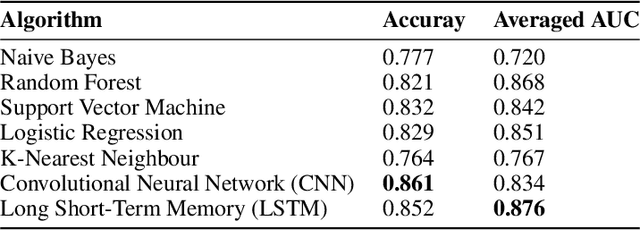
Transgender community is experiencing a huge disparity in mental health conditions compared with the general population. Interpreting the social medial data posted by transgender people may help us understand the sentiments of these sexual minority groups better and apply early interventions. In this study, we manually categorize 300 social media comments posted by transgender people to the sentiment of negative, positive, and neutral. 5 machine learning algorithms and 2 deep neural networks are adopted to build sentiment analysis classifiers based on the annotated data. Results show that our annotations are reliable with a high Cohen's Kappa score over 0.8 across all three classes. LSTM model yields an optimal performance of accuracy over 0.85 and AUC of 0.876. Our next step will focus on using advanced natural language processing algorithms on a larger annotated dataset.