Variational Neural Stochastic Differential Equations with Change Points

In this work, we explore modeling change points in time-series data using neural stochastic differential equations (neural SDEs). We propose a novel model formulation and training procedure based on the variational autoencoder (VAE) framework for modeling time-series as a neural SDE. Unlike existing algorithms training neural SDEs as VAEs, our proposed algorithm only necessitates a Gaussian prior of the initial state of the latent stochastic process, rather than a Wiener process prior on the entire latent stochastic process. We develop two methodologies for modeling and estimating change points in time-series data with distribution shifts. Our iterative algorithm alternates between updating neural SDE parameters and updating the change points based on either a maximum likelihood-based approach or a change point detection algorithm using the sequential likelihood ratio test. We provide a theoretical analysis of this proposed change point detection scheme. Finally, we present an empirical evaluation that demonstrates the expressive power of our proposed model, showing that it can effectively model both classical parametric SDEs and some real datasets with distribution shifts.

Constrained Reinforcement Learning Under Model Mismatch

Existing studies on constrained reinforcement learning (RL) may obtain a well-performing policy in the training environment. However, when deployed in a real environment, it may easily violate constraints that were originally satisfied during training because there might be model mismatch between the training and real environments. To address the above challenge, we formulate the problem as constrained RL under model uncertainty, where the goal is to learn a good policy that optimizes the reward and at the same time satisfy the constraint under model mismatch. We develop a Robust Constrained Policy Optimization (RCPO) algorithm, which is the first algorithm that applies to large/continuous state space and has theoretical guarantees on worst-case reward improvement and constraint violation at each iteration during the training. We demonstrate the effectiveness of our algorithm on a set of RL tasks with constraints.

Neural Stochastic Differential Equations with Change Points: A Generative Adversarial Approach

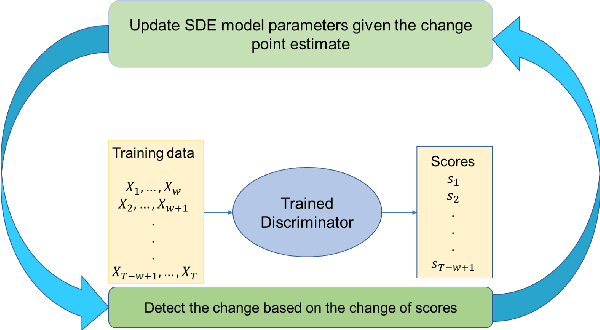
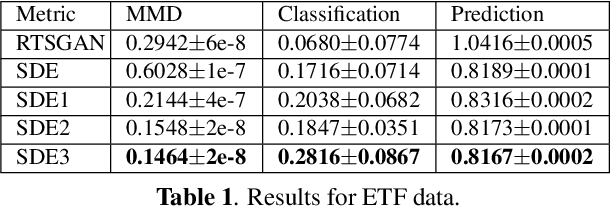
Stochastic differential equations (SDEs) have been widely used to model real world random phenomena. Existing works mainly focus on the case where the time series is modeled by a single SDE, which might be restrictive for modeling time series with distributional shift. In this work, we propose a change point detection algorithm for time series modeled as neural SDEs. Given a time series dataset, the proposed method jointly learns the unknown change points and the parameters of distinct neural SDE models corresponding to each change point. Specifically, the SDEs are learned under the framework of generative adversarial networks (GANs) and the change points are detected based on the output of the GAN discriminator in a forward pass. At each step of the proposed algorithm, the change points and the SDE model parameters are updated in an alternating fashion. Numerical results on both synthetic and real datasets are provided to validate the performance of our algorithm in comparison to classical change point detection benchmarks, standard GAN-based neural SDEs, and other state-of-the-art deep generative models for time series data.

Quickest Change Detection in Autoregressive Models

The problem of quickest change detection (QCD) in autoregressive (AR) models is investigated. A system is being monitored with sequentially observed samples. At some unknown time, a disturbance signal occurs and changes the distribution of the observations. The disturbance signal follows an AR model, which is dependent over time. Before the change, observations only consist of measurement noise, and are independent and identically distributed (i.i.d.). After the change, observations consist of the disturbance signal and the measurement noise, are dependent over time, which essentially follow a continuous-state hidden Markov model (HMM). The goal is to design a stopping time to detect the disturbance signal as quickly as possible subject to false alarm constraints. Existing approaches for general non-i.i.d. settings and discrete-state HMMs cannot be applied due to their high computational complexity and memory consumption, and they usually assume some asymptotic stability condition. In this paper, the asymptotic stability condition is firstly theoretically proved for the AR model by a novel design of forward variable and auxiliary Markov chain. A computationally efficient Ergodic CuSum algorithm that can be updated recursively is then constructed and is further shown to be asymptotically optimal. The data-driven setting where the disturbance signal parameters are unknown is further investigated, and an online and computationally efficient gradient ascent CuSum algorithm is designed. The algorithm is constructed by iteratively updating the estimate of the unknown parameters based on the maximum likelihood principle and the gradient ascent approach. The lower bound on its average running length to false alarm is also derived for practical false alarm control. Simulation results are provided to demonstrate the performance of the proposed algorithms.

Quickest Anomaly Detection in Sensor Networks With Unlabeled Samples

The problem of quickest anomaly detection in networks with unlabeled samples is studied. At some unknown time, an anomaly emerges in the network and changes the data-generating distribution of some unknown sensor. The data vector received by the fusion center at each time step undergoes some unknown and arbitrary permutation of its entries (unlabeled samples). The goal of the fusion center is to detect the anomaly with minimal detection delay subject to false alarm constraints. With unlabeled samples, existing approaches that combines local cumulative sum (CuSum) statistics cannot be used anymore. Several major questions include whether detection is still possible without the label information, if so, what is the fundamental limit and how to achieve that. Two cases with static and dynamic anomaly are investigated, where the sensor affected by the anomaly may or may not change with time. For the two cases, practical algorithms based on the ideas of mixture likelihood ratio and/or maximum likelihood estimate are constructed. Their average detection delays and false alarm rates are theoretically characterized. Universal lower bounds on the average detection delay for a given false alarm rate are also derived, which further demonstrate the asymptotic optimality of the two algorithms.

Kernel Robust Hypothesis Testing

The problem of robust hypothesis testing is studied, where under the null and the alternative hypotheses, the data-generating distributions are assumed to be in some uncertainty sets, and the goal is to design a test that performs well under the worst-case distributions over the uncertainty sets. In this paper, uncertainty sets are constructed in a data-driven manner using kernel method, i.e., they are centered around empirical distributions of training samples from the null and alternative hypotheses, respectively; and are constrained via the distance between kernel mean embeddings of distributions in the reproducing kernel Hilbert space, i.e., maximum mean discrepancy (MMD). The Bayesian setting and the Neyman-Pearson setting are investigated. For the Bayesian setting where the goal is to minimize the worst-case error probability, an optimal test is firstly obtained when the alphabet is finite. When the alphabet is infinite, a tractable approximation is proposed to quantify the worst-case average error probability, and a kernel smoothing method is further applied to design test that generalizes to unseen samples. A direct robust kernel test is also proposed and proved to be exponentially consistent. For the Neyman-Pearson setting, where the goal is to minimize the worst-case probability of miss detection subject to a constraint on the worst-case probability of false alarm, an efficient robust kernel test is proposed and is shown to be asymptotically optimal. Numerical results are provided to demonstrate the performance of the proposed robust tests.

Quickest Change Detection in Anonymous Heterogeneous Sensor Networks

The problem of quickest change detection (QCD) in anonymous heterogeneous sensor networks is studied. There are $n$ heterogeneous sensors and a fusion center. The sensors are clustered into $K$ groups, and different groups follow different data-generating distributions. At some unknown time, an event occurs in the network and changes the data-generating distribution of the sensors. The goal is to detect the change as quickly as possible, subject to false alarm constraints. The anonymous setting is studied, where at each time step, the fusion center receives $n$ unordered samples, and the fusion center does not know which sensor each sample comes from, and thus does not know its exact distribution. A simple optimality proof is first derived for the mixture likelihood ratio test, which was constructed and proved to be optimal for the non-sequential anonymous setting in (Chen and Wang, 2019). For the QCD problem, a mixture CuSum algorithm is further constructed, and is further shown to be optimal under Lorden's criterion. For large networks, a computationally efficient test is proposed and a novel theoretical characterization of its false alarm rate is developed. Numerical results are provided to validate the theoretical results.