Neural Stochastic Differential Equations with Change Points: A Generative Adversarial Approach
Paper and Code
Dec 20, 2023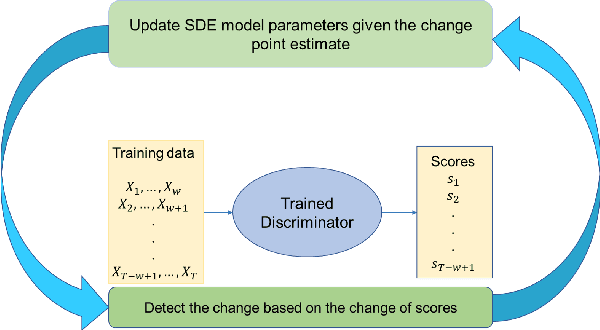
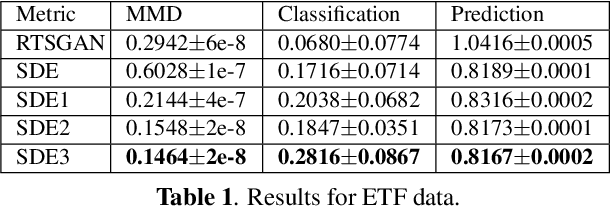

Stochastic differential equations (SDEs) have been widely used to model real world random phenomena. Existing works mainly focus on the case where the time series is modeled by a single SDE, which might be restrictive for modeling time series with distributional shift. In this work, we propose a change point detection algorithm for time series modeled as neural SDEs. Given a time series dataset, the proposed method jointly learns the unknown change points and the parameters of distinct neural SDE models corresponding to each change point. Specifically, the SDEs are learned under the framework of generative adversarial networks (GANs) and the change points are detected based on the output of the GAN discriminator in a forward pass. At each step of the proposed algorithm, the change points and the SDE model parameters are updated in an alternating fashion. Numerical results on both synthetic and real datasets are provided to validate the performance of our algorithm in comparison to classical change point detection benchmarks, standard GAN-based neural SDEs, and other state-of-the-art deep generative models for time series data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge