Path Planning for Multiple Heterogeneous Unmanned Vehicles with Uncertain Service Times
Paper and Code
Feb 24, 2017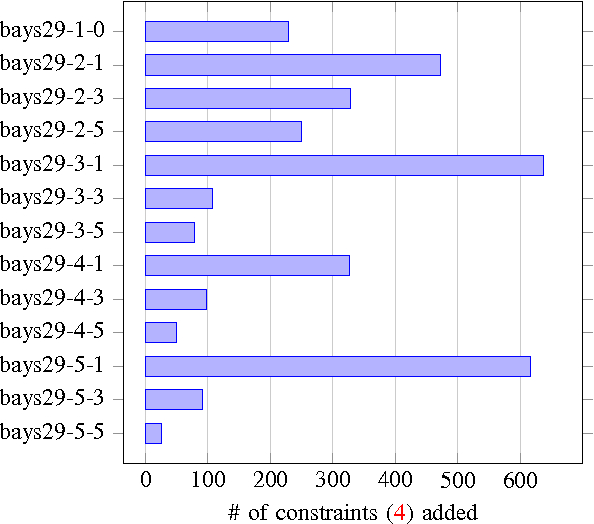
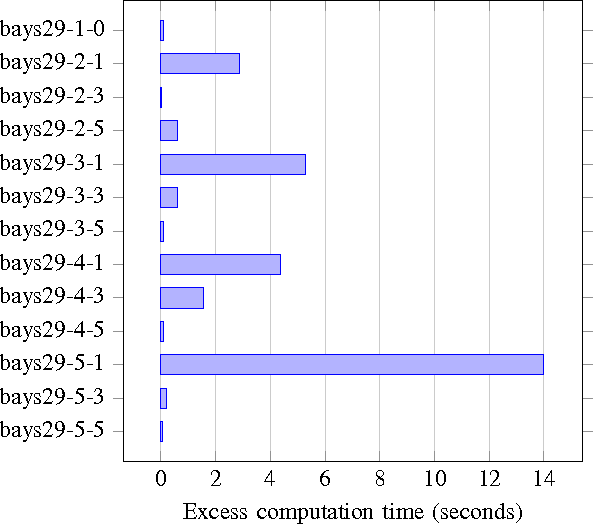
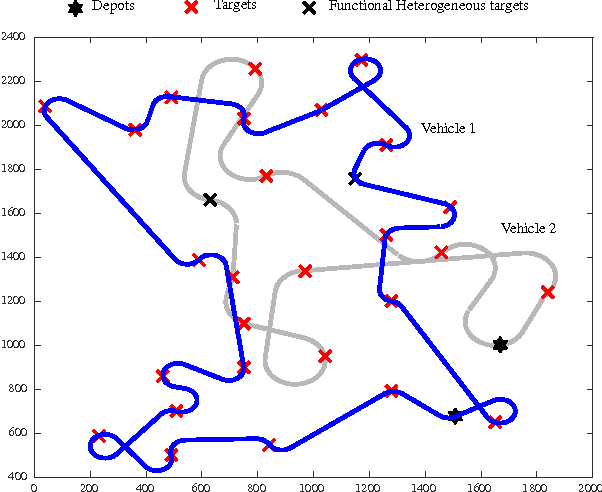
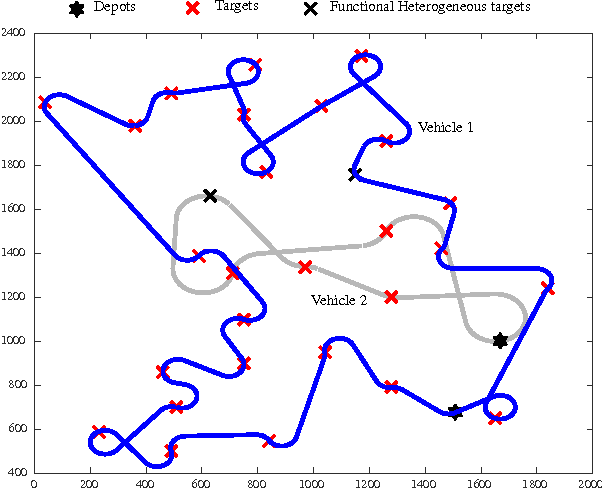
This article presents a framework and develops a formulation to solve a path planning problem for multiple heterogeneous Unmanned Vehicles (UVs) with uncertain service times for each vehicle--target pair. The vehicles incur a penalty proportional to the duration of their total service time in excess of a preset constant. The vehicles differ in their motion constraints and are located at distinct depots at the start of the mission. The vehicles may also be equipped with disparate sensors. The objective is to find a tour for each vehicle that starts and ends at its respective depot such that every target is visited and serviced by some vehicle while minimizing the sum of the total travel distance and the expected penalty incurred by all the vehicles. We formulate the problem as a two-stage stochastic program with recourse, present the theoretical properties of the formulation and advantages of using such a formulation, as opposed to a deterministic expected value formulation, to solve the problem. Extensive numerical simulations also corroborate the effectiveness of the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge