Power Flow Approximations for Multiphase Distribution Networks using Gaussian Processes

Learning-based approaches are increasingly leveraged to manage and coordinate the operation of grid-edge resources in active power distribution networks. Among these, model-based techniques stand out for their superior data efficiency and robustness compared to model-free methods. However, effective model learning requires a learning-based approximator for the underlying power flow model. This study extends existing work by introducing a data-driven power flow method based on Gaussian Processes (GPs) to approximate the multiphase power flow model, by mapping net load injections to nodal voltages. Simulation results using the IEEE 123-bus and 8500-node distribution test feeders demonstrate that the trained GP model can reliably predict the nonlinear power flow solutions with minimal training data. We also conduct a comparative analysis of the training efficiency and testing performance of the proposed GP-based power flow approximator against a deep neural network-based approximator, highlighting the advantages of our data-efficient approach. Results over realistic operating conditions show that despite an 85% reduction in the training sample size (corresponding to a 92.8% improvement in training time), GP models produce a 99.9% relative reduction in mean absolute error compared to the baselines of deep neural networks.

Optimization Proxies using Limited Labeled Data and Training Time -- A Semi-Supervised Bayesian Neural Network Approach

Constrained optimization problems arise in various engineering system operations such as inventory management and electric power grids. However, the requirement to repeatedly solve such optimization problems with uncertain parameters poses a significant computational challenge. This work introduces a learning scheme using Bayesian Neural Networks (BNNs) to solve constrained optimization problems under limited labeled data and restricted model training times. We propose a semi-supervised BNN for this practical but complex regime, wherein training commences in a sandwiched fashion, alternating between a supervised learning step (using labeled data) for minimizing cost, and an unsupervised learning step (using unlabeled data) for enforcing constraint feasibility. Both supervised and unsupervised steps use a Bayesian approach, where Stochastic Variational Inference is employed for approximate Bayesian inference. We show that the proposed semi-supervised learning method outperforms conventional BNN and deep neural network (DNN) architectures on important non-convex constrained optimization problems from energy network operations, achieving up to a tenfold reduction in expected maximum equality gap and halving the optimality and inequality (feasibility) gaps, without requiring any correction or projection step. By leveraging the BNN's ability to provide posterior samples at minimal computational cost, we demonstrate that a Selection via Posterior (SvP) scheme can further reduce equality gaps by more than 10%. We also provide tight and practically meaningful probabilistic confidence bounds that can be constructed using a low number of labeled testing data and readily adapted to other applications.

Data-Efficient Power Flow Learning for Network Contingencies

This work presents an efficient data-driven method to learn power flows in grids with network contingencies and to estimate corresponding probabilistic voltage envelopes (PVE). First, a network-aware Gaussian process (GP) termed Vertex-Degree Kernel (VDK-GP), developed in prior work, is used to estimate voltage-power functions for a few network configurations. The paper introduces a novel multi-task vertex degree kernel (MT-VDK) that amalgamates the learned VDK-GPs to determine power flows for unseen networks, with a significant reduction in the computational complexity and hyperparameter requirements compared to alternate approaches. Simulations on the IEEE 30-Bus network demonstrate the retention and transfer of power flow knowledge in both N-1 and N-2 contingency scenarios. The MT-VDK-GP approach achieves over 50% reduction in mean prediction error for novel N-1 contingency network configurations in low training data regimes (50-250 samples) over VDK-GP. Additionally, MT-VDK-GP outperforms a hyper-parameter based transfer learning approach in over 75% of N-2 contingency network structures, even without historical N-2 outage data. The proposed method demonstrates the ability to achieve PVEs using sixteen times fewer power flow solutions compared to Monte-Carlo sampling-based methods.

Graph-Structured Kernel Design for Power Flow Learning using Gaussian Processes

This paper presents a physics-inspired graph-structured kernel designed for power flow learning using Gaussian Process (GP). The kernel, named the vertex-degree kernel (VDK), relies on latent decomposition of voltage-injection relationship based on the network graph or topology. Notably, VDK design avoids the need to solve optimization problems for kernel search. To enhance efficiency, we also explore a graph-reduction approach to obtain a VDK representation with lesser terms. Additionally, we propose a novel network-swipe active learning scheme, which intelligently selects sequential training inputs to accelerate the learning of VDK. Leveraging the additive structure of VDK, the active learning algorithm performs a block-descent type procedure on GP's predictive variance, serving as a proxy for information gain. Simulations demonstrate that the proposed VDK-GP achieves more than two fold sample complexity reduction, compared to full GP on medium scale 500-Bus and large scale 1354-Bus power systems. The network-swipe algorithm outperforms mean performance of 500 random trials on test predictions by two fold for medium-sized 500-Bus systems and best performance of 25 random trials for large-scale 1354-Bus systems by 10%. Moreover, we demonstrate that the proposed method's performance for uncertainty quantification applications with distributionally shifted testing data sets.

Gaussian Process Learning-based Probabilistic Optimal Power Flow

In this letter, we present a novel Gaussian Process Learning-based Probabilistic Optimal Power Flow (GP-POPF) for solving POPF under renewable and load uncertainties of arbitrary distribution. The proposed method relies on a non-parametric Bayesian inference-based uncertainty propagation approach, called Gaussian Process (GP). We also suggest a new type of sensitivity called Subspace-wise Sensitivity, using observations on the interpretability of GP-POPF hyperparameters. The simulation results on 14-bus and 30-bus systems show that the proposed method provides reasonably accurate solutions when compared with Monte-Carlo Simulations (MCS) solutions at different levels of uncertain renewable penetration as well as load uncertainties, while requiring much less number of samples and elapsed time.

Non-parametric Probabilistic Load Flow using Gaussian Process Learning

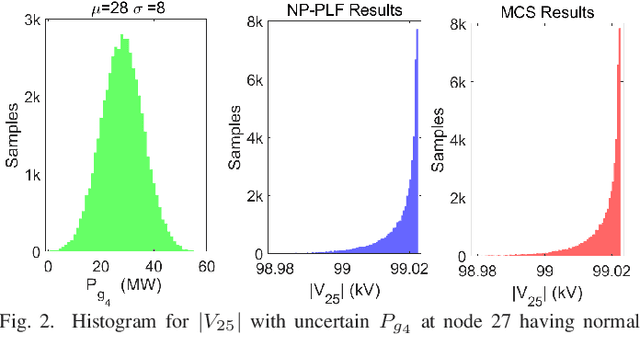
In this paper, we propose a non-parametric probabilistic load flow (NP-PLF) technique based on Gaussian process (GP) learning. The technique can provide "semi-explicit" power flow solutions by implementing learning step and testing step. The proposed NP-PLF leverages upon GP upper confidence bound (GP-UCB) sampling algorithm. The salient features of this NP-PLF method are: i) applicable for power flow problem having power injection uncertainty with unknown class of distribution; ii) providing probabilistic learning bound (PLB) provides control over the error and convergence; iii) capable of handling intermittent distributed generation as well as load uncertainties; and iv) applicable to both balanced and unbalanced power flow with different type and size of systems. The simulation results performed on IEEE 30-bus and IEEE 118-bus system show that the proposed method is able to learn the state variable function in the input subspace using a small number of training samples. Further, the testing with different distributions indicates that more complete statistical information can be obtained on probabilistic power flow problem using the proposed method.