Gaussian Process Learning-based Probabilistic Optimal Power Flow

In this letter, we present a novel Gaussian Process Learning-based Probabilistic Optimal Power Flow (GP-POPF) for solving POPF under renewable and load uncertainties of arbitrary distribution. The proposed method relies on a non-parametric Bayesian inference-based uncertainty propagation approach, called Gaussian Process (GP). We also suggest a new type of sensitivity called Subspace-wise Sensitivity, using observations on the interpretability of GP-POPF hyperparameters. The simulation results on 14-bus and 30-bus systems show that the proposed method provides reasonably accurate solutions when compared with Monte-Carlo Simulations (MCS) solutions at different levels of uncertain renewable penetration as well as load uncertainties, while requiring much less number of samples and elapsed time.

Non-parametric Probabilistic Load Flow using Gaussian Process Learning

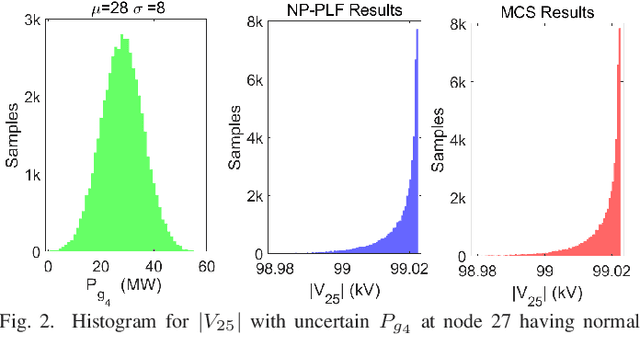
In this paper, we propose a non-parametric probabilistic load flow (NP-PLF) technique based on Gaussian process (GP) learning. The technique can provide "semi-explicit" power flow solutions by implementing learning step and testing step. The proposed NP-PLF leverages upon GP upper confidence bound (GP-UCB) sampling algorithm. The salient features of this NP-PLF method are: i) applicable for power flow problem having power injection uncertainty with unknown class of distribution; ii) providing probabilistic learning bound (PLB) provides control over the error and convergence; iii) capable of handling intermittent distributed generation as well as load uncertainties; and iv) applicable to both balanced and unbalanced power flow with different type and size of systems. The simulation results performed on IEEE 30-bus and IEEE 118-bus system show that the proposed method is able to learn the state variable function in the input subspace using a small number of training samples. Further, the testing with different distributions indicates that more complete statistical information can be obtained on probabilistic power flow problem using the proposed method.

Region of Attraction for Power Systems using Gaussian Process and Converse Lyapunov Function -- Part I: Theoretical Framework and Off-line Study

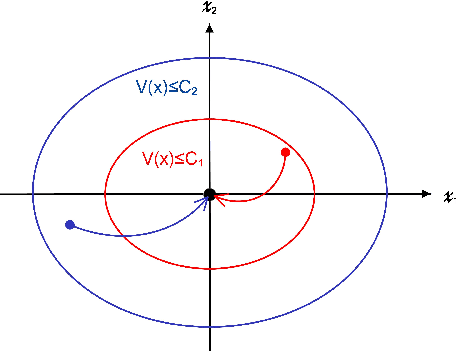
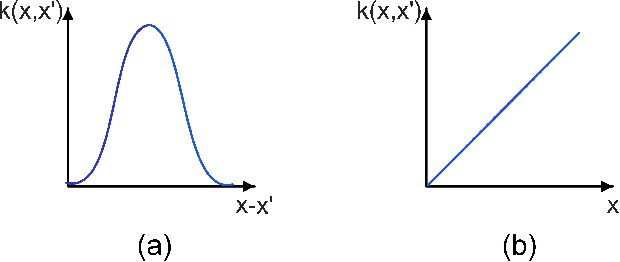
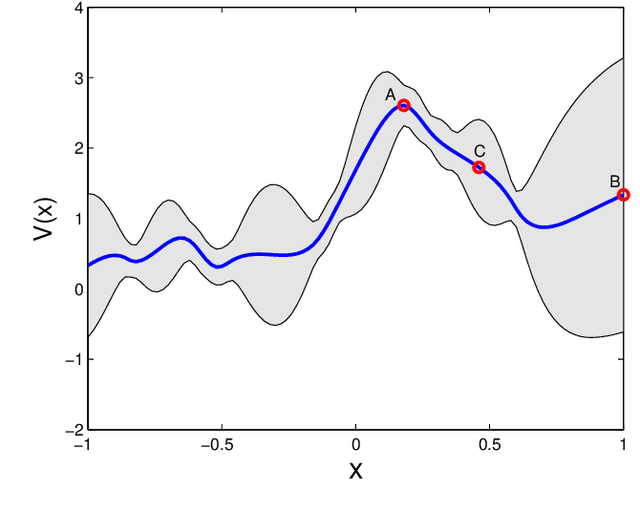
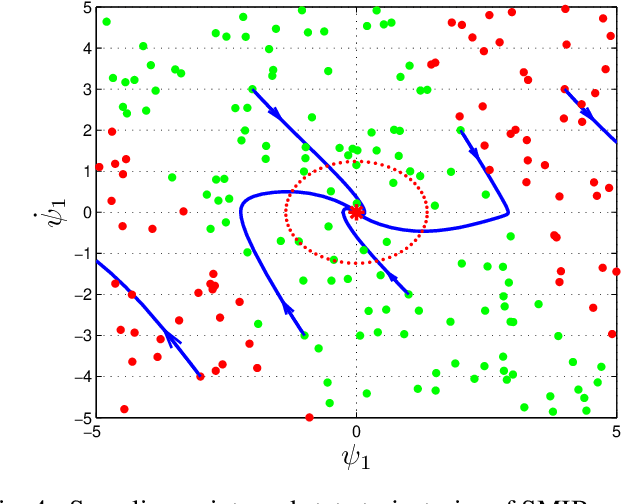
This paper introduces a novel framework to construct the region of attraction (ROA) of a power system centered around a stable equilibrium by using stable state trajectories of system dynamics. Most existing works on estimating ROA rely on analytical Lyapunov functions, which are subject to two limitations: the analytic Lyapunov functions may not be always readily available, and the resulting ROA may be overly conservative. This work overcomes these two limitations by leveraging the converse Lyapunov theorem in control theory to eliminate the need of an analytic Lyapunov function and learning the unknown Lyapunov function with the Gaussian Process (GP) approach. In addition, a Gaussian Process Upper Confidence Bound (GP-UCB) based sampling algorithm is designed to reconcile the trade-off between the exploitation for enlarging the ROA and the exploration for reducing the uncertainty of sampling region. Within the constructed ROA, it is guaranteed in probability that the system state will converge to the stable equilibrium with a confidence level. Numerical simulations are also conducted to validate the assessment approach for the ROA of the single machine infinite bus system and the New England $39$-bus system. Numerical results demonstrate that our approach can significantly enlarge the estimated ROA compared to that of the analytic Lyapunov counterpart.