Chao Zhai
Two-Stage Channel Estimation Approach for Cell-Free IoT With Massive Random Access
Sep 28, 2021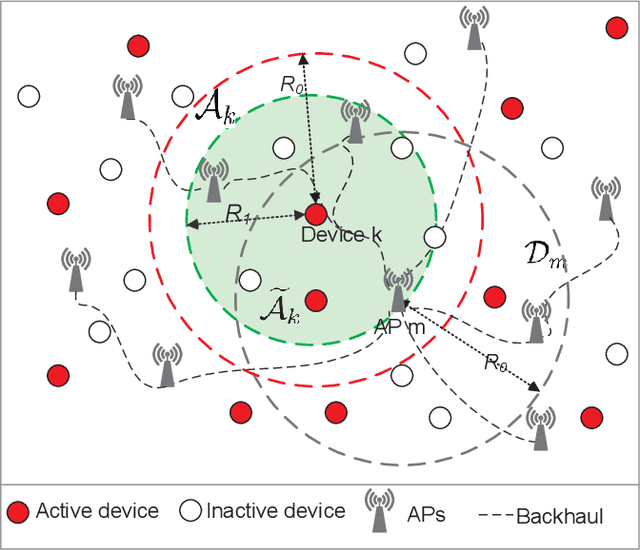
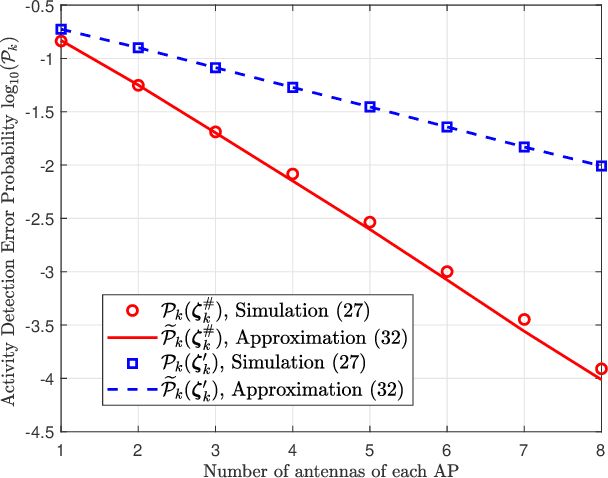
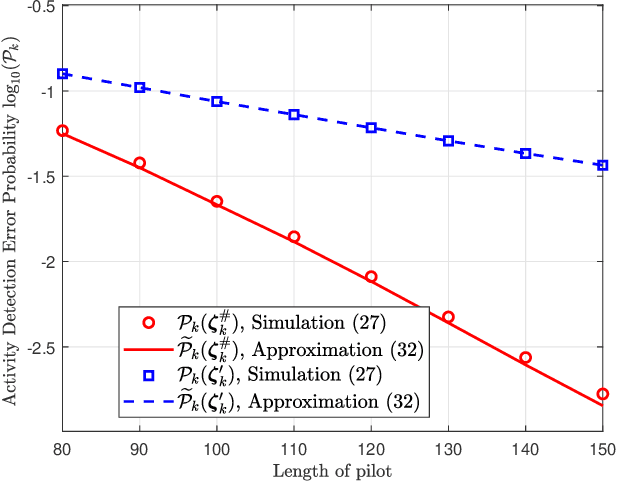
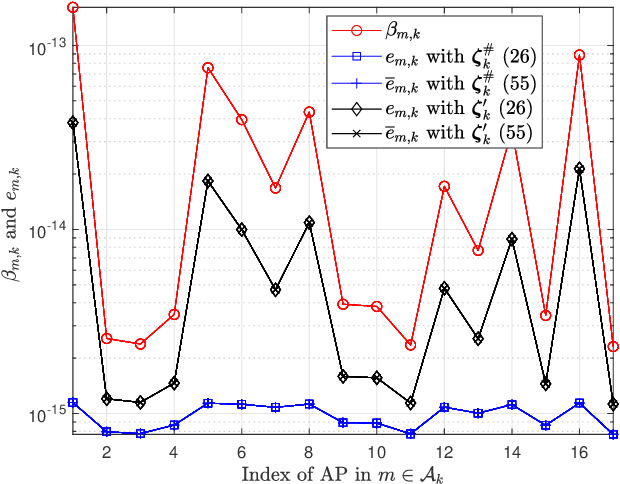
Abstract:We investigate the activity detection and channel estimation issues for cell-free Internet of Things (IoT) networks with massive random access. In each time slot, only partial devices are active and communicate with neighboring access points (APs) using non-orthogonal random pilot sequences. Different from the centralized processing in cellular networks, the activity detection and channel estimation in cell-free IoT is more challenging due to the distributed and user-centric architecture. We propose a two-stage approach to detect the random activities of devices and estimate their channel states. In the first stage, the activity of each device is jointly detected by its adjacent APs based on the vector approximate message passing (Vector AMP) algorithm. In the second stage, each AP re-estimates the channel using the linear minimum mean square error (LMMSE) method based on the detected activities to improve the channel estimation accuracy. We derive closed-form expressions for the activity detection error probability and the mean-squared channel estimation errors for a typical device. Finally, we analyze the performance of the entire cell-free IoT network in terms of coverage probability. Simulation results validate the derived closed-form expressions and show that the cell-free IoT significantly outperforms the collocated massive MIMO and small-cell schemes in terms of coverage probability.
Region of Attraction for Power Systems using Gaussian Process and Converse Lyapunov Function -- Part I: Theoretical Framework and Off-line Study
Jun 09, 2019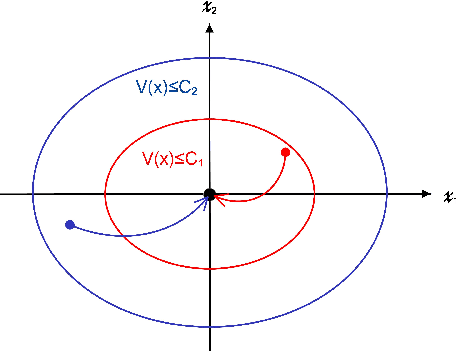
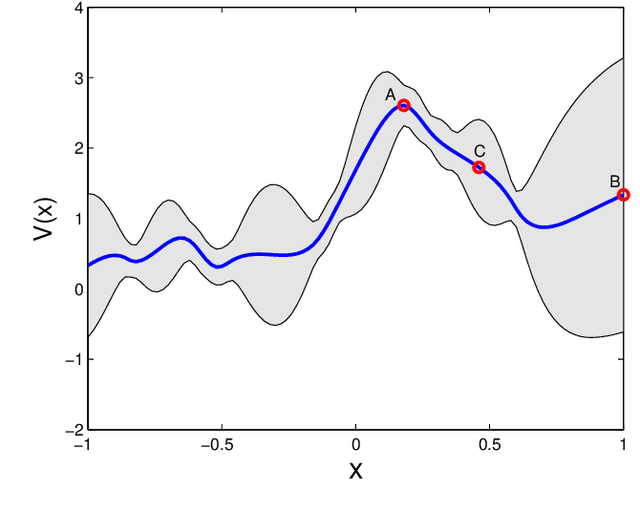
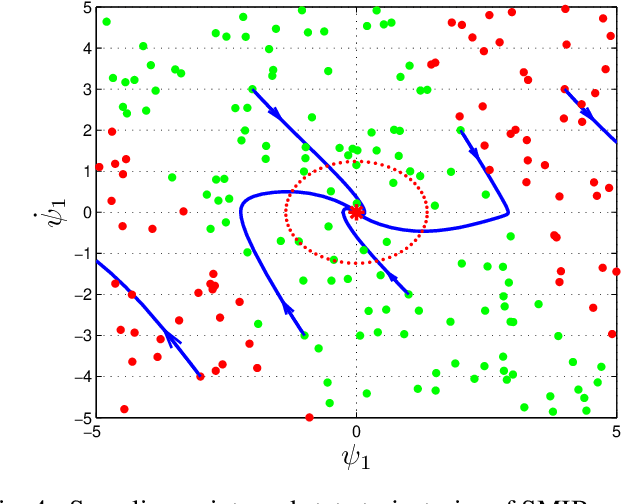
Abstract:This paper introduces a novel framework to construct the region of attraction (ROA) of a power system centered around a stable equilibrium by using stable state trajectories of system dynamics. Most existing works on estimating ROA rely on analytical Lyapunov functions, which are subject to two limitations: the analytic Lyapunov functions may not be always readily available, and the resulting ROA may be overly conservative. This work overcomes these two limitations by leveraging the converse Lyapunov theorem in control theory to eliminate the need of an analytic Lyapunov function and learning the unknown Lyapunov function with the Gaussian Process (GP) approach. In addition, a Gaussian Process Upper Confidence Bound (GP-UCB) based sampling algorithm is designed to reconcile the trade-off between the exploitation for enlarging the ROA and the exploration for reducing the uncertainty of sampling region. Within the constructed ROA, it is guaranteed in probability that the system state will converge to the stable equilibrium with a confidence level. Numerical simulations are also conducted to validate the assessment approach for the ROA of the single machine infinite bus system and the New England $39$-bus system. Numerical results demonstrate that our approach can significantly enlarge the estimated ROA compared to that of the analytic Lyapunov counterpart.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge