Optimization Proxies using Limited Labeled Data and Training Time -- A Semi-Supervised Bayesian Neural Network Approach

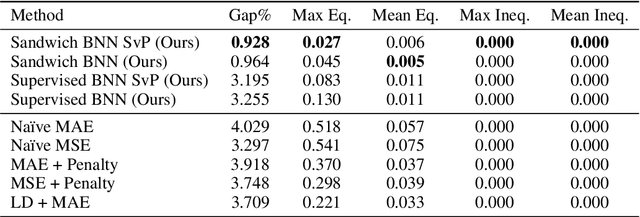
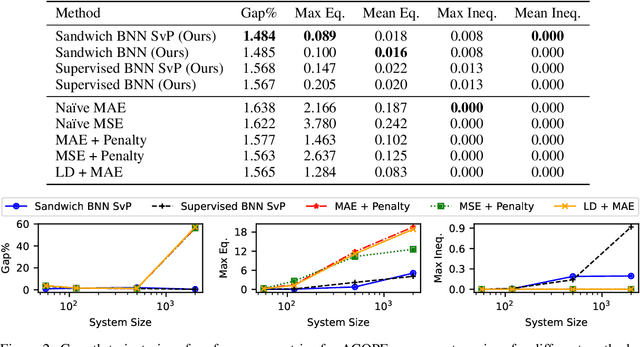
Constrained optimization problems arise in various engineering system operations such as inventory management and electric power grids. However, the requirement to repeatedly solve such optimization problems with uncertain parameters poses a significant computational challenge. This work introduces a learning scheme using Bayesian Neural Networks (BNNs) to solve constrained optimization problems under limited labeled data and restricted model training times. We propose a semi-supervised BNN for this practical but complex regime, wherein training commences in a sandwiched fashion, alternating between a supervised learning step (using labeled data) for minimizing cost, and an unsupervised learning step (using unlabeled data) for enforcing constraint feasibility. Both supervised and unsupervised steps use a Bayesian approach, where Stochastic Variational Inference is employed for approximate Bayesian inference. We show that the proposed semi-supervised learning method outperforms conventional BNN and deep neural network (DNN) architectures on important non-convex constrained optimization problems from energy network operations, achieving up to a tenfold reduction in expected maximum equality gap and halving the optimality and inequality (feasibility) gaps, without requiring any correction or projection step. By leveraging the BNN's ability to provide posterior samples at minimal computational cost, we demonstrate that a Selection via Posterior (SvP) scheme can further reduce equality gaps by more than 10%. We also provide tight and practically meaningful probabilistic confidence bounds that can be constructed using a low number of labeled testing data and readily adapted to other applications.