Distributed Difference of Convex Optimization

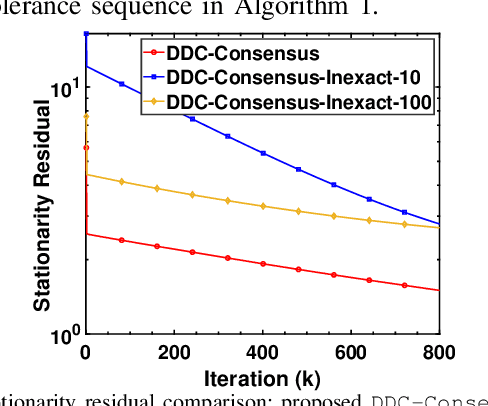
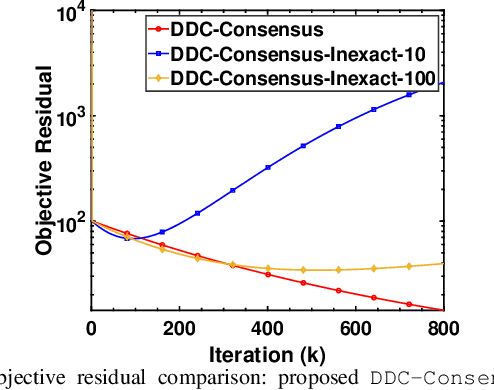
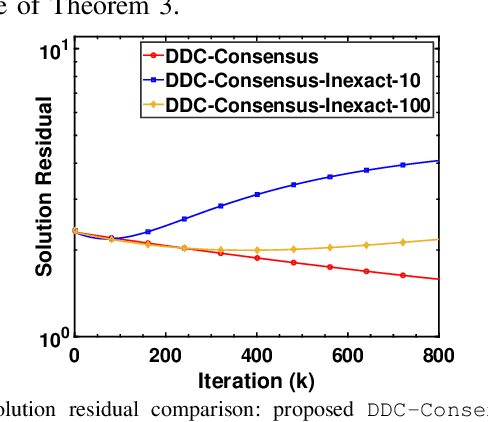
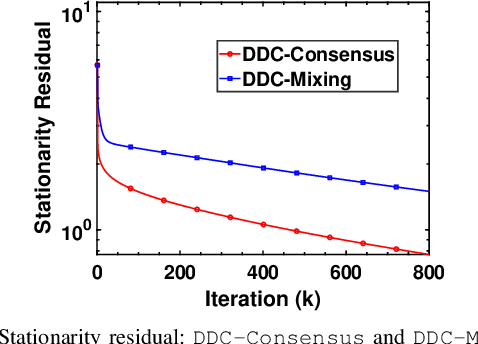
In this article, we focus on solving a class of distributed optimization problems involving $n$ agents with the local objective function at every agent $i$ given by the difference of two convex functions $f_i$ and $g_i$ (difference-of-convex (DC) form), where $f_i$ and $g_i$ are potentially nonsmooth. The agents communicate via a directed graph containing $n$ nodes. We create smooth approximations of the functions $f_i$ and $g_i$ and develop a distributed algorithm utilizing the gradients of the smooth surrogates and a finite-time approximate consensus protocol. We term this algorithm as DDC-Consensus. The developed DDC-Consensus algorithm allows for non-symmetric directed graph topologies and can be synthesized distributively. We establish that the DDC-Consensus algorithm converges to a stationary point of the nonconvex distributed optimization problem. The performance of the DDC-Consensus algorithm is evaluated via a simulation study to solve a nonconvex DC-regularized distributed least squares problem. The numerical results corroborate the efficacy of the proposed algorithm.

Causal Structure Recovery of Linear Dynamical Systems: An FFT based Approach

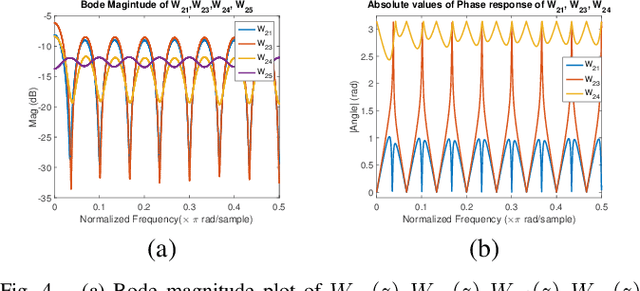
Learning causal effects from data is a fundamental and well-studied problem across science, especially when the cause-effect relationship is static in nature. However, causal effect is less explored when there are dynamical dependencies, i.e., when dependencies exist between entities across time. Identifying dynamic causal effects from time-series observations is computationally expensive when compared to the static scenario. We demonstrate that the computational complexity of recovering the causation structure for the vector auto-regressive (VAR) model is $O(Tn^3N^2)$, where $n$ is the number of nodes, $T$ is the number of samples, and $N$ is the largest time-lag in the dependency between entities. We report a method, with a reduced complexity of $O(Tn^3 \log N)$, to recover the causation structure to obtain frequency-domain (FD) representations of time-series. Since FFT accumulates all the time dependencies on every frequency, causal inference can be performed efficiently by considering the state variables as random variables at any given frequency. We additionally show that, for systems with interactions that are LTI, do-calculus machinery can be realized in the FD resulting in versions of the classical single-door (with cycles), front and backdoor criteria. We demonstrate, for a large class of problems, graph reconstruction using multivariate Wiener projections results in a significant computational advantage with $O(n)$ complexity over reconstruction algorithms such as the PC algorithm which has $O(n^q)$ complexity, where $q$ is the maximum neighborhood size. This advantage accrues due to some remarkable properties of the phase response of the frequency-dependent Wiener coefficients which is not present in any time-domain approach.

Information Theoretically Optimal Sample Complexity of Learning Dynamical Directed Acyclic Graphs

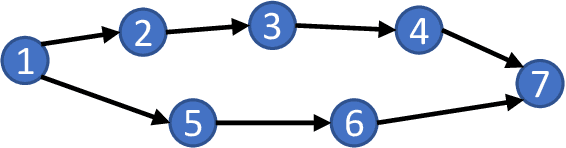
In this article, the optimal sample complexity of learning the underlying interaction/dependencies of a Linear Dynamical System (LDS) over a Directed Acyclic Graph (DAG) is studied. The sample complexity of learning a DAG's structure is well-studied for static systems, where the samples of nodal states are independent and identically distributed (i.i.d.). However, such a study is less explored for DAGs with dynamical systems, where the nodal states are temporally correlated. We call such a DAG underlying an LDS as \emph{dynamical} DAG (DDAG). In particular, we consider a DDAG where the nodal dynamics are driven by unobserved exogenous noise sources that are wide-sense stationary (WSS) in time but are mutually uncorrelated, and have the same {power spectral density (PSD)}. Inspired by the static settings, a metric and an algorithm based on the PSD matrix of the observed time series are proposed to reconstruct the DDAG. The equal noise PSD assumption can be relaxed such that identifiability conditions for DDAG reconstruction are not violated. For the LDS with WSS (sub) Gaussian exogenous noise sources, it is shown that the optimal sample complexity (or length of state trajectory) needed to learn the DDAG is $n=\Theta(q\log(p/q))$, where $p$ is the number of nodes and $q$ is the maximum number of parents per node. To prove the sample complexity upper bound, a concentration bound for the PSD estimation is derived, under two different sampling strategies. A matching min-max lower bound using generalized Fano's inequality also is provided, thus showing the order optimality of the proposed algorithm.

Physics Informed Topology Learning in Networks of Linear Dynamical Systems

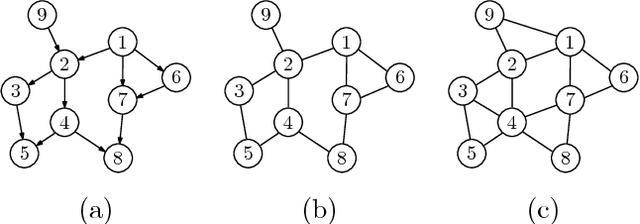
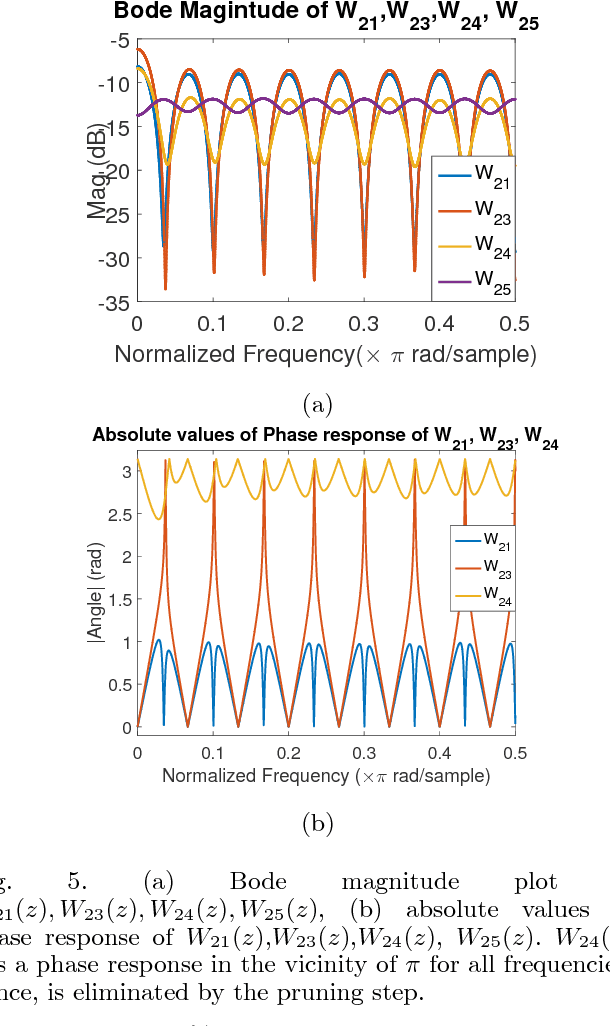
Learning influence pathways of a network of dynamically related processes from observations is of considerable importance in many disciplines. In this article, influence networks of agents which interact dynamically via linear dependencies are considered. An algorithm for the reconstruction of the topology of interaction based on multivariate Wiener filtering is analyzed. It is shown that for a vast and important class of interactions, that respect flow conservation, the topology of the interactions can be exactly recovered. The class of problems where reconstruction is guaranteed to be exact includes power distribution networks, dynamic thermal networks and consensus networks. The efficacy of the approach is illustrated through simulation and experiments on consensus networks, IEEE power distribution networks and thermal dynamics of buildings.

Learning the Exact Topology of Undirected Consensus Networks

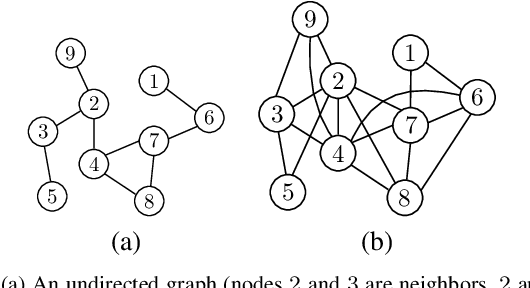
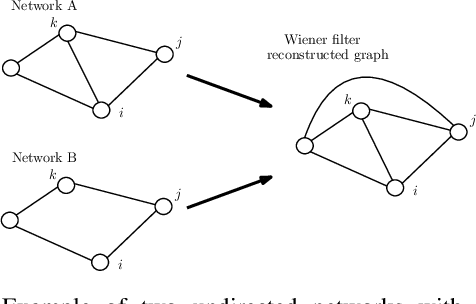
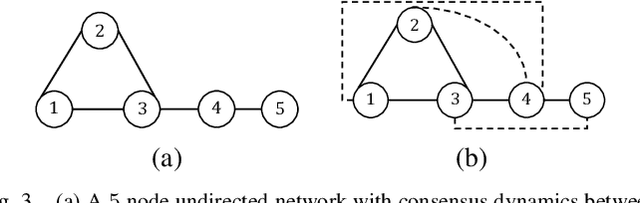
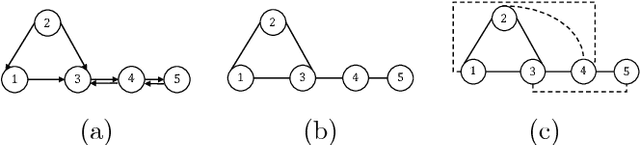
In this article, we present a method to learn the interaction topology of a network of agents undergoing linear consensus updates in a non invasive manner. Our approach is based on multivariate Wiener filtering, which is known to recover spurious edges apart from the true edges in the topology. The main contribution of this work is to show that in the case of undirected consensus networks, all spurious links obtained using Wiener filtering can be identified using frequency response of the Wiener filters. Thus, the exact interaction topology of the agents is unveiled. The method presented requires time series measurements of the state of the agents and does not require any knowledge of link weights. To the best of our knowledge this is the first approach that provably reconstructs the structure of undirected consensus networks with correlated noise. We illustrate the effectiveness of the method developed through numerical simulations as well as experiments on a five node network of Raspberry Pis.

Exact Topology Reconstruction of Radial Dynamical Systems with Applications to Distribution System of the Power Grid

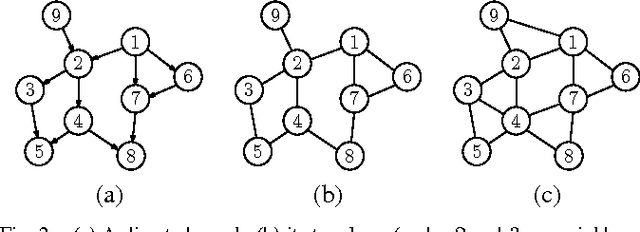
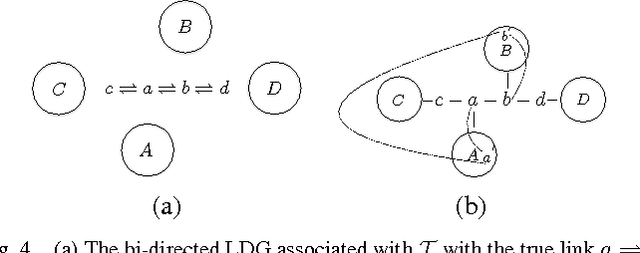
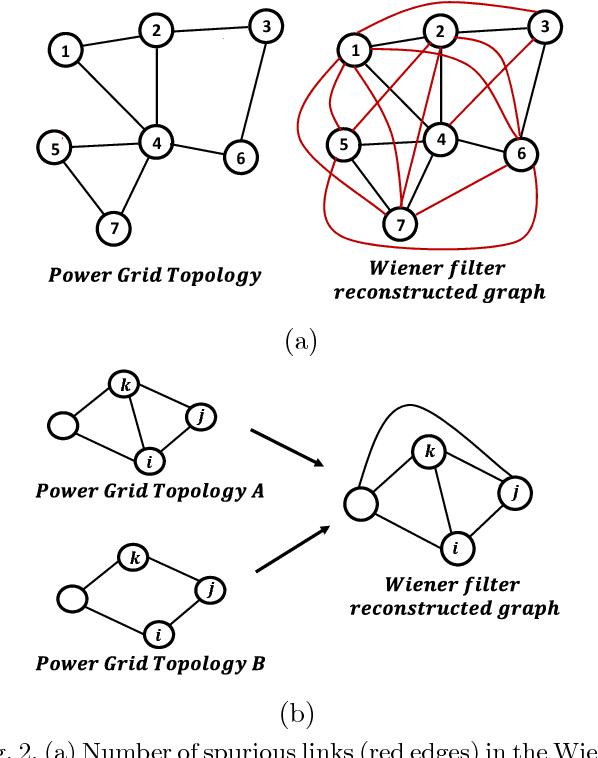
In this article we present a method to reconstruct the interconnectedness of dynamically related stochastic processes, where the interactions are bi-directional and the underlying topology is a tree. Our approach is based on multivariate Wiener filtering which recovers spurious edges apart from the true edges in the topology reconstruction. The main contribution of this work is to show that all spurious links obtained using Wiener filtering can be eliminated if the underlying topology is a tree based on which we present a three stage network reconstruction procedure for trees. We illustrate the effectiveness of the method developed by applying it on a typical distribution system of the electric grid.