Learning Networked Linear Dynamical Systems under Non-white Excitation from a Single Trajectory

We consider a networked linear dynamical system with $p$ agents/nodes. We study the problem of learning the underlying graph of interactions/dependencies from observations of the nodal trajectories over a time-interval $T$. We present a regularized non-casual consistent estimator for this problem and analyze its sample complexity over two regimes: (a) where the interval $T$ consists of $n$ i.i.d. observation windows of length $T/n$ (restart and record), and (b) where $T$ is one continuous observation window (consecutive). Using the theory of $M$-estimators, we show that the estimator recovers the underlying interactions, in either regime, in a time-interval that is logarithmic in the system size $p$. To the best of our knowledge, this is the first work to analyze the sample complexity of learning linear dynamical systems driven by unobserved not-white wide-sense stationary (WSS) inputs.

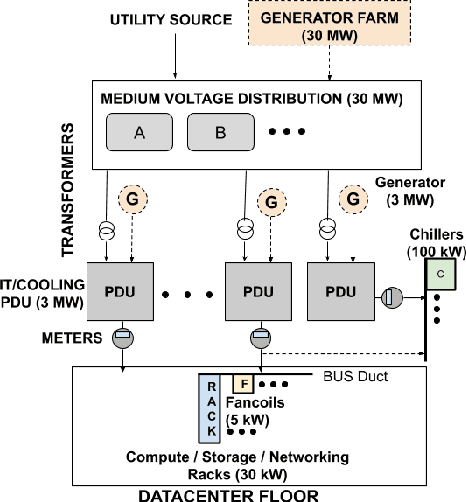
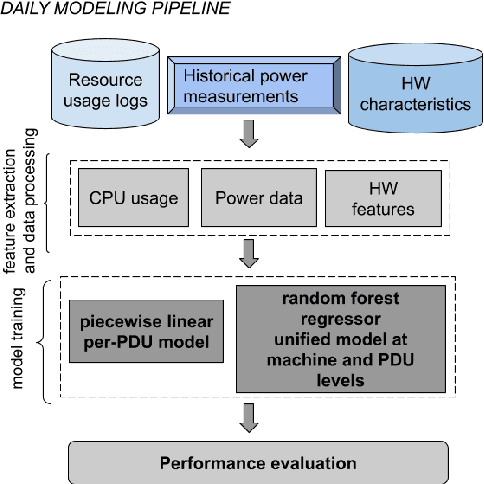
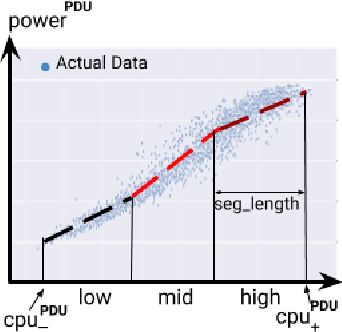
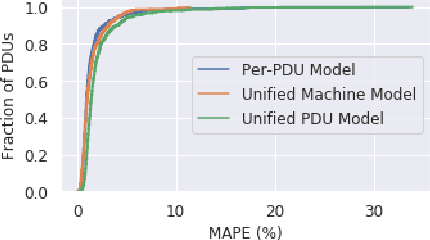
Power Modeling for Effective Datacenter Planning and Compute Management

Datacenter power demand has been continuously growing and is the key driver of its cost. An accurate mapping of compute resources (CPU, RAM, etc.) and hardware types (servers, accelerators, etc.) to power consumption has emerged as a critical requirement for major Web and cloud service providers. With the global growth in datacenter capacity and associated power consumption, such models are essential for important decisions around datacenter design and operation. In this paper, we discuss two classes of statistical power models designed and validated to be accurate, simple, interpretable and applicable to all hardware configurations and workloads across hyperscale datacenters of Google fleet. To the best of our knowledge, this is the largest scale power modeling study of this kind, in both the scope of diverse datacenter planning and real-time management use cases, as well as the variety of hardware configurations and workload types used for modeling and validation. We demonstrate that the proposed statistical modeling techniques, while simple and scalable, predict power with less than 5% Mean Absolute Percent Error (MAPE) for more than 95% diverse Power Distribution Units (more than 2000) using only 4 features. This performance matches the reported accuracy of the previous started-of-the-art methods, while using significantly less features and covering a wider range of use cases.

Estimating Linear Dynamical Networks of Cyclostationary Processes

Topology learning is an important problem in dynamical systems with implications to security and optimal control. The majority of prior work in consistent topology estimation relies on dynamical systems excited by temporally uncorrelated processes. In this article, we present a novel algorithm for guaranteed topology learning, in networks that are excited by temporally colored, cyclostationary processes. Furthermore, unlike prior work, the framework applies to linear dynamic system with complex valued dependencies. In the second part of the article, we analyze conditions for consistent topology learning for bidirected radial networks when a subset of the network is unobserved. Here, few agents are unobserved and the full topology along with unobserved nodes are recovered from observed agents data alone. Our theoretical contributions are validated on test networks.

Physics Informed Topology Learning in Networks of Linear Dynamical Systems

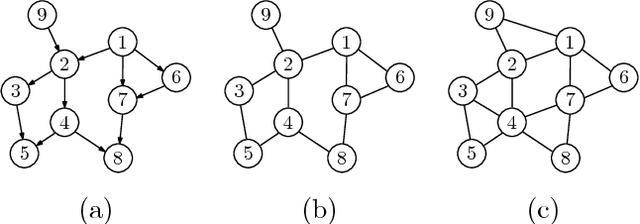
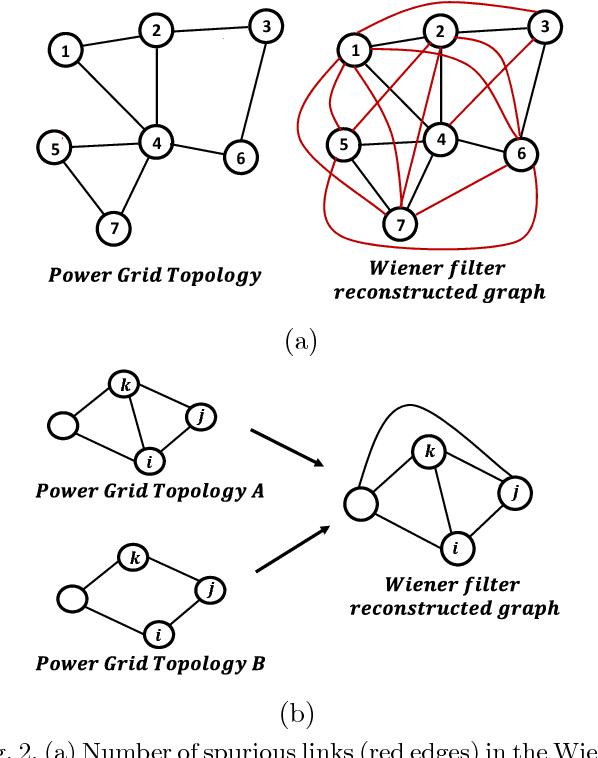
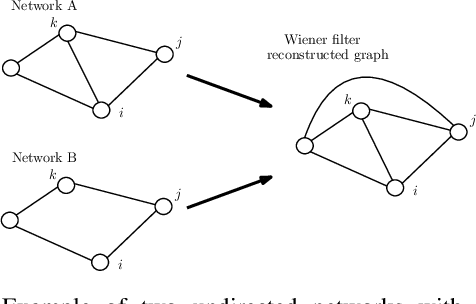
Learning influence pathways of a network of dynamically related processes from observations is of considerable importance in many disciplines. In this article, influence networks of agents which interact dynamically via linear dependencies are considered. An algorithm for the reconstruction of the topology of interaction based on multivariate Wiener filtering is analyzed. It is shown that for a vast and important class of interactions, that respect flow conservation, the topology of the interactions can be exactly recovered. The class of problems where reconstruction is guaranteed to be exact includes power distribution networks, dynamic thermal networks and consensus networks. The efficacy of the approach is illustrated through simulation and experiments on consensus networks, IEEE power distribution networks and thermal dynamics of buildings.

Learning the Exact Topology of Undirected Consensus Networks

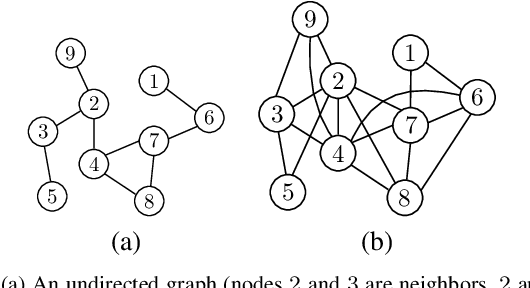
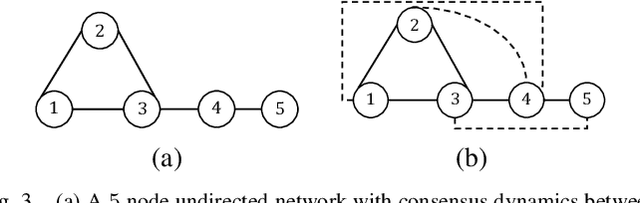
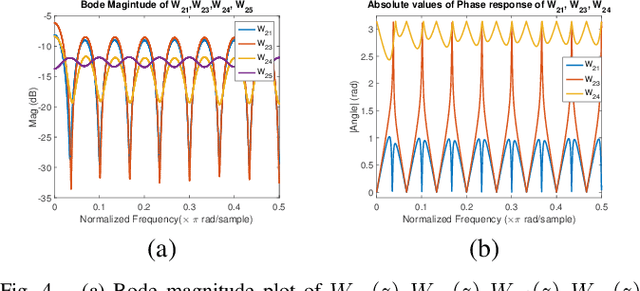
In this article, we present a method to learn the interaction topology of a network of agents undergoing linear consensus updates in a non invasive manner. Our approach is based on multivariate Wiener filtering, which is known to recover spurious edges apart from the true edges in the topology. The main contribution of this work is to show that in the case of undirected consensus networks, all spurious links obtained using Wiener filtering can be identified using frequency response of the Wiener filters. Thus, the exact interaction topology of the agents is unveiled. The method presented requires time series measurements of the state of the agents and does not require any knowledge of link weights. To the best of our knowledge this is the first approach that provably reconstructs the structure of undirected consensus networks with correlated noise. We illustrate the effectiveness of the method developed through numerical simulations as well as experiments on a five node network of Raspberry Pis.

Topology Estimation in Bulk Power Grids: Guarantees on Exact Recovery

The topology of a power grid affects its dynamic operation and settlement in the electricity market. Real-time topology identification can enable faster control action following an emergency scenario like failure of a line. This article discusses a graphical model framework for topology estimation in bulk power grids (both loopy transmission and radial distribution) using measurements of voltage collected from the grid nodes. The graphical model for the probability distribution of nodal voltages in linear power flow models is shown to include additional edges along with the operational edges in the true grid. Our proposed estimation algorithms first learn the graphical model and subsequently extract the operational edges using either thresholding or a neighborhood counting scheme. For grid topologies containing no three-node cycles (two buses do not share a common neighbor), we prove that an exact extraction of the operational topology is theoretically guaranteed. This includes a majority of distribution grids that have radial topologies. For grids that include cycles of length three, we provide sufficient conditions that ensure existence of algorithms for exact reconstruction. In particular, for grids with constant impedance per unit length and uniform injection covariances, this observation leads to conditions on geographical placement of the buses. The performance of algorithms is demonstrated in test case simulations.

Exact Topology Reconstruction of Radial Dynamical Systems with Applications to Distribution System of the Power Grid

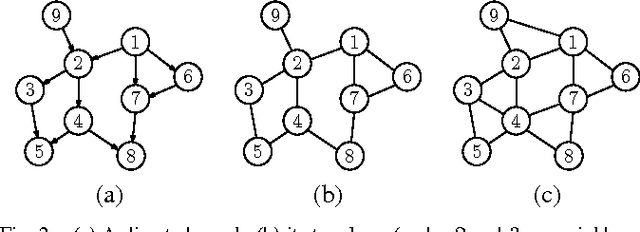
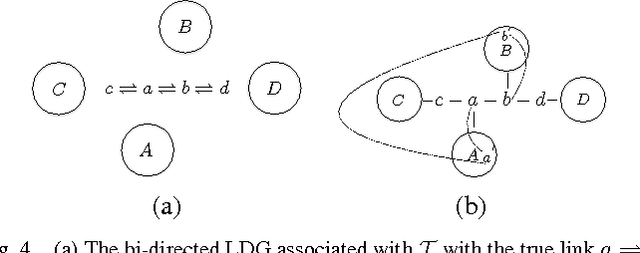
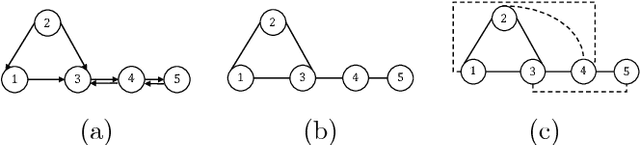
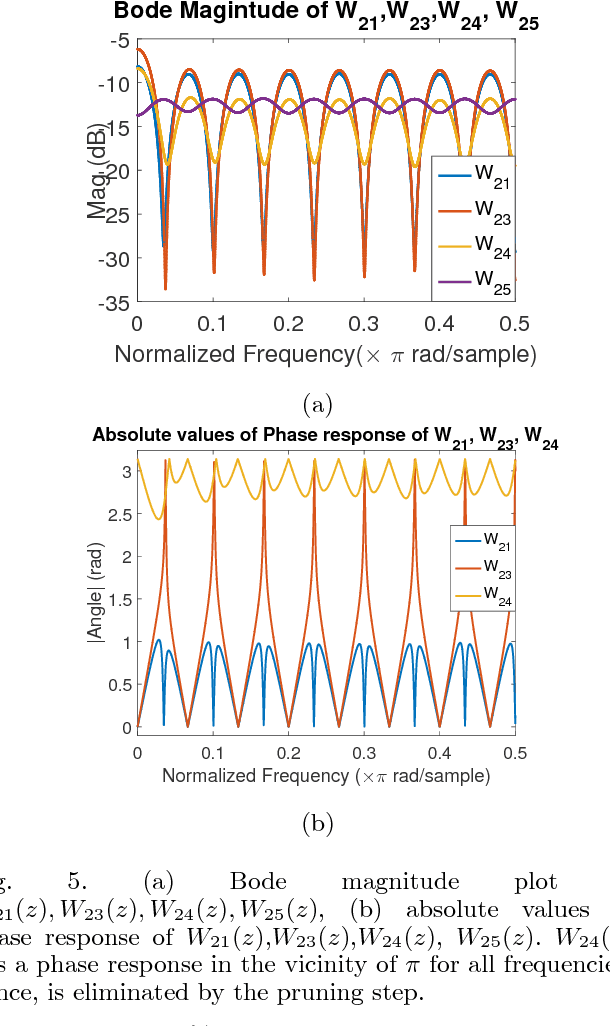
In this article we present a method to reconstruct the interconnectedness of dynamically related stochastic processes, where the interactions are bi-directional and the underlying topology is a tree. Our approach is based on multivariate Wiener filtering which recovers spurious edges apart from the true edges in the topology reconstruction. The main contribution of this work is to show that all spurious links obtained using Wiener filtering can be eliminated if the underlying topology is a tree based on which we present a three stage network reconstruction procedure for trees. We illustrate the effectiveness of the method developed by applying it on a typical distribution system of the electric grid.