An algorithm for reconstruction of triangle-free linear dynamic networks with verification of correctness

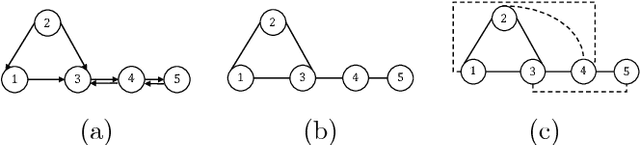
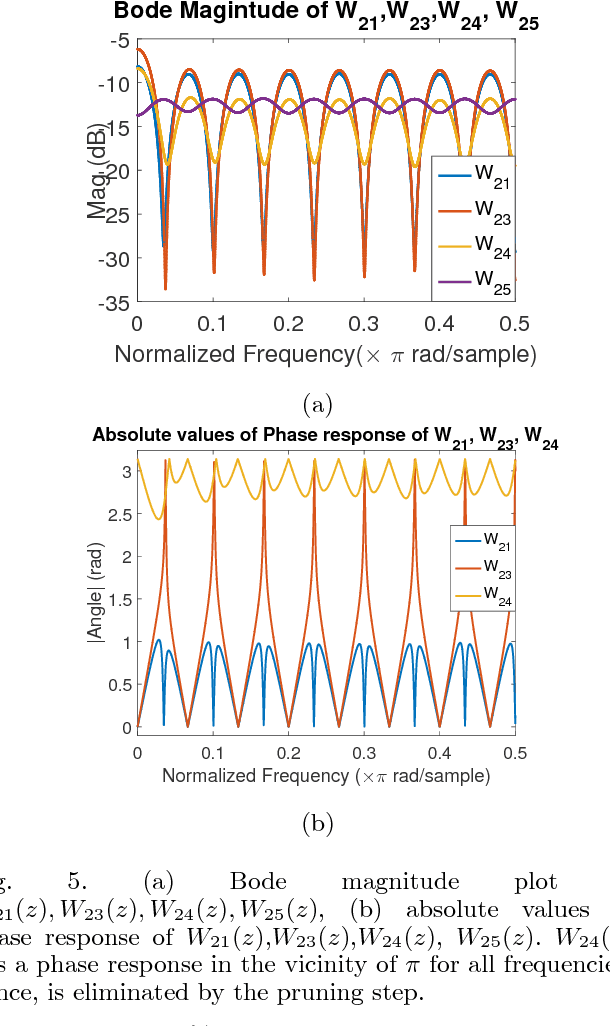
Reconstructing a network of dynamic systems from observational data is an active area of research. Many approaches guarantee a consistent reconstruction under the relatively strong assumption that the network dynamics is governed by strictly causal transfer functions. However, in many practical scenarios, strictly causal models are not adequate to describe the system and it is necessary to consider models with dynamics that include direct feedthrough terms. In presence of direct feedthroughs, guaranteeing a consistent reconstruction is a more challenging task. Indeed, under no additional assumptions on the network, we prove that, even in the limit of infinite data, any reconstruction method is susceptible to inferring edges that do not exist in the true network (false positives) or not detecting edges that are present in the network (false negative). However, for a class of triangle-free networks introduced in this article, some consistency guarantees can be provided. We present a method that either exactly recovers the topology of a triangle-free network certifying its correctness or outputs a graph that is sparser than the topology of the actual network, specifying that such a graph has no false positives, but there are false negatives.

Physics Informed Topology Learning in Networks of Linear Dynamical Systems

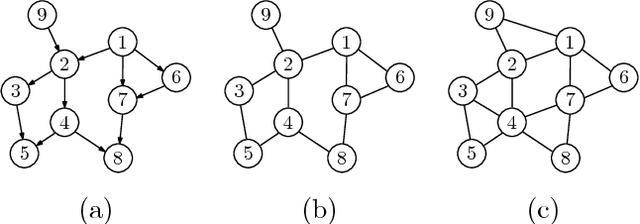
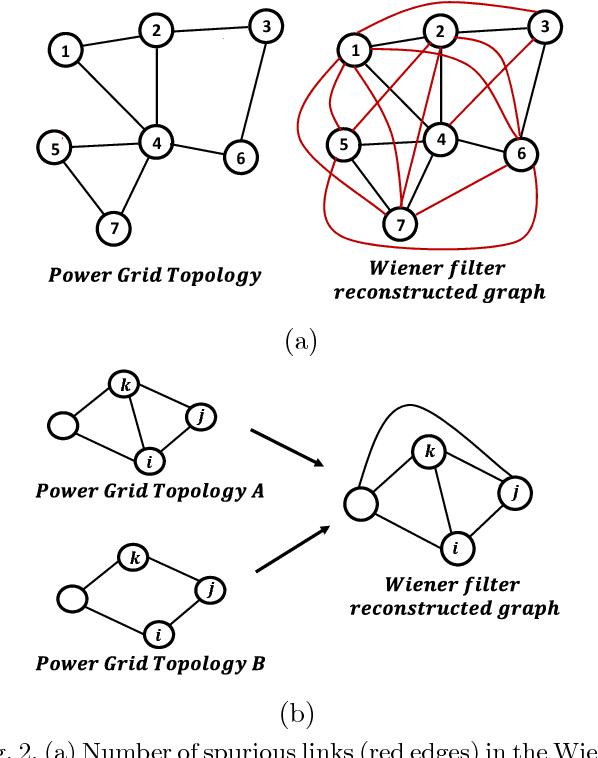
Learning influence pathways of a network of dynamically related processes from observations is of considerable importance in many disciplines. In this article, influence networks of agents which interact dynamically via linear dependencies are considered. An algorithm for the reconstruction of the topology of interaction based on multivariate Wiener filtering is analyzed. It is shown that for a vast and important class of interactions, that respect flow conservation, the topology of the interactions can be exactly recovered. The class of problems where reconstruction is guaranteed to be exact includes power distribution networks, dynamic thermal networks and consensus networks. The efficacy of the approach is illustrated through simulation and experiments on consensus networks, IEEE power distribution networks and thermal dynamics of buildings.

Learning the Exact Topology of Undirected Consensus Networks

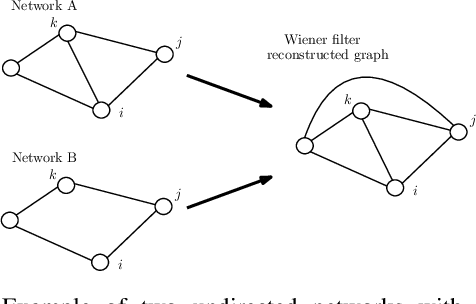
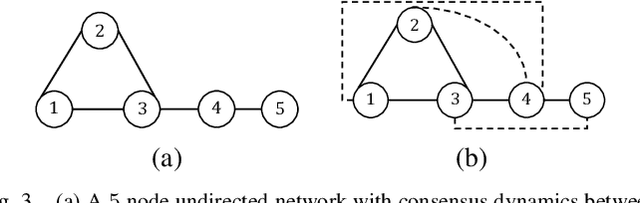
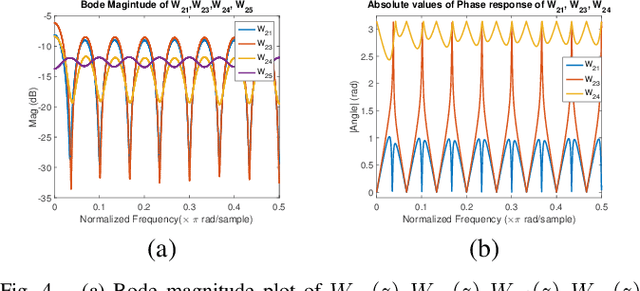
In this article, we present a method to learn the interaction topology of a network of agents undergoing linear consensus updates in a non invasive manner. Our approach is based on multivariate Wiener filtering, which is known to recover spurious edges apart from the true edges in the topology. The main contribution of this work is to show that in the case of undirected consensus networks, all spurious links obtained using Wiener filtering can be identified using frequency response of the Wiener filters. Thus, the exact interaction topology of the agents is unveiled. The method presented requires time series measurements of the state of the agents and does not require any knowledge of link weights. To the best of our knowledge this is the first approach that provably reconstructs the structure of undirected consensus networks with correlated noise. We illustrate the effectiveness of the method developed through numerical simulations as well as experiments on a five node network of Raspberry Pis.

Exact Topology Reconstruction of Radial Dynamical Systems with Applications to Distribution System of the Power Grid

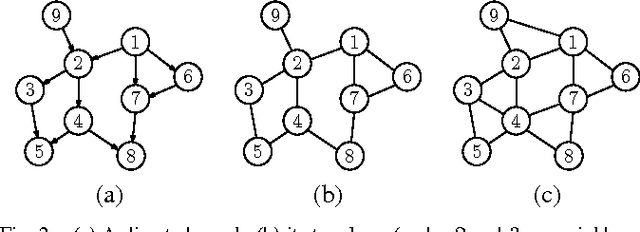
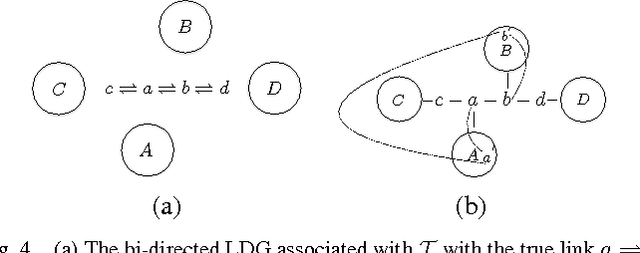
In this article we present a method to reconstruct the interconnectedness of dynamically related stochastic processes, where the interactions are bi-directional and the underlying topology is a tree. Our approach is based on multivariate Wiener filtering which recovers spurious edges apart from the true edges in the topology reconstruction. The main contribution of this work is to show that all spurious links obtained using Wiener filtering can be eliminated if the underlying topology is a tree based on which we present a three stage network reconstruction procedure for trees. We illustrate the effectiveness of the method developed by applying it on a typical distribution system of the electric grid.