Learning Networked Linear Dynamical Systems under Non-white Excitation from a Single Trajectory

We consider a networked linear dynamical system with $p$ agents/nodes. We study the problem of learning the underlying graph of interactions/dependencies from observations of the nodal trajectories over a time-interval $T$. We present a regularized non-casual consistent estimator for this problem and analyze its sample complexity over two regimes: (a) where the interval $T$ consists of $n$ i.i.d. observation windows of length $T/n$ (restart and record), and (b) where $T$ is one continuous observation window (consecutive). Using the theory of $M$-estimators, we show that the estimator recovers the underlying interactions, in either regime, in a time-interval that is logarithmic in the system size $p$. To the best of our knowledge, this is the first work to analyze the sample complexity of learning linear dynamical systems driven by unobserved not-white wide-sense stationary (WSS) inputs.

Estimating Linear Dynamical Networks of Cyclostationary Processes

Topology learning is an important problem in dynamical systems with implications to security and optimal control. The majority of prior work in consistent topology estimation relies on dynamical systems excited by temporally uncorrelated processes. In this article, we present a novel algorithm for guaranteed topology learning, in networks that are excited by temporally colored, cyclostationary processes. Furthermore, unlike prior work, the framework applies to linear dynamic system with complex valued dependencies. In the second part of the article, we analyze conditions for consistent topology learning for bidirected radial networks when a subset of the network is unobserved. Here, few agents are unobserved and the full topology along with unobserved nodes are recovered from observed agents data alone. Our theoretical contributions are validated on test networks.

Tractable learning in under-excited power grids

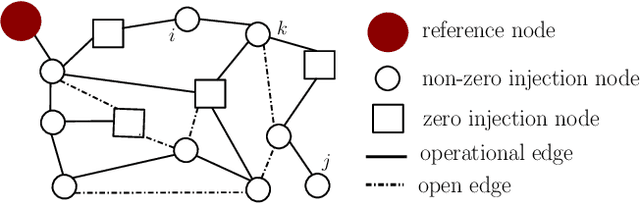
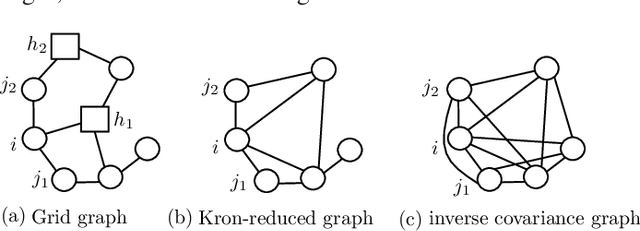
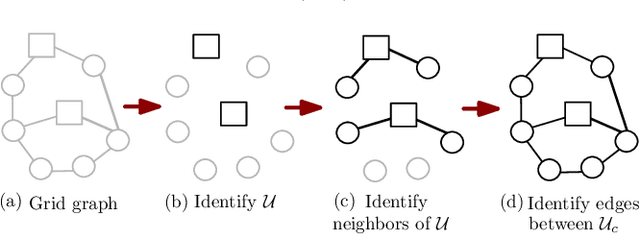
Estimating the structure of physical flow networks such as power grids is critical to secure delivery of energy. This paper discusses statistical structure estimation in power grids in the "under-excited" regime, where a subset of internal nodes do not have external injection. Prior estimation algorithms based on nodal potentials or voltages fail in the under-excited regime. We propose a novel topology learning algorithm for learning underexcited general (non-radial) networks based on physics-informed conservation laws. We prove the asymptotic correctness of our algorithm for grids with non-adjacent under-excited internal nodes. More importantly, we theoretically analyze our algorithm's efficacy under noisy measurements, and determine bounds on maximum noise under which asymptotically correct recovery is guaranteed. Our approach is validated through simulations with non-linear voltage samples generated on test grids with real injection data

Physics Informed Topology Learning in Networks of Linear Dynamical Systems

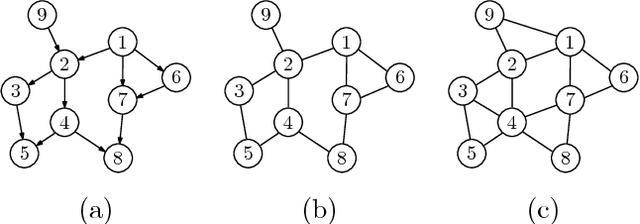
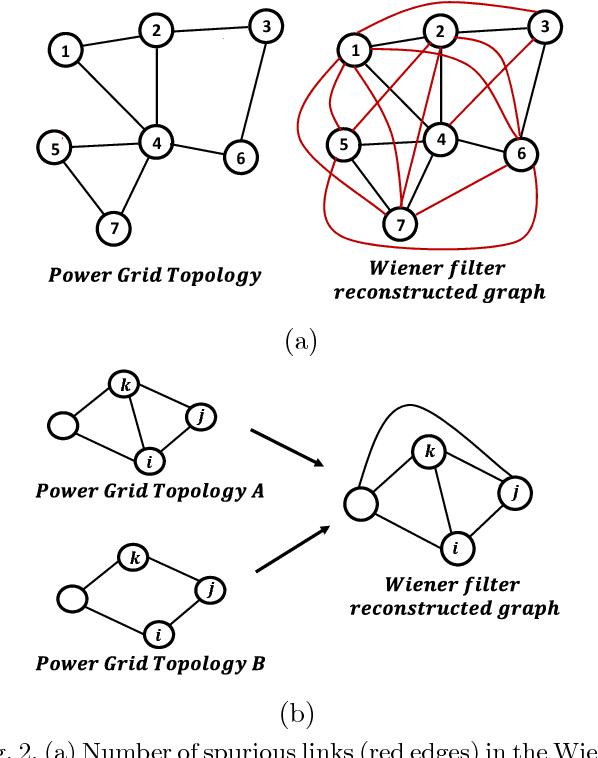
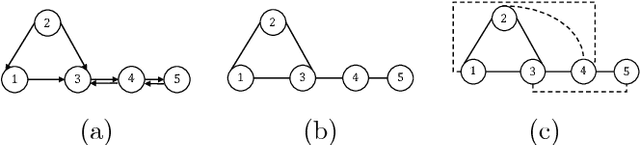
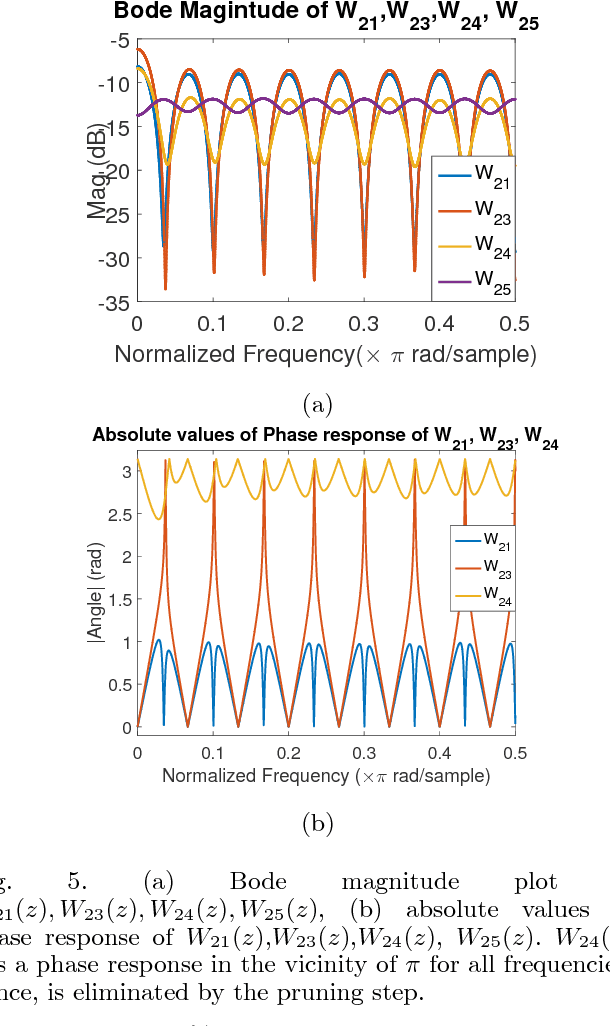
Learning influence pathways of a network of dynamically related processes from observations is of considerable importance in many disciplines. In this article, influence networks of agents which interact dynamically via linear dependencies are considered. An algorithm for the reconstruction of the topology of interaction based on multivariate Wiener filtering is analyzed. It is shown that for a vast and important class of interactions, that respect flow conservation, the topology of the interactions can be exactly recovered. The class of problems where reconstruction is guaranteed to be exact includes power distribution networks, dynamic thermal networks and consensus networks. The efficacy of the approach is illustrated through simulation and experiments on consensus networks, IEEE power distribution networks and thermal dynamics of buildings.