AdUE: Improving uncertainty estimation head for LoRA adapters in LLMs

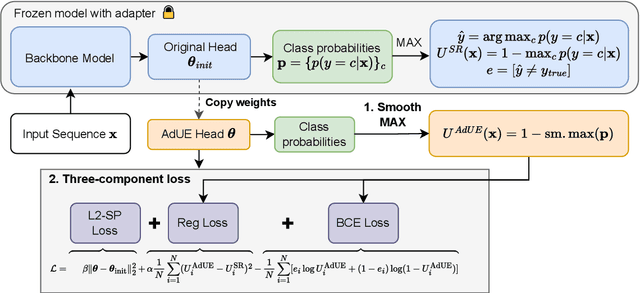
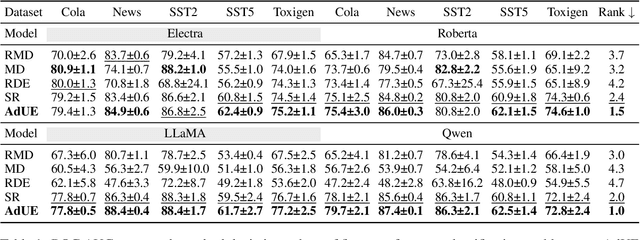
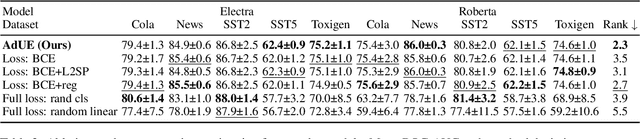
Uncertainty estimation remains a critical challenge in adapting pre-trained language models to classification tasks, particularly under parameter-efficient fine-tuning approaches such as adapters. We introduce AdUE1, an efficient post-hoc uncertainty estimation (UE) method, to enhance softmax-based estimates. Our approach (1) uses a differentiable approximation of the maximum function and (2) applies additional regularization through L2-SP, anchoring the fine-tuned head weights and regularizing the model. Evaluations on five NLP classification datasets across four language models (RoBERTa, ELECTRA, LLaMA-2, Qwen) demonstrate that our method consistently outperforms established baselines such as Mahalanobis distance and softmax response. Our approach is lightweight (no base-model changes) and produces better-calibrated confidence.

Supervised Learning based Method for Condition Monitoring of Overhead Line Insulators using Leakage Current Measurement

As a new practical and economical solution to the aging problem of overhead line (OHL) assets, the technical policies of most power grid companies in the world experienced a gradual transition from scheduled preventive maintenance to a risk-based approach in asset management. Even though the accumulation of contamination is predictable within a certain degree, there are currently no effective ways to identify the risk of the insulator flashover in order to plan its replacement. This paper presents a novel machine learning (ML) based method for estimating the flashover probability of the cup-and-pin glass insulator string. The proposed method is based on the Extreme Gradient Boosting (XGBoost) supervised ML model, in which the leakage current (LC) features and applied voltage are used as the inputs. The established model can estimate the critical flashover voltage (U50%) for various designs of OHL insulators with different voltage levels. The proposed method is also able to accurately determine the condition of the insulator strings and instruct asset management engineers to take appropriate actions.

Data-Driven Stochastic AC-OPF using Gaussian Processes

The thesis focuses on developing a data-driven algorithm, based on machine learning, to solve the stochastic alternating current (AC) chance-constrained (CC) Optimal Power Flow (OPF) problem. Although the AC CC-OPF problem has been successful in academic circles, it is highly nonlinear and computationally demanding, which limits its practical impact. The proposed approach aims to address this limitation and demonstrate its empirical efficiency through applications to multiple IEEE test cases. To solve the non-convex and computationally challenging CC AC-OPF problem, the proposed approach relies on a machine learning Gaussian process regression (GPR) model. The full Gaussian process (GP) approach is capable of learning a simple yet non-convex data-driven approximation to the AC power flow equations that can incorporate uncertain inputs. The proposed approach uses various approximations for GP-uncertainty propagation. The full GP CC-OPF approach exhibits highly competitive and promising results, outperforming the state-of-the-art sample-based chance constraint approaches. To further improve the robustness and complexity/accuracy trade-off of the full GP CC-OPF, a fast data-driven setup is proposed. This setup relies on the sparse and hybrid Gaussian processes (GP) framework to model the power flow equations with input uncertainty.

Supporting Future Electrical Utilities: Using Deep Learning Methods in EMS and DMS Algorithms

Electrical power systems are increasing in size, complexity, as well as dynamics due to the growing integration of renewable energy resources, which have sporadic power generation. This necessitates the development of near real-time power system algorithms, demanding lower computational complexity regarding the power system size. Considering the growing trend in the collection of historical measurement data and recent advances in the rapidly developing deep learning field, the main goal of this paper is to provide a review of recent deep learning-based power system monitoring and optimization algorithms. Electrical utilities can benefit from this review by re-implementing or enhancing the algorithms traditionally used in energy management systems (EMS) and distribution management systems (DMS).

GP CC-OPF: Gaussian Process based optimization tool for Chance-Constrained Optimal Power Flow

The Gaussian Process (GP) based Chance-Constrained Optimal Power Flow (CC-OPF) is an open-source Python code developed for solving economic dispatch (ED) problem in modern power grids. In recent years, integrating a significant amount of renewables into a power grid causes high fluctuations and thus brings a lot of uncertainty to power grid operations. This fact makes the conventional model-based CC-OPF problem non-convex and computationally complex to solve. The developed tool presents a novel data-driven approach based on the GP regression model for solving the CC-OPF problem with a trade-off between complexity and accuracy. The proposed approach and developed software can help system operators to effectively perform ED optimization in the presence of large uncertainties in the power grid.

Power System Anomaly Detection and Classification Utilizing WLS-EKF State Estimation and Machine Learning

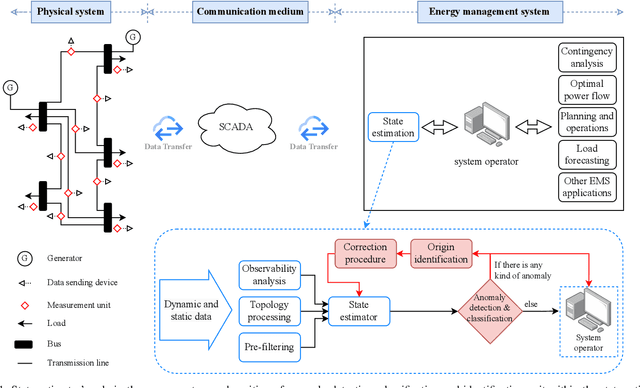
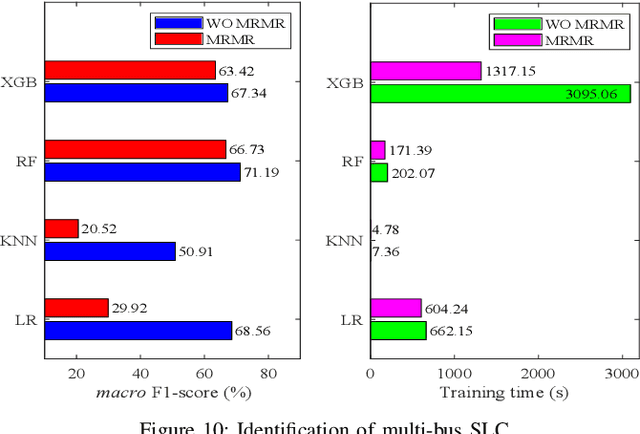
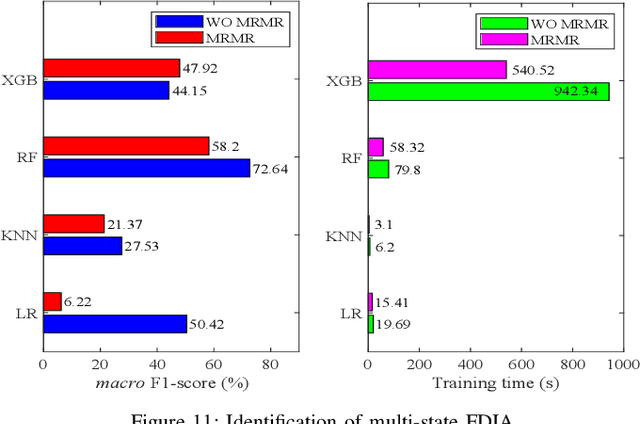
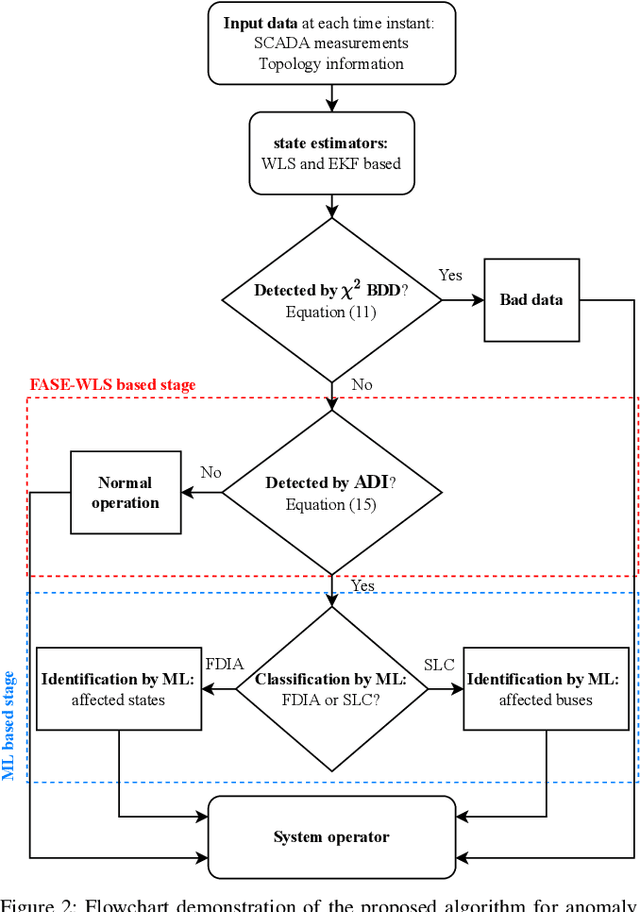
Power system state estimation is being faced with different types of anomalies. These might include bad data caused by gross measurement errors or communication system failures. Sudden changes in load or generation can be considered as anomaly depending on the implemented state estimation method. Additionally, considering power grid as a cyber physical system, state estimation becomes vulnerable to false data injection attacks. The existing methods for anomaly classification cannot accurately classify (discriminate between) the above mentioned three types of anomalies, especially when it comes to discrimination between sudden load changes and false data injection attacks. This paper presents a new algorithm for detecting anomaly presence, classifying the anomaly type and identifying the origin of the anomaly, i.e., measurements that contain gross errors in case of bad data, or buses associated with loads experiencing a sudden change, or state variables targeted by false data injection attack. The algorithm combines analytical and machine learning (ML) approaches. The first stage exploits an analytical approach to detect anomaly presence by combining $\chi^2$-test and anomaly detection index. The second stage utilizes ML for classification of anomaly type and identification of its origin, with particular reference to discrimination between sudden load changes and false data injection attacks. The proposed ML based method is trained to be independent of the network configuration which eliminates retraining of the algorithm after network topology changes. The results obtained by implementing the proposed algorithm on IEEE 14 bus test system demonstrate the accuracy and effectiveness of the proposed algorithm.

Data-Driven Chance Constrained AC-OPF using Hybrid Sparse Gaussian Processes

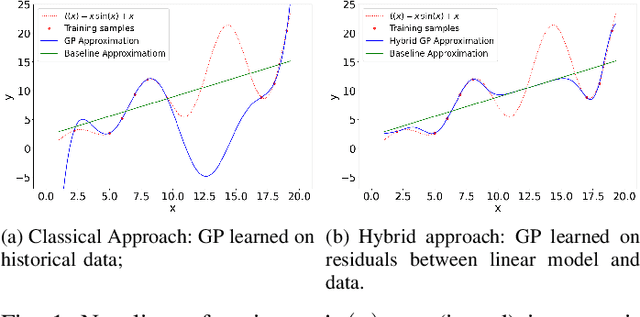
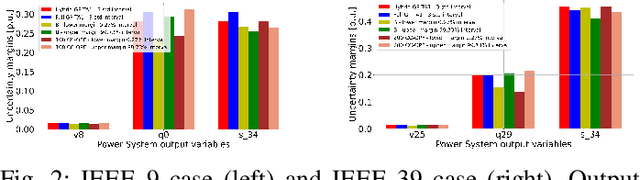
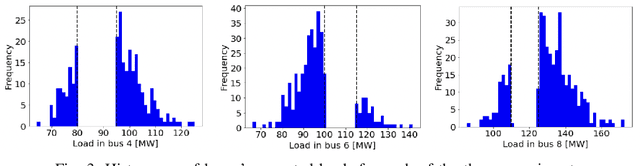
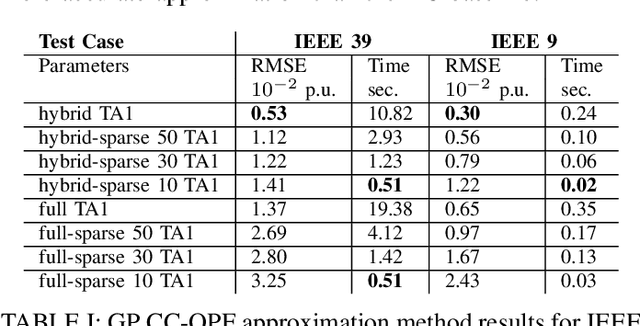
The alternating current (AC) chance-constrained optimal power flow (CC-OPF) problem addresses the economic efficiency of electricity generation and delivery under generation uncertainty. The latter is intrinsic to modern power grids because of the high amount of renewables. Despite its academic success, the AC CC-OPF problem is highly nonlinear and computationally demanding, which limits its practical impact. For improving the AC-OPF problem complexity/accuracy trade-off, the paper proposes a fast data-driven setup that uses the sparse and hybrid Gaussian processes (GP) framework to model the power flow equations with input uncertainty. We advocate the efficiency of the proposed approach by a numerical study over multiple IEEE test cases showing up to two times faster and more accurate solutions compared to the state-of-the-art methods.