CMIP X-MOS: Improving Climate Models with Extreme Model Output Statistics

Climate models are essential for assessing the impact of greenhouse gas emissions on our changing climate and the resulting increase in the frequency and severity of natural disasters. Despite the widespread acceptance of climate models produced by the Coupled Model Intercomparison Project (CMIP), they still face challenges in accurately predicting climate extremes, which pose most significant threats to both people and the environment. To address this limitation and improve predictions of natural disaster risks, we introduce Extreme Model Output Statistics (X-MOS). This approach utilizes deep regression techniques to precisely map CMIP model outputs to real measurements obtained from weather stations, which results in a more accurate analysis of the XXI climate extremes. In contrast to previous research, our study places a strong emphasis on enhancing the estimation of the tails of future climate parameter distributions. The latter supports decision-makers, enabling them to better assess climate-related risks across the globe.

GP CC-OPF: Gaussian Process based optimization tool for Chance-Constrained Optimal Power Flow

The Gaussian Process (GP) based Chance-Constrained Optimal Power Flow (CC-OPF) is an open-source Python code developed for solving economic dispatch (ED) problem in modern power grids. In recent years, integrating a significant amount of renewables into a power grid causes high fluctuations and thus brings a lot of uncertainty to power grid operations. This fact makes the conventional model-based CC-OPF problem non-convex and computationally complex to solve. The developed tool presents a novel data-driven approach based on the GP regression model for solving the CC-OPF problem with a trade-off between complexity and accuracy. The proposed approach and developed software can help system operators to effectively perform ED optimization in the presence of large uncertainties in the power grid.

Data-Driven Chance Constrained AC-OPF using Hybrid Sparse Gaussian Processes

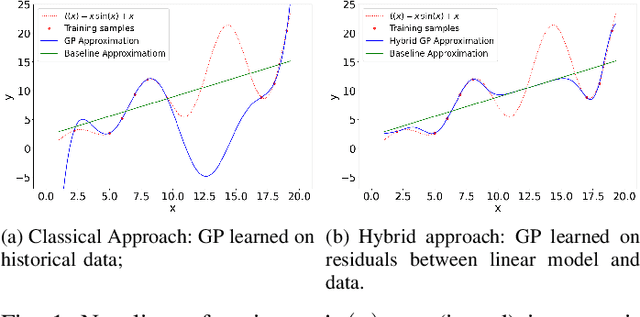
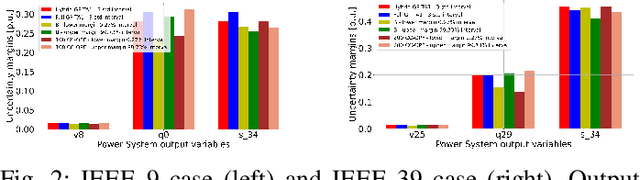
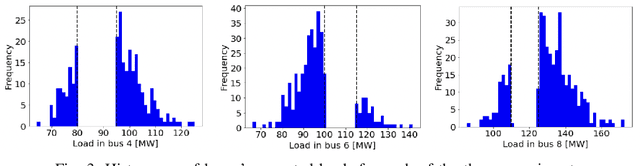
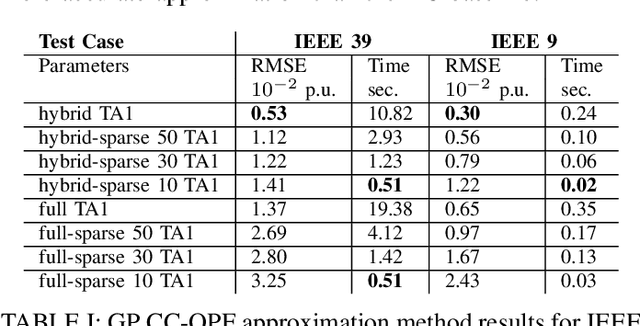
The alternating current (AC) chance-constrained optimal power flow (CC-OPF) problem addresses the economic efficiency of electricity generation and delivery under generation uncertainty. The latter is intrinsic to modern power grids because of the high amount of renewables. Despite its academic success, the AC CC-OPF problem is highly nonlinear and computationally demanding, which limits its practical impact. For improving the AC-OPF problem complexity/accuracy trade-off, the paper proposes a fast data-driven setup that uses the sparse and hybrid Gaussian processes (GP) framework to model the power flow equations with input uncertainty. We advocate the efficiency of the proposed approach by a numerical study over multiple IEEE test cases showing up to two times faster and more accurate solutions compared to the state-of-the-art methods.

Data-Driven Stochastic AC-OPF using Gaussian Processes

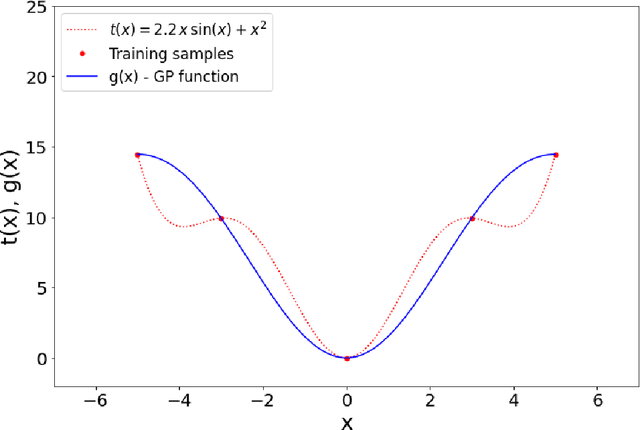
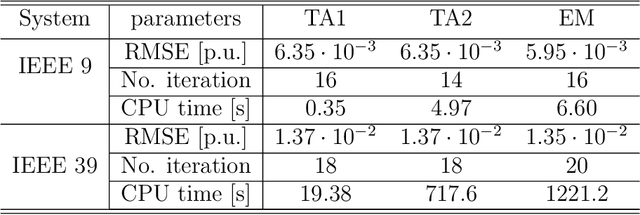
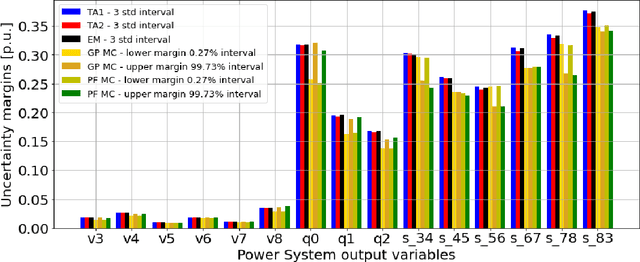
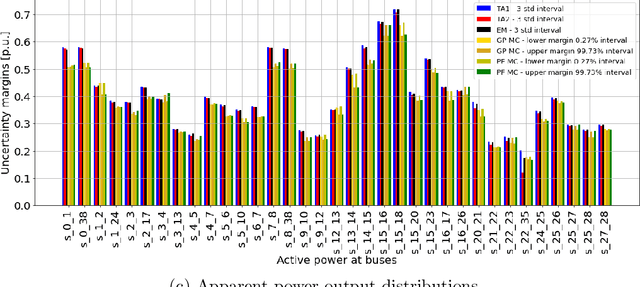
In recent years, electricity generation has been responsible for more than a quarter of the greenhouse gas emissions in the US. Integrating a significant amount of renewables into a power grid is probably the most accessible way to reduce carbon emissions from power grids and slow down climate change. Unfortunately, the most accessible renewable power sources, such as wind and solar, are highly fluctuating and thus bring a lot of uncertainty to power grid operations and challenge existing optimization and control policies. The chance-constrained alternating current (AC) optimal power flow (OPF) framework finds the minimum cost generation dispatch maintaining the power grid operations within security limits with a prescribed probability. Unfortunately, the AC-OPF problem's chance-constrained extension is non-convex, computationally challenging, and requires knowledge of system parameters and additional assumptions on the behavior of renewable distribution. Known linear and convex approximations to the above problems, though tractable, are too conservative for operational practice and do not consider uncertainty in system parameters. This paper presents an alternative data-driven approach based on Gaussian process (GP) regression to close this gap. The GP approach learns a simple yet non-convex data-driven approximation to the AC power flow equations that can incorporate uncertainty inputs. The latter is then used to determine the solution of CC-OPF efficiently, by accounting for both input and parameter uncertainty. The practical efficiency of the proposed approach using different approximations for GP-uncertainty propagation is illustrated over numerous IEEE test cases.