Supervised Learning based Method for Condition Monitoring of Overhead Line Insulators using Leakage Current Measurement

As a new practical and economical solution to the aging problem of overhead line (OHL) assets, the technical policies of most power grid companies in the world experienced a gradual transition from scheduled preventive maintenance to a risk-based approach in asset management. Even though the accumulation of contamination is predictable within a certain degree, there are currently no effective ways to identify the risk of the insulator flashover in order to plan its replacement. This paper presents a novel machine learning (ML) based method for estimating the flashover probability of the cup-and-pin glass insulator string. The proposed method is based on the Extreme Gradient Boosting (XGBoost) supervised ML model, in which the leakage current (LC) features and applied voltage are used as the inputs. The established model can estimate the critical flashover voltage (U50%) for various designs of OHL insulators with different voltage levels. The proposed method is also able to accurately determine the condition of the insulator strings and instruct asset management engineers to take appropriate actions.

GP CC-OPF: Gaussian Process based optimization tool for Chance-Constrained Optimal Power Flow

The Gaussian Process (GP) based Chance-Constrained Optimal Power Flow (CC-OPF) is an open-source Python code developed for solving economic dispatch (ED) problem in modern power grids. In recent years, integrating a significant amount of renewables into a power grid causes high fluctuations and thus brings a lot of uncertainty to power grid operations. This fact makes the conventional model-based CC-OPF problem non-convex and computationally complex to solve. The developed tool presents a novel data-driven approach based on the GP regression model for solving the CC-OPF problem with a trade-off between complexity and accuracy. The proposed approach and developed software can help system operators to effectively perform ED optimization in the presence of large uncertainties in the power grid.

Data-Driven Chance Constrained AC-OPF using Hybrid Sparse Gaussian Processes

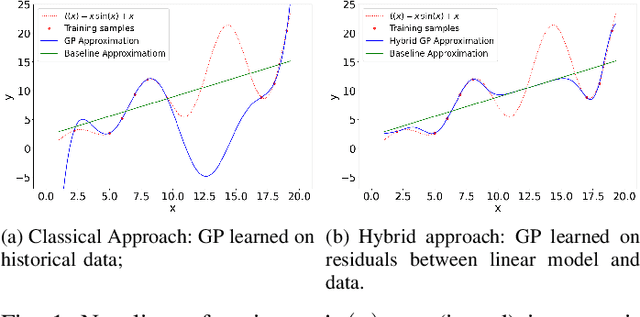
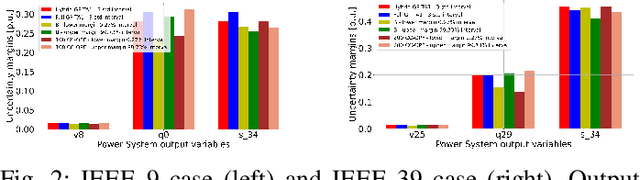
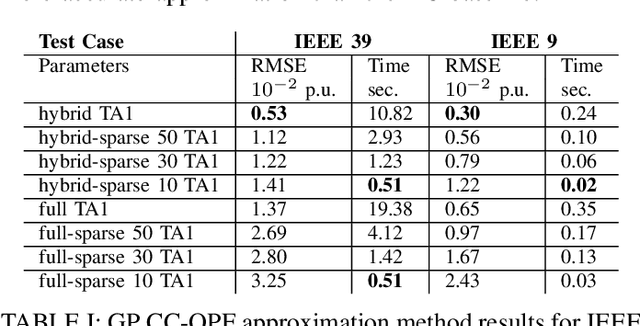
The alternating current (AC) chance-constrained optimal power flow (CC-OPF) problem addresses the economic efficiency of electricity generation and delivery under generation uncertainty. The latter is intrinsic to modern power grids because of the high amount of renewables. Despite its academic success, the AC CC-OPF problem is highly nonlinear and computationally demanding, which limits its practical impact. For improving the AC-OPF problem complexity/accuracy trade-off, the paper proposes a fast data-driven setup that uses the sparse and hybrid Gaussian processes (GP) framework to model the power flow equations with input uncertainty. We advocate the efficiency of the proposed approach by a numerical study over multiple IEEE test cases showing up to two times faster and more accurate solutions compared to the state-of-the-art methods.

Data-Driven Stochastic AC-OPF using Gaussian Processes

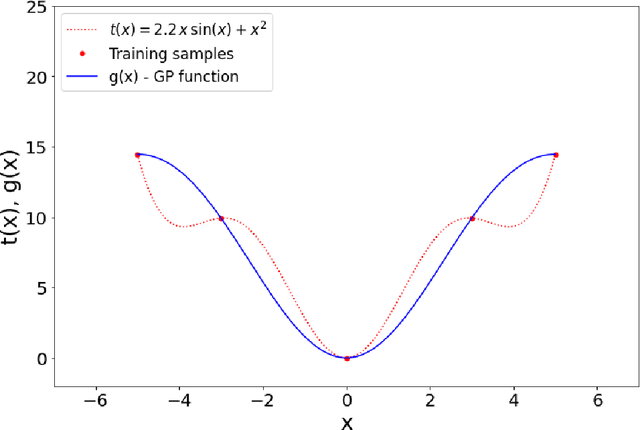
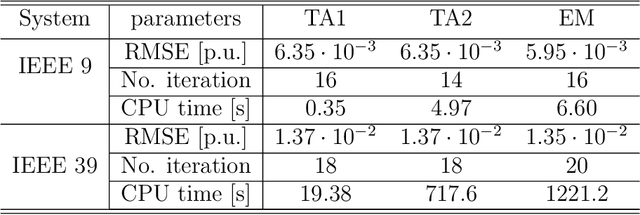
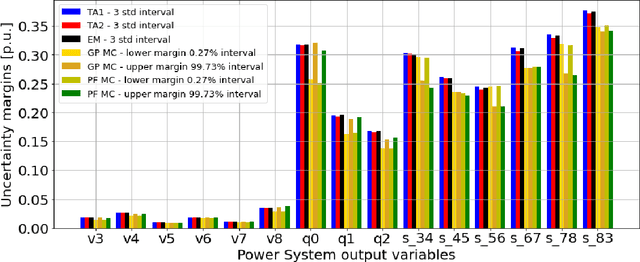
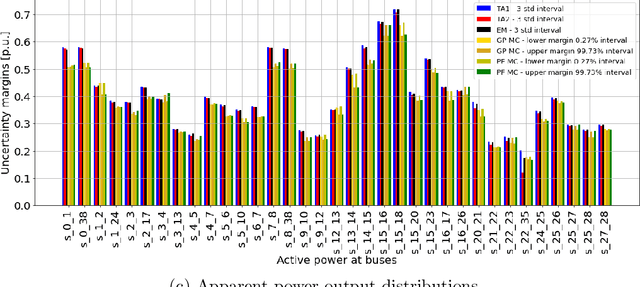
In recent years, electricity generation has been responsible for more than a quarter of the greenhouse gas emissions in the US. Integrating a significant amount of renewables into a power grid is probably the most accessible way to reduce carbon emissions from power grids and slow down climate change. Unfortunately, the most accessible renewable power sources, such as wind and solar, are highly fluctuating and thus bring a lot of uncertainty to power grid operations and challenge existing optimization and control policies. The chance-constrained alternating current (AC) optimal power flow (OPF) framework finds the minimum cost generation dispatch maintaining the power grid operations within security limits with a prescribed probability. Unfortunately, the AC-OPF problem's chance-constrained extension is non-convex, computationally challenging, and requires knowledge of system parameters and additional assumptions on the behavior of renewable distribution. Known linear and convex approximations to the above problems, though tractable, are too conservative for operational practice and do not consider uncertainty in system parameters. This paper presents an alternative data-driven approach based on Gaussian process (GP) regression to close this gap. The GP approach learns a simple yet non-convex data-driven approximation to the AC power flow equations that can incorporate uncertainty inputs. The latter is then used to determine the solution of CC-OPF efficiently, by accounting for both input and parameter uncertainty. The practical efficiency of the proposed approach using different approximations for GP-uncertainty propagation is illustrated over numerous IEEE test cases.