Decoding Quantum LDPC Codes Using Graph Neural Networks

In this paper, we propose a novel decoding method for Quantum Low-Density Parity-Check (QLDPC) codes based on Graph Neural Networks (GNNs). Similar to the Belief Propagation (BP)-based QLDPC decoders, the proposed GNN-based QLDPC decoder exploits the sparse graph structure of QLDPC codes and can be implemented as a message-passing decoding algorithm. We compare the proposed GNN-based decoding algorithm against selected classes of both conventional and neural-enhanced QLDPC decoding algorithms across several QLDPC code designs. The simulation results demonstrate excellent performance of GNN-based decoders along with their low complexity compared to competing methods.

Application of Deep Learning Methods in Monitoring and Optimization of Electric Power Systems

This PhD thesis thoroughly examines the utilization of deep learning techniques as a means to advance the algorithms employed in the monitoring and optimization of electric power systems. The first major contribution of this thesis involves the application of graph neural networks to enhance power system state estimation. The second key aspect of this thesis focuses on utilizing reinforcement learning for dynamic distribution network reconfiguration. The effectiveness of the proposed methods is affirmed through extensive experimentation and simulations.

Graph Neural Networks on Factor Graphs for Robust, Fast, and Scalable Linear State Estimation with PMUs

As phasor measurement units (PMUs) become more widely used in transmission power systems, a fast state estimation (SE) algorithm that can take advantage of their high sample rates is needed. To accomplish this, we present a method that uses graph neural networks (GNNs) to learn complex bus voltage estimates from PMU voltage and current measurements. We propose an original implementation of GNNs over the power system's factor graph to simplify the integration of various types and quantities of measurements on power system buses and branches. Furthermore, we augment the factor graph to improve the robustness of GNN predictions. This model is highly efficient and scalable, as its computational complexity is linear with respect to the number of nodes in the power system. Training and test examples were generated by randomly sampling sets of power system measurements and annotated with the exact solutions of linear SE with PMUs. The numerical results demonstrate that the GNN model provides an accurate approximation of the SE solutions. Furthermore, errors caused by PMU malfunctions or communication failures that would normally make the SE problem unobservable have a local effect and do not deteriorate the results in the rest of the power system.

Scalability and Sample Efficiency Analysis of Graph Neural Networks for Power System State Estimation

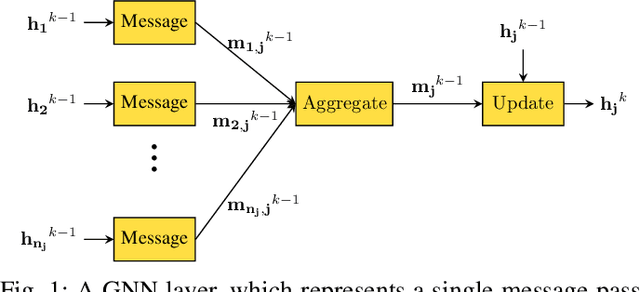
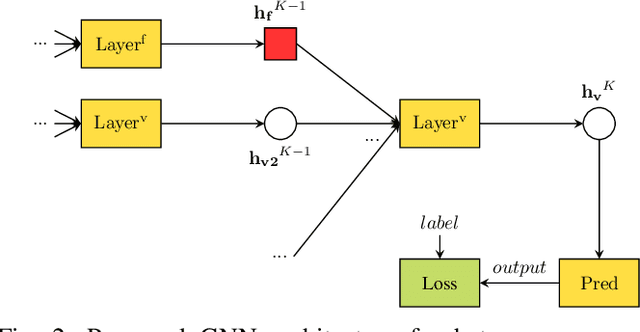
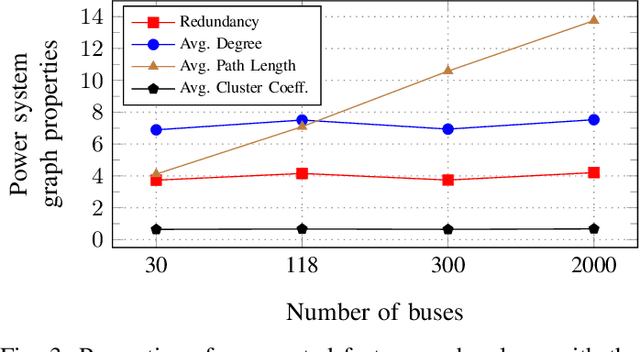
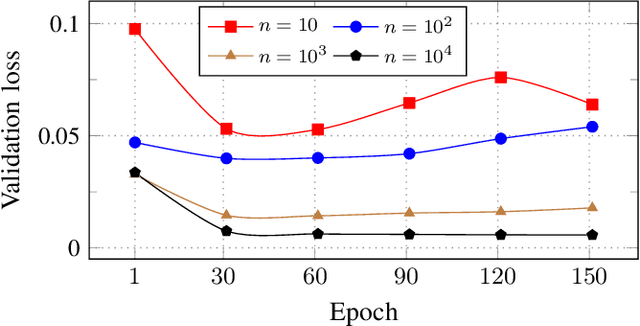
Data-driven state estimation (SE) is becoming increasingly important in modern power systems, as it allows for more efficient analysis of system behaviour using real-time measurement data. This paper thoroughly evaluates a phasor measurement unit-only state estimator based on graph neural networks (GNNs) applied over factor graphs. To assess the sample efficiency of the GNN model, we perform multiple training experiments on various training set sizes. Additionally, to evaluate the scalability of the GNN model, we conduct experiments on power systems of various sizes. Our results show that the GNN-based state estimator exhibits high accuracy and efficient use of data. Additionally, it demonstrated scalability in terms of both memory usage and inference time, making it a promising solution for data-driven SE in modern power systems.

Supporting Future Electrical Utilities: Using Deep Learning Methods in EMS and DMS Algorithms

Electrical power systems are increasing in size, complexity, as well as dynamics due to the growing integration of renewable energy resources, which have sporadic power generation. This necessitates the development of near real-time power system algorithms, demanding lower computational complexity regarding the power system size. Considering the growing trend in the collection of historical measurement data and recent advances in the rapidly developing deep learning field, the main goal of this paper is to provide a review of recent deep learning-based power system monitoring and optimization algorithms. Electrical utilities can benefit from this review by re-implementing or enhancing the algorithms traditionally used in energy management systems (EMS) and distribution management systems (DMS).

GP CC-OPF: Gaussian Process based optimization tool for Chance-Constrained Optimal Power Flow

The Gaussian Process (GP) based Chance-Constrained Optimal Power Flow (CC-OPF) is an open-source Python code developed for solving economic dispatch (ED) problem in modern power grids. In recent years, integrating a significant amount of renewables into a power grid causes high fluctuations and thus brings a lot of uncertainty to power grid operations. This fact makes the conventional model-based CC-OPF problem non-convex and computationally complex to solve. The developed tool presents a novel data-driven approach based on the GP regression model for solving the CC-OPF problem with a trade-off between complexity and accuracy. The proposed approach and developed software can help system operators to effectively perform ED optimization in the presence of large uncertainties in the power grid.

Distributed Nonlinear State Estimation in Electric Power Systems using Graph Neural Networks

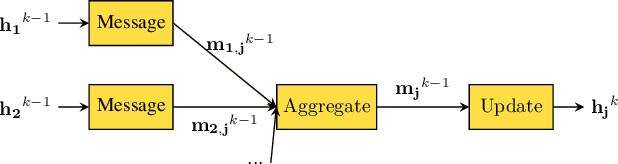
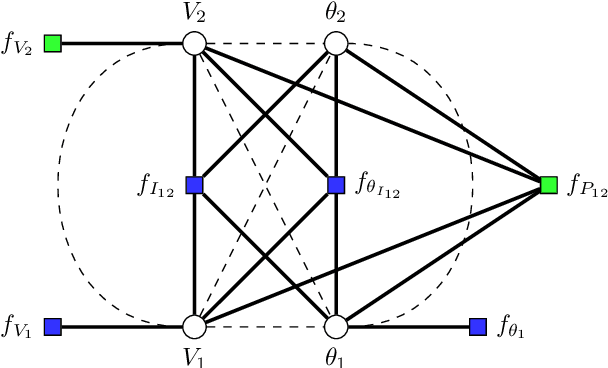
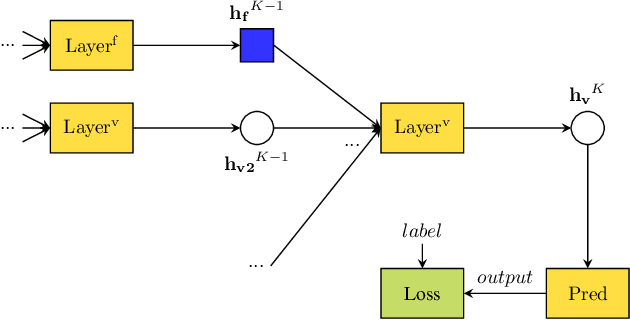
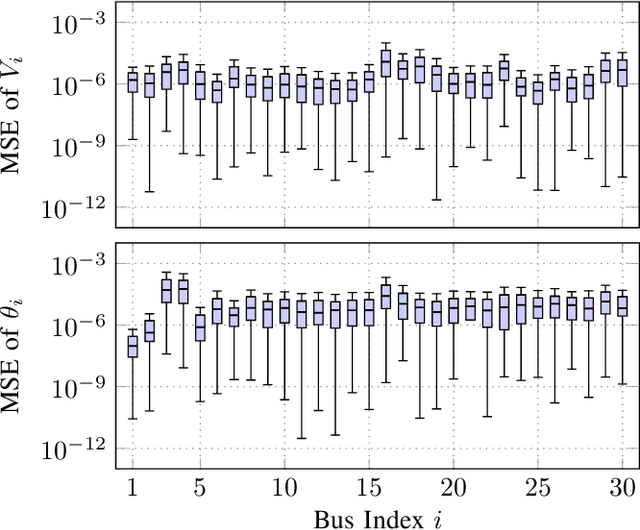
Nonlinear state estimation (SE), with the goal of estimating complex bus voltages based on all types of measurements available in the power system, is usually solved using the iterative Gauss-Newton method. The nonlinear SE presents some difficulties when considering inputs from both phasor measurement units and supervisory control and data acquisition system. These include numerical instabilities, convergence time depending on the starting point of the iterative method, and the quadratic computational complexity of a single iteration regarding the number of state variables. This paper introduces an original graph neural network based SE implementation over the augmented factor graph of the nonlinear power system SE, capable of incorporating measurements on both branches and buses, as well as both phasor and legacy measurements. The proposed regression model has linear computational complexity during the inference time once trained, with a possibility of distributed implementation. Since the method is noniterative and non-matrix-based, it is resilient to the problems that the Gauss-Newton solver is prone to. Aside from prediction accuracy on the test set, the proposed model demonstrates robustness when simulating cyber attacks and unobservable scenarios due to communication irregularities. In those cases, prediction errors are sustained locally, with no effect on the rest of the power system's results.

Near Real-Time Distributed State Estimation via AI/ML-Empowered 5G Networks

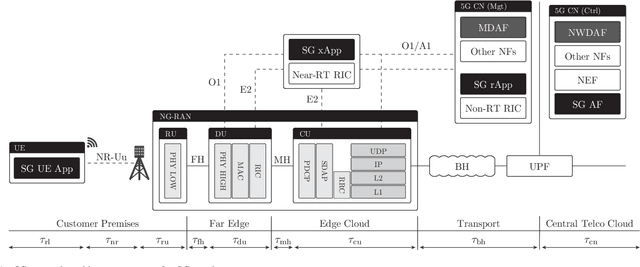
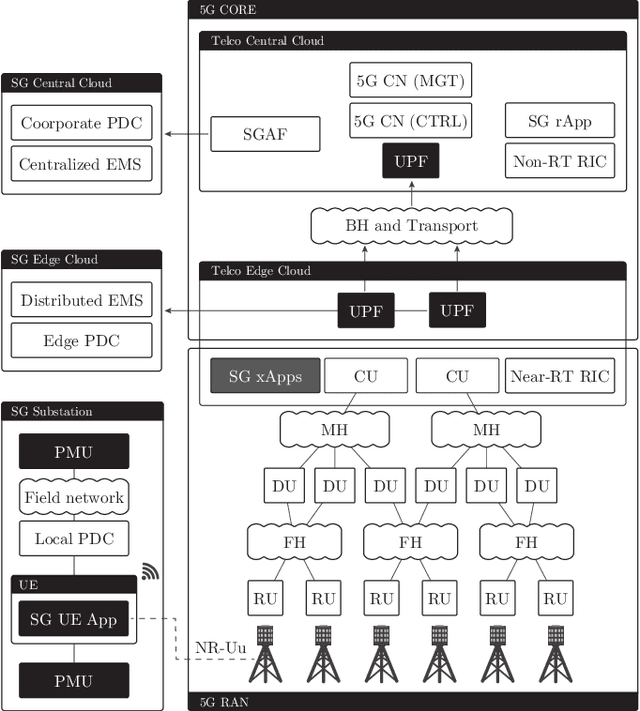
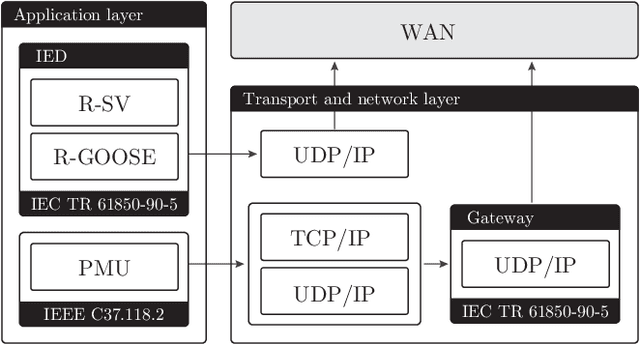
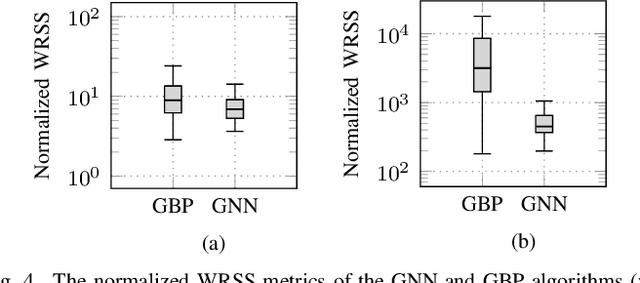
Fifth-Generation (5G) networks have a potential to accelerate power system transition to a flexible, softwarized, data-driven, and intelligent grid. With their evolving support for Machine Learning (ML)/Artificial Intelligence (AI) functions, 5G networks are expected to enable novel data-centric Smart Grid (SG) services. In this paper, we explore how data-driven SG services could be integrated with ML/AI-enabled 5G networks in a symbiotic relationship. We focus on the State Estimation (SE) function as a key element of the energy management system and focus on two main questions. Firstly, in a tutorial fashion, we present an overview on how distributed SE can be integrated with the elements of the 5G core network and radio access network architecture. Secondly, we present and compare two powerful distributed SE methods based on: i) graphical models and belief propagation, and ii) graph neural networks. We discuss their performance and capability to support a near real-time distributed SE via 5G network, taking into account communication delays.

Robust and Fast Data-Driven Power System State Estimator Using Graph Neural Networks

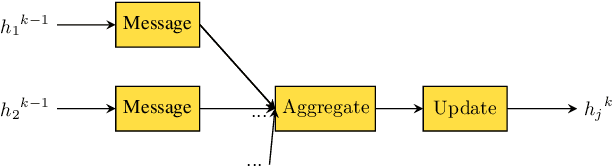
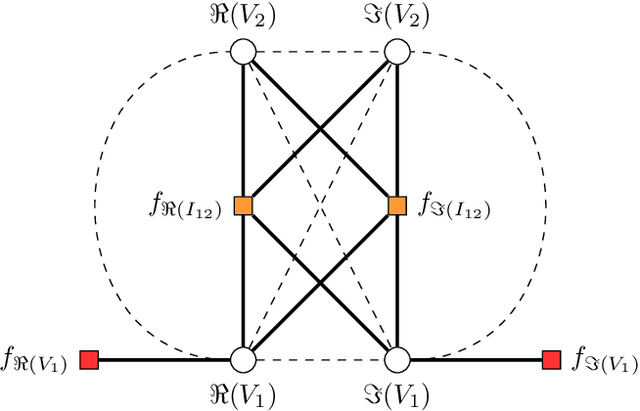
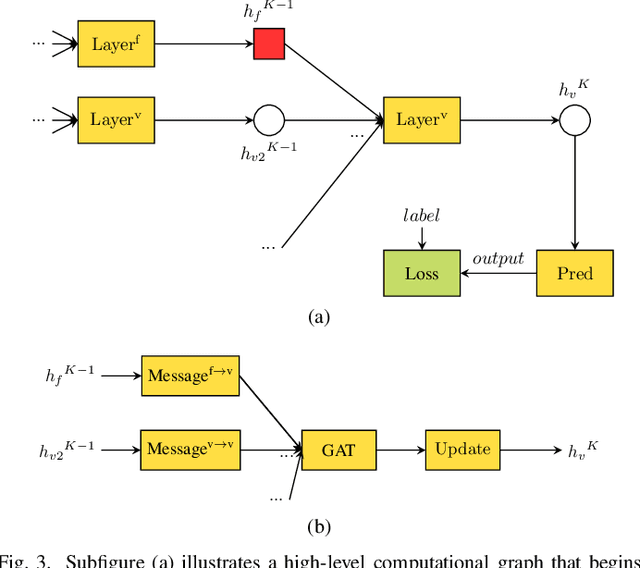
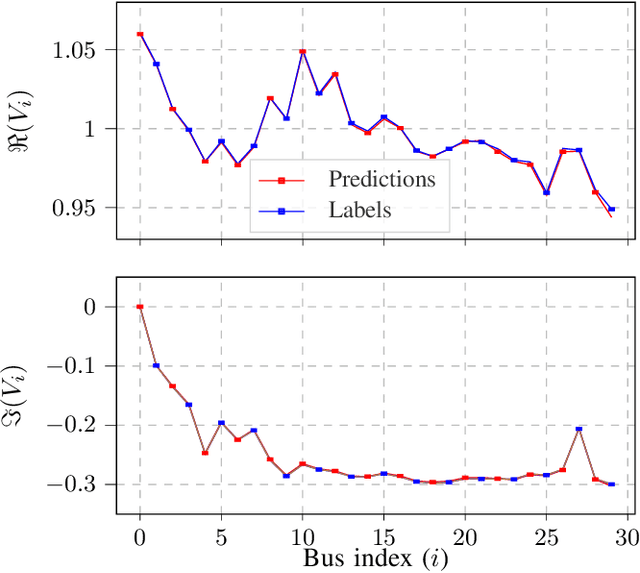
The power system state estimation (SE) algorithm estimates the complex bus voltages based on the available set of measurements. Because phasor measurement units (PMUs) are becoming more widely employed in transmission power systems, a fast SE solver capable of exploiting PMUs' high sample rates is required. To accomplish this, we present a method for training a model based on graph neural networks (GNNs) to learn estimates from PMU voltage and current measurements, which, once it is trained, has a linear computational complexity with respect to the number of nodes in the power system. We propose an original GNN implementation over the power system's factor graph to simplify the incorporation of various types and numbers of measurements both on power system buses and branches. Furthermore, we augment the factor graph to improve the robustness of GNN predictions. Training and test examples were generated by randomly sampling sets of power system measurements and annotated with the exact solutions of linear SE with PMUs. The numerical results demonstrate that the GNN model provides an accurate approximation of the SE solutions. Additionally, errors caused by PMU malfunctions or the communication failures that make the SE problem unobservable have a local effect and do not deteriorate the results in the rest of the power system.

State Estimation in Electric Power Systems Leveraging Graph Neural Networks

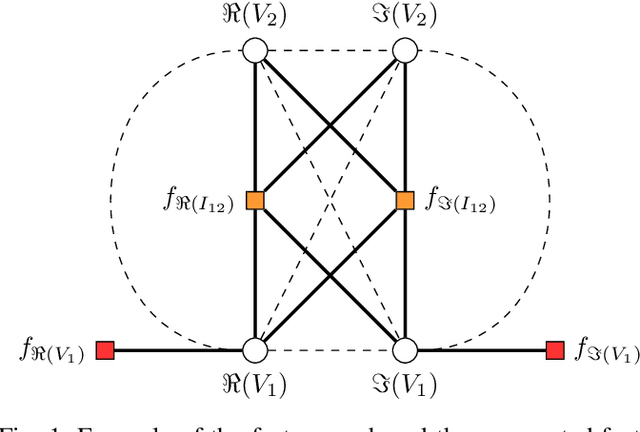
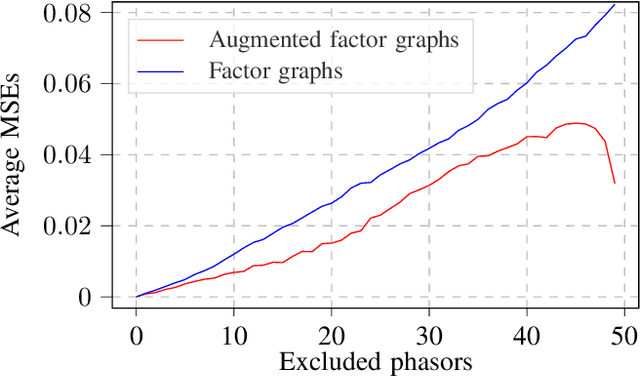
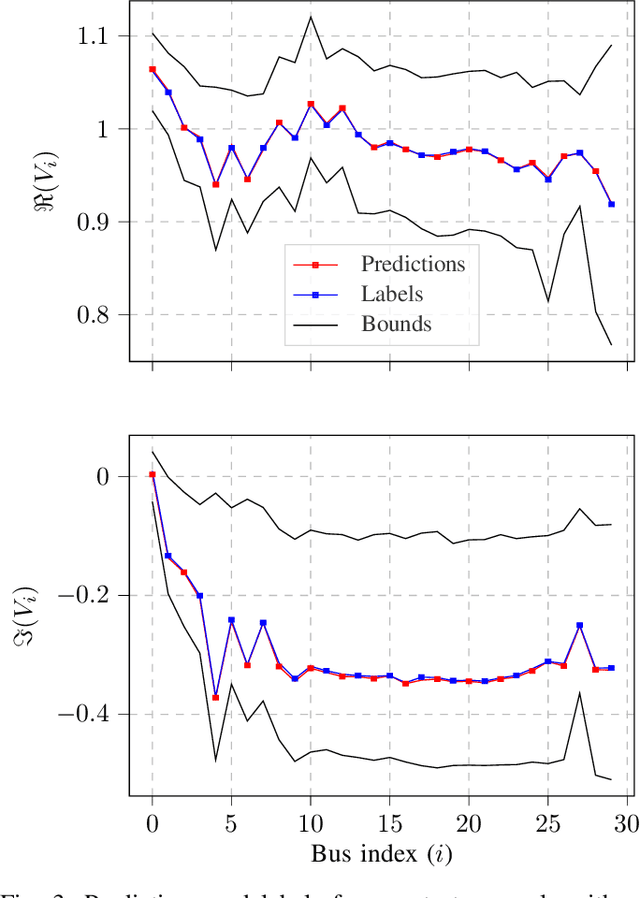
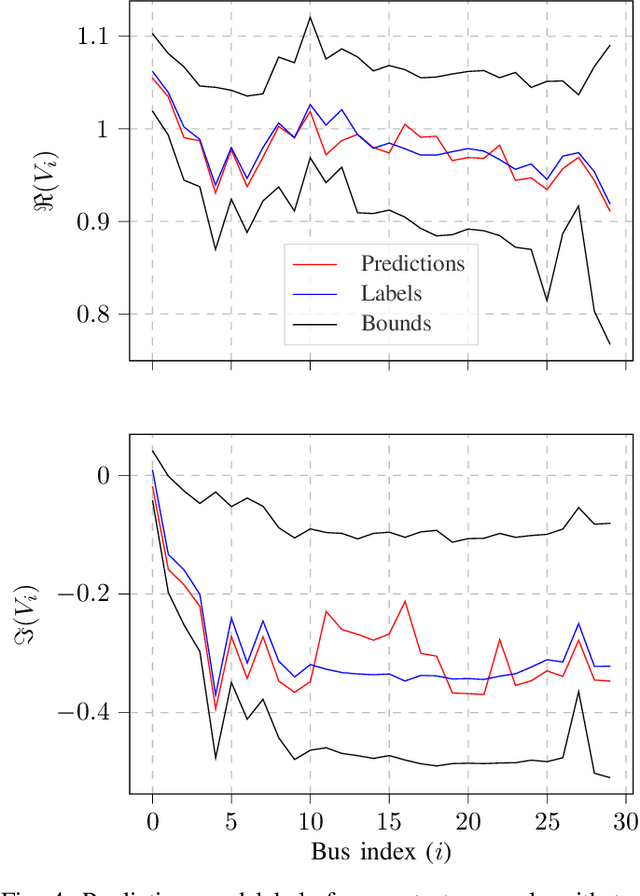
The goal of the state estimation (SE) algorithm is to estimate complex bus voltages as state variables based on the available set of measurements in the power system. Because phasor measurement units (PMUs) are increasingly being used in transmission power systems, there is a need for a fast SE solver that can take advantage of PMU high sampling rates. This paper proposes training a graph neural network (GNN) to learn the estimates given the PMU voltage and current measurements as inputs, with the intent of obtaining fast and accurate predictions during the evaluation phase. GNN is trained using synthetic datasets, created by randomly sampling sets of measurements in the power system and labelling them with a solution obtained using a linear SE with PMUs solver. The presented results display the accuracy of GNN predictions in various test scenarios and tackle the sensitivity of the predictions to the missing input data.