Robust and Fast Data-Driven Power System State Estimator Using Graph Neural Networks
Paper and Code
Jun 06, 2022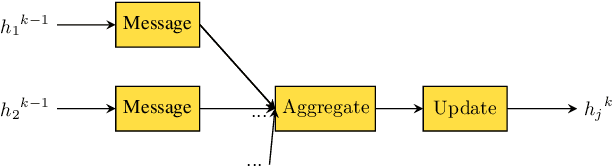
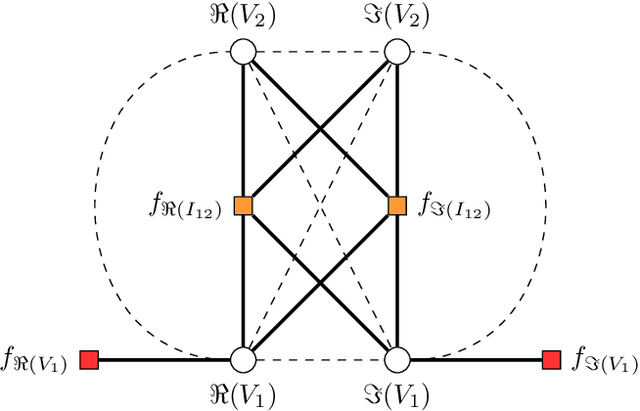
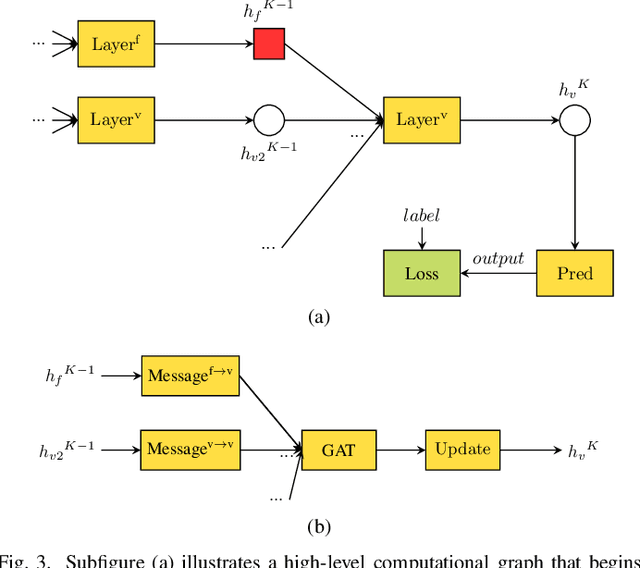
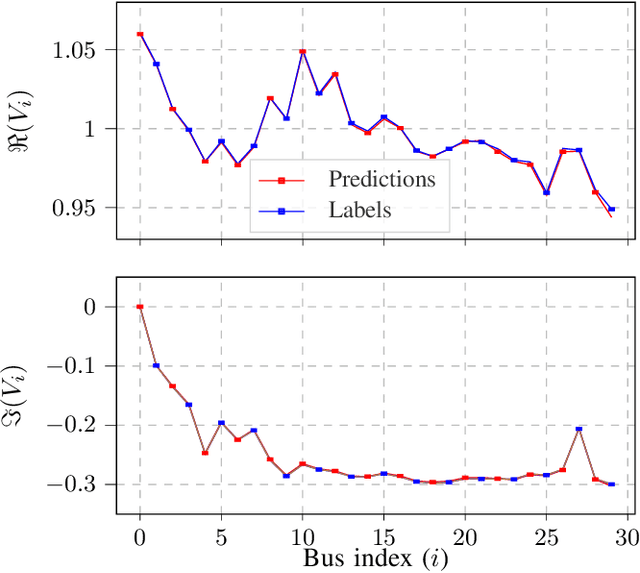
The power system state estimation (SE) algorithm estimates the complex bus voltages based on the available set of measurements. Because phasor measurement units (PMUs) are becoming more widely employed in transmission power systems, a fast SE solver capable of exploiting PMUs' high sample rates is required. To accomplish this, we present a method for training a model based on graph neural networks (GNNs) to learn estimates from PMU voltage and current measurements, which, once it is trained, has a linear computational complexity with respect to the number of nodes in the power system. We propose an original GNN implementation over the power system's factor graph to simplify the incorporation of various types and numbers of measurements both on power system buses and branches. Furthermore, we augment the factor graph to improve the robustness of GNN predictions. Training and test examples were generated by randomly sampling sets of power system measurements and annotated with the exact solutions of linear SE with PMUs. The numerical results demonstrate that the GNN model provides an accurate approximation of the SE solutions. Additionally, errors caused by PMU malfunctions or the communication failures that make the SE problem unobservable have a local effect and do not deteriorate the results in the rest of the power system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge