Rajasekhar Anguluri
Alternating Minimization for Time-Shifted Synergy Extraction in Human Hand Coordination
Dec 20, 2025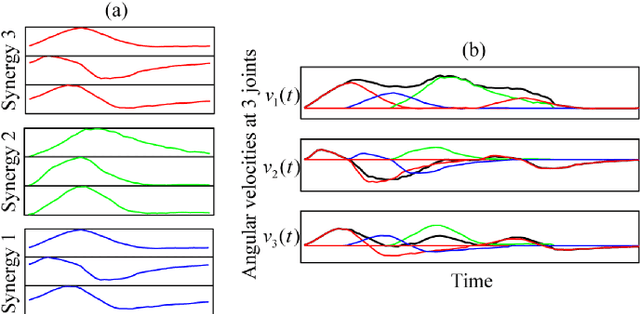
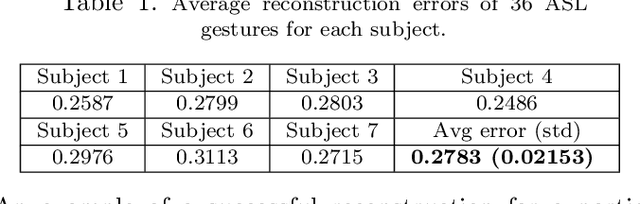
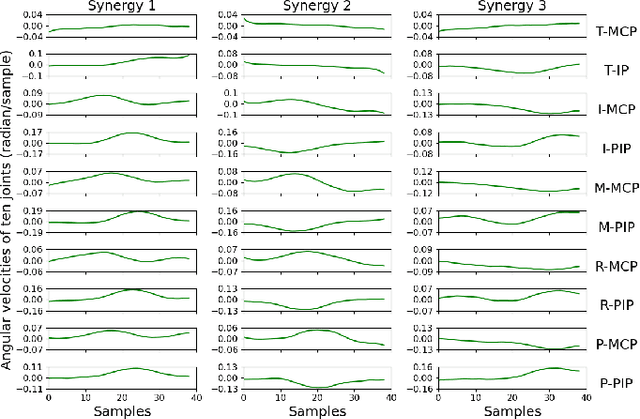
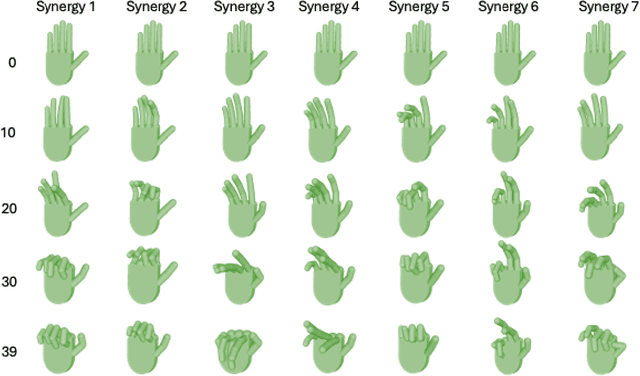
Abstract:Identifying motor synergies -- coordinated hand joint patterns activated at task-dependent time shifts -- from kinematic data is central to motor control and robotics. Existing two-stage methods first extract candidate waveforms (via SVD) and then select shifted templates using sparse optimization, requiring at least two datasets and complicating data collection. We introduce an optimization-based framework that jointly learns a small set of synergies and their sparse activation coefficients. The formulation enforces group sparsity for synergy selection and element-wise sparsity for activation timing. We develop an alternating minimization method in which coefficient updates decouple across tasks and synergy updates reduce to regularized least-squares problems. Our approach requires only a single data set, and simulations show accurate velocity reconstruction with compact, interpretable synergies.
Learning Networks from Wide-Sense Stationary Stochastic Processes
Dec 04, 2024Abstract:Complex networked systems driven by latent inputs are common in fields like neuroscience, finance, and engineering. A key inference problem here is to learn edge connectivity from node outputs (potentials). We focus on systems governed by steady-state linear conservation laws: $X_t = {L^{\ast}}Y_{t}$, where $X_t, Y_t \in \mathbb{R}^p$ denote inputs and potentials, respectively, and the sparsity pattern of the $p \times p$ Laplacian $L^{\ast}$ encodes the edge structure. Assuming $X_t$ to be a wide-sense stationary stochastic process with a known spectral density matrix, we learn the support of $L^{\ast}$ from temporally correlated samples of $Y_t$ via an $\ell_1$-regularized Whittle's maximum likelihood estimator (MLE). The regularization is particularly useful for learning large-scale networks in the high-dimensional setting where the network size $p$ significantly exceeds the number of samples $n$. We show that the MLE problem is strictly convex, admitting a unique solution. Under a novel mutual incoherence condition and certain sufficient conditions on $(n, p, d)$, we show that the ML estimate recovers the sparsity pattern of $L^\ast$ with high probability, where $d$ is the maximum degree of the graph underlying $L^{\ast}$. We provide recovery guarantees for $L^\ast$ in element-wise maximum, Frobenius, and operator norms. Finally, we complement our theoretical results with several simulation studies on synthetic and benchmark datasets, including engineered systems (power and water networks), and real-world datasets from neural systems (such as the human brain).
Robust Model Selection of Non Tree-Structured Gaussian Graphical Models
Nov 10, 2022Abstract:We consider the problem of learning the structure underlying a Gaussian graphical model when the variables (or subsets thereof) are corrupted by independent noise. A recent line of work establishes that even for tree-structured graphical models, only partial structure recovery is possible and goes on to devise algorithms to identify the structure up to an (unavoidable) equivalence class of trees. We extend these results beyond trees and consider the model selection problem under noise for non tree-structured graphs, as tree graphs cannot model several real-world scenarios. Although unidentifiable, we show that, like the tree-structured graphs, the ambiguity is limited to an equivalence class. This limited ambiguity can help provide meaningful clustering information (even with noise), which is helpful in computer and social networks, protein-protein interaction networks, and power networks. Furthermore, we devise an algorithm based on a novel ancestral testing method for recovering the equivalence class. We complement these results with finite sample guarantees for the algorithm in the high-dimensional regime.
Controllability of Coarsely Measured Networked Linear Dynamical Systems (Extended Version)
Jun 21, 2022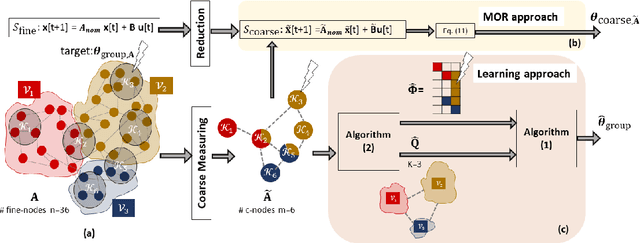
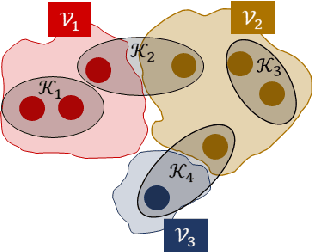
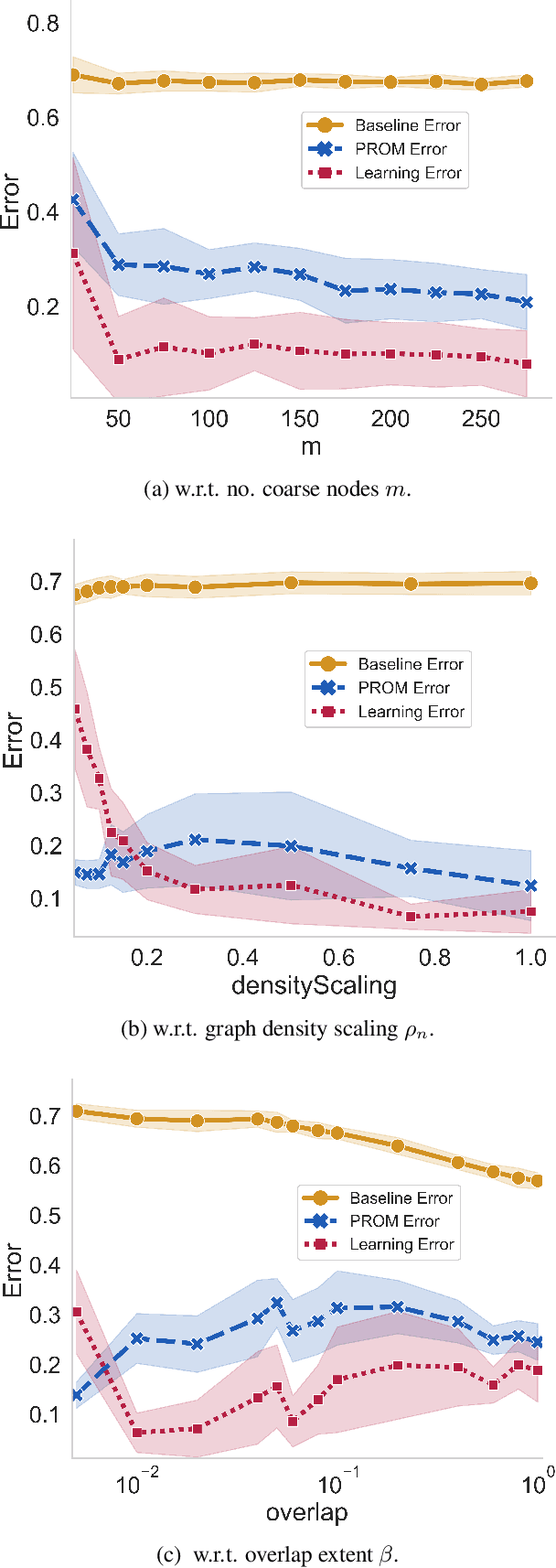
Abstract:We consider the controllability of large-scale linear networked dynamical systems when complete knowledge of network structure is unavailable and knowledge is limited to coarse summaries. We provide conditions under which average controllability of the fine-scale system can be well approximated by average controllability of the (synthesized, reduced-order) coarse-scale system. To this end, we require knowledge of some inherent parametric structure of the fine-scale network that makes this type of approximation possible. Therefore, we assume that the underlying fine-scale network is generated by the stochastic block model (SBM) -- often studied in community detection. We then provide an algorithm that directly estimates the average controllability of the fine-scale system using a coarse summary of SBM. Our analysis indicates the necessity of underlying structure (e.g., in-built communities) to be able to quantify accurately the controllability from coarsely characterized networked dynamics. We also compare our method to that of the reduced-order method and highlight the regimes where both can outperform each other. Finally, we provide simulations to confirm our theoretical results for different scalings of network size and density, and the parameter that captures how much community-structure is retained in the coarse summary.
Learning the Structure of Large Networked Systems Obeying Conservation Laws
Jun 14, 2022
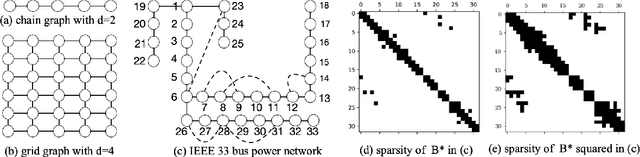
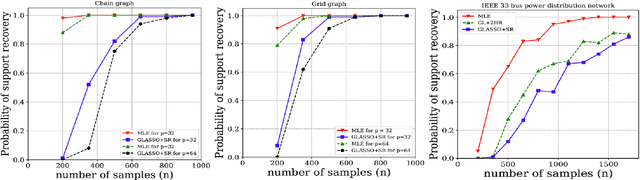
Abstract:Many networked systems such as electric networks, the brain, and social networks of opinion dynamics are known to obey conservation laws. Examples of this phenomenon include the Kirchoff laws in electric networks and opinion consensus in social networks. Conservation laws in networked systems may be modeled as balance equations of the form $X = B^{*} Y$, where the sparsity pattern of $B^{*}$ captures the connectivity of the network, and $Y, X \in \mathbb{R}^p$ are vectors of "potentials" and "injected flows" at the nodes respectively. The node potentials $Y$ cause flows across edges and the flows $X$ injected at the nodes are extraneous to the network dynamics. In several practical systems, the network structure is often unknown and needs to be estimated from data. Towards this, one has access to samples of the node potentials $Y$, but only the statistics of the node injections $X$. Motivated by this important problem, we study the estimation of the sparsity structure of the matrix $B^{*}$ from $n$ samples of $Y$ under the assumption that the node injections $X$ follow a Gaussian distribution with a known covariance $\Sigma_X$. We propose a new $\ell_{1}$-regularized maximum likelihood estimator for this problem in the high-dimensional regime where the size of the network $p$ is larger than sample size $n$. We show that this optimization problem is convex in the objective and admits a unique solution. Under a new mutual incoherence condition, we establish sufficient conditions on the triple $(n,p,d)$ for which exact sparsity recovery of $B^{*}$ is possible with high probability; $d$ is the degree of the graph. We also establish guarantees for the recovery of $B^{*}$ in the element-wise maximum, Frobenius, and operator norms. Finally, we complement these theoretical results with experimental validation of the performance of the proposed estimator on synthetic and real-world data.
On the Robustness of Data-Driven Controllers for Linear Systems
Dec 21, 2019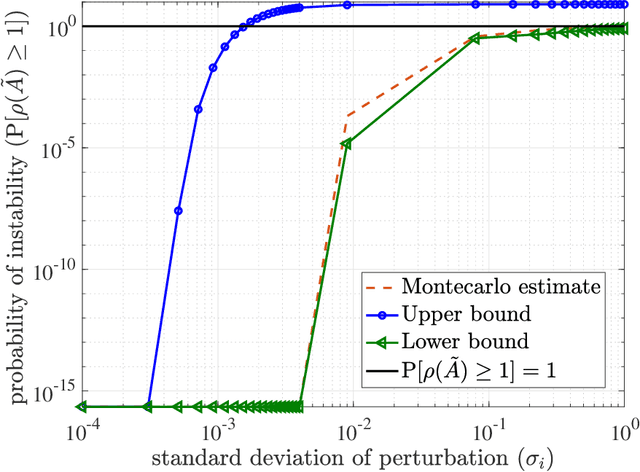
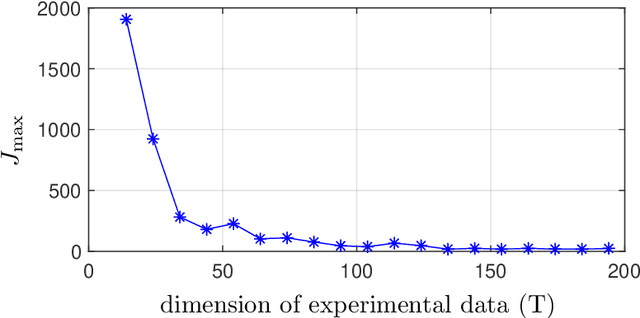
Abstract:This paper proposes a new framework and several results to quantify the performance of data-driven state-feedback controllers for linear systems against targeted perturbations of the training data. We focus on the case where subsets of the training data are randomly corrupted by an adversary, and derive lower and upper bounds for the stability of the closed-loop system with compromised controller as a function of the perturbation statistics, size of the training data, sensitivity of the data-driven algorithm to perturbation of the training data, and properties of the nominal closed-loop system. Our stability and convergence bounds are probabilistic in nature, and rely on a first-order approximation of the data-driven procedure that designs the state-feedback controller, which can be computed directly using the training data. We illustrate our findings via multiple numerical studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge