Controllability of Coarsely Measured Networked Linear Dynamical Systems (Extended Version)

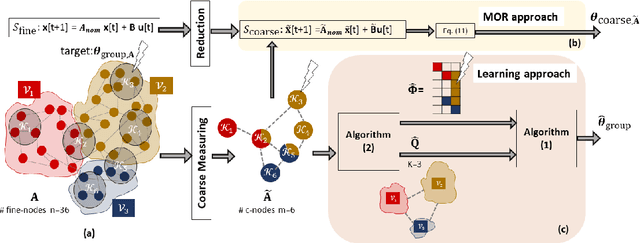
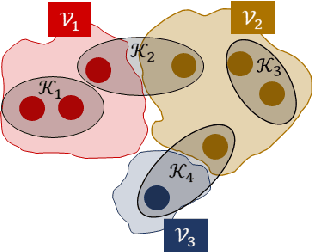
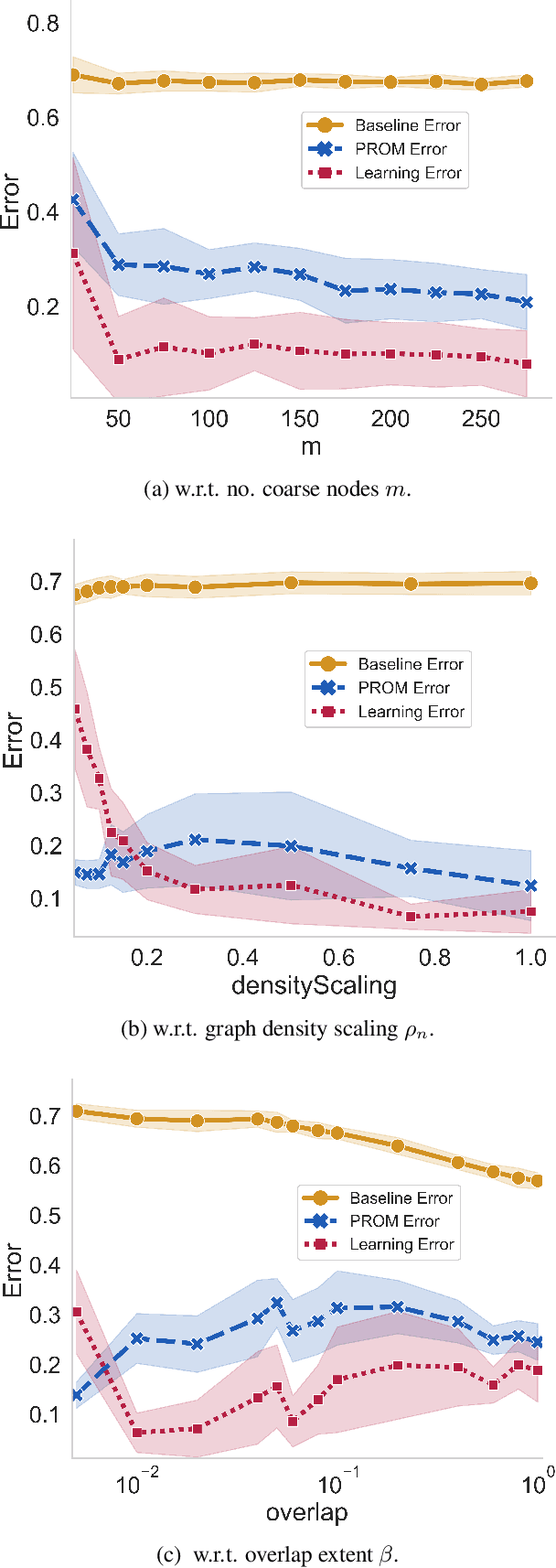
We consider the controllability of large-scale linear networked dynamical systems when complete knowledge of network structure is unavailable and knowledge is limited to coarse summaries. We provide conditions under which average controllability of the fine-scale system can be well approximated by average controllability of the (synthesized, reduced-order) coarse-scale system. To this end, we require knowledge of some inherent parametric structure of the fine-scale network that makes this type of approximation possible. Therefore, we assume that the underlying fine-scale network is generated by the stochastic block model (SBM) -- often studied in community detection. We then provide an algorithm that directly estimates the average controllability of the fine-scale system using a coarse summary of SBM. Our analysis indicates the necessity of underlying structure (e.g., in-built communities) to be able to quantify accurately the controllability from coarsely characterized networked dynamics. We also compare our method to that of the reduced-order method and highlight the regimes where both can outperform each other. Finally, we provide simulations to confirm our theoretical results for different scalings of network size and density, and the parameter that captures how much community-structure is retained in the coarse summary.

Graph Community Detection from Coarse Measurements: Recovery Conditions for the Coarsened Weighted Stochastic Block Model

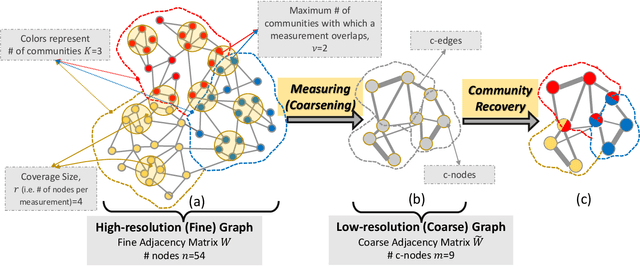
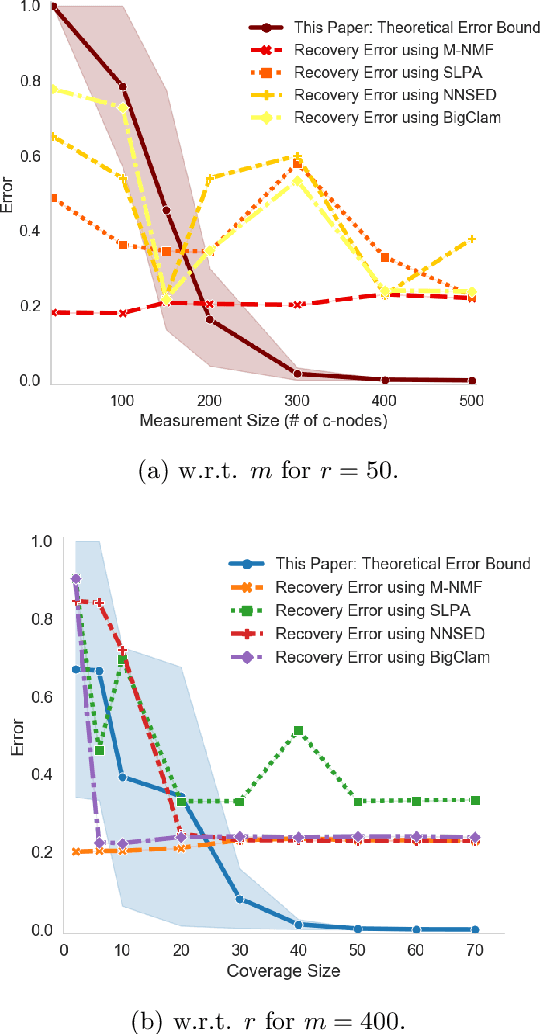
We study the problem of community recovery from coarse measurements of a graph. In contrast to the problem of community recovery of a fully observed graph, one often encounters situations when measurements of a graph are made at low-resolution, each measurement integrating across multiple graph nodes. Such low-resolution measurements effectively induce a coarse graph with its own communities. Our objective is to develop conditions on the graph structure, the quantity, and properties of measurements, under which we can recover the community organization in this coarse graph. In this paper, we build on the stochastic block model by mathematically formalizing the coarsening process, and characterizing its impact on the community members and connections. Through this novel setup and modeling, we characterize an error bound for community recovery. The error bound yields simple and closed-form asymptotic conditions to achieve the perfect recovery of the coarse graph communities.

Node-Centric Graph Learning from Data for Brain State Identification

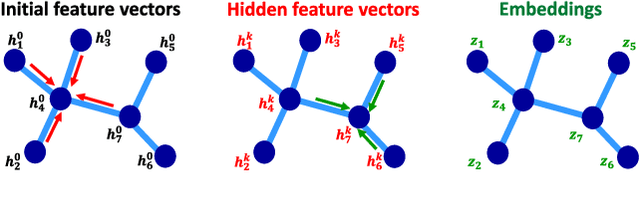
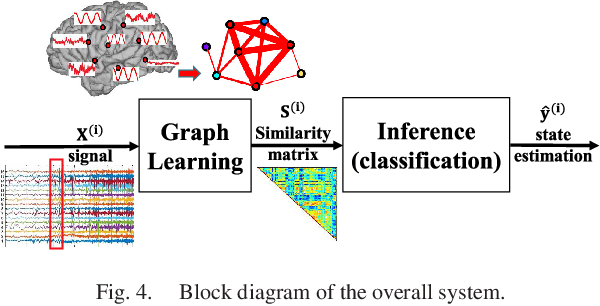
Data-driven graph learning models a network by determining the strength of connections between its nodes. The data refers to a graph signal which associates a value with each graph node. Existing graph learning methods either use simplified models for the graph signal, or they are prohibitively expensive in terms of computational and memory requirements. This is particularly true when the number of nodes is high or there are temporal changes in the network. In order to consider richer models with a reasonable computational tractability, we introduce a graph learning method based on representation learning on graphs. Representation learning generates an embedding for each graph node, taking the information from neighbouring nodes into account. Our graph learning method further modifies the embeddings to compute the graph similarity matrix. In this work, graph learning is used to examine brain networks for brain state identification. We infer time-varying brain graphs from an extensive dataset of intracranial electroencephalographic (iEEG) signals from ten patients. We then apply the graphs as input to a classifier to distinguish seizure vs. non-seizure brain states. Using the binary classification metric of area under the receiver operating characteristic curve (AUC), this approach yields an average of 9.13 percent improvement when compared to two widely used brain network modeling methods.

A Hierarchical Graph Signal Processing Approach to Inference from Spatiotemporal Signals

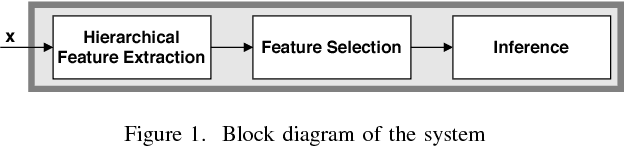
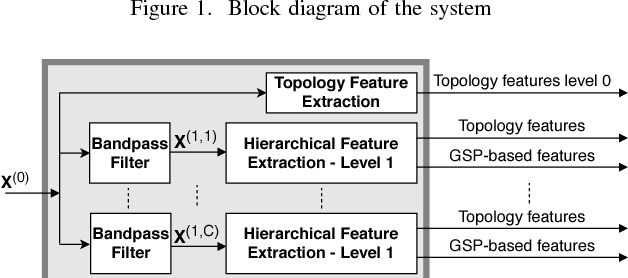
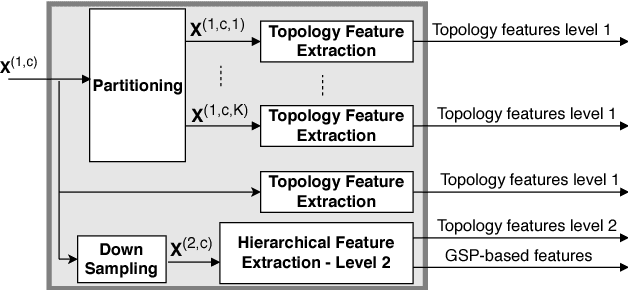
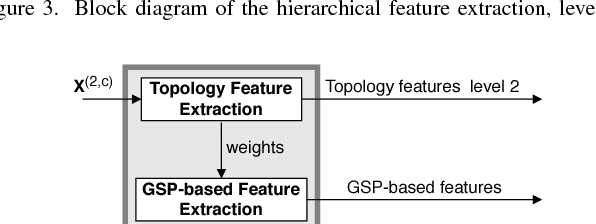
Motivated by the emerging area of graph signal processing (GSP), we introduce a novel method to draw inference from spatiotemporal signals. Data acquisition in different locations over time is common in sensor networks, for diverse applications ranging from object tracking in wireless networks to medical uses such as electroencephalography (EEG) signal processing. In this paper we leverage novel techniques of GSP to develop a hierarchical feature extraction approach by mapping the data onto a series of spatiotemporal graphs. Such a model maps signals onto vertices of a graph and the time-space dependencies among signals are modeled by the edge weights. Signal components acquired from different locations and time often have complicated functional dependencies. Accordingly, their corresponding graph weights are learned from data and used in two ways. First, they are used as a part of the embedding related to the topology of graph, such as density. Second, they provide the connectivities of the base graph for extracting higher level GSP-based features. The latter include the energies of the signal's graph Fourier transform in different frequency bands. We test our approach on the intracranial EEG (iEEG) data set of the Kaggle epileptic seizure detection contest. In comparison to the winning code, the results show a slight net improvement and up to 6 percent improvement in per subject analysis, while the number of features are decreased by 75 percent on average.