A Hierarchical Graph Signal Processing Approach to Inference from Spatiotemporal Signals

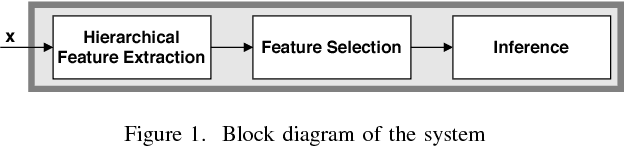
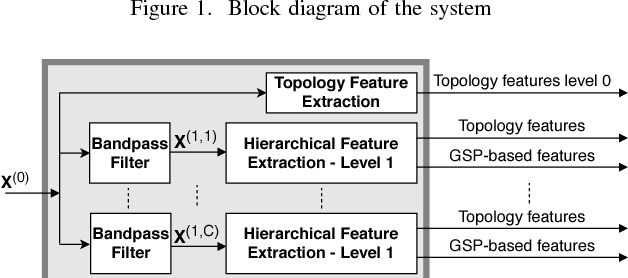
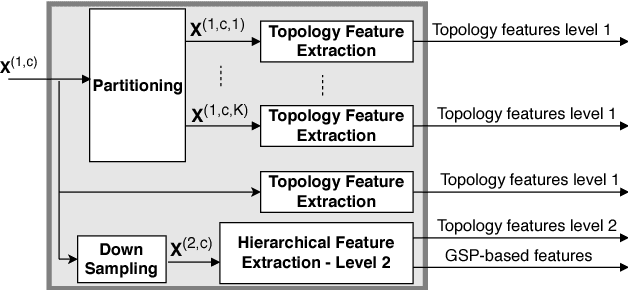
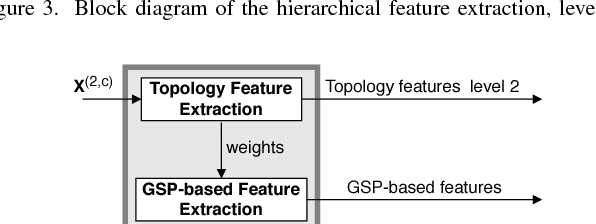
Motivated by the emerging area of graph signal processing (GSP), we introduce a novel method to draw inference from spatiotemporal signals. Data acquisition in different locations over time is common in sensor networks, for diverse applications ranging from object tracking in wireless networks to medical uses such as electroencephalography (EEG) signal processing. In this paper we leverage novel techniques of GSP to develop a hierarchical feature extraction approach by mapping the data onto a series of spatiotemporal graphs. Such a model maps signals onto vertices of a graph and the time-space dependencies among signals are modeled by the edge weights. Signal components acquired from different locations and time often have complicated functional dependencies. Accordingly, their corresponding graph weights are learned from data and used in two ways. First, they are used as a part of the embedding related to the topology of graph, such as density. Second, they provide the connectivities of the base graph for extracting higher level GSP-based features. The latter include the energies of the signal's graph Fourier transform in different frequency bands. We test our approach on the intracranial EEG (iEEG) data set of the Kaggle epileptic seizure detection contest. In comparison to the winning code, the results show a slight net improvement and up to 6 percent improvement in per subject analysis, while the number of features are decreased by 75 percent on average.