Quasicyclic Principal Component Analysis

We present quasicyclic principal component analysis (QPCA), a generalization of principal component analysis (PCA), that determines an optimized basis for a dataset in terms of families of shift-orthogonal principal vectors. This is of particular interest when analyzing cyclostationary data, whose cyclic structure is not exploited by the standard PCA algorithm. We first formulate QPCA as an optimization problem, which we show may be decomposed into a series of PCA problems in the frequency domain. We then formalize our solution as an explicit algorithm and analyze its computational complexity. Finally, we provide some examples of applications of QPCA to cyclostationary signal processing data, including an investigation of carrier pulse recovery, a presentation of methods for estimating an unknown oversampling rate, and a discussion of an appropriate approach for pre-processing data with a non-integer oversampling rate in order to better apply the QPCA algorithm.

Controllability of Coarsely Measured Networked Linear Dynamical Systems (Extended Version)

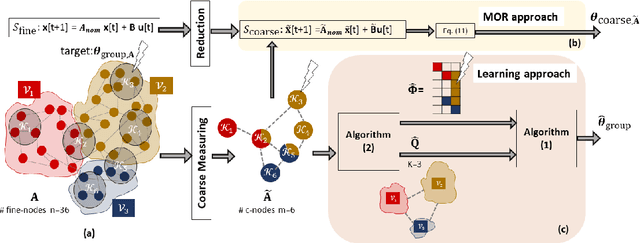
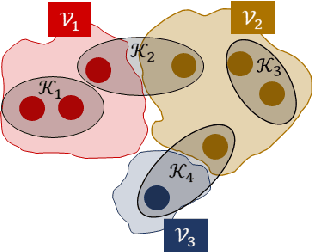
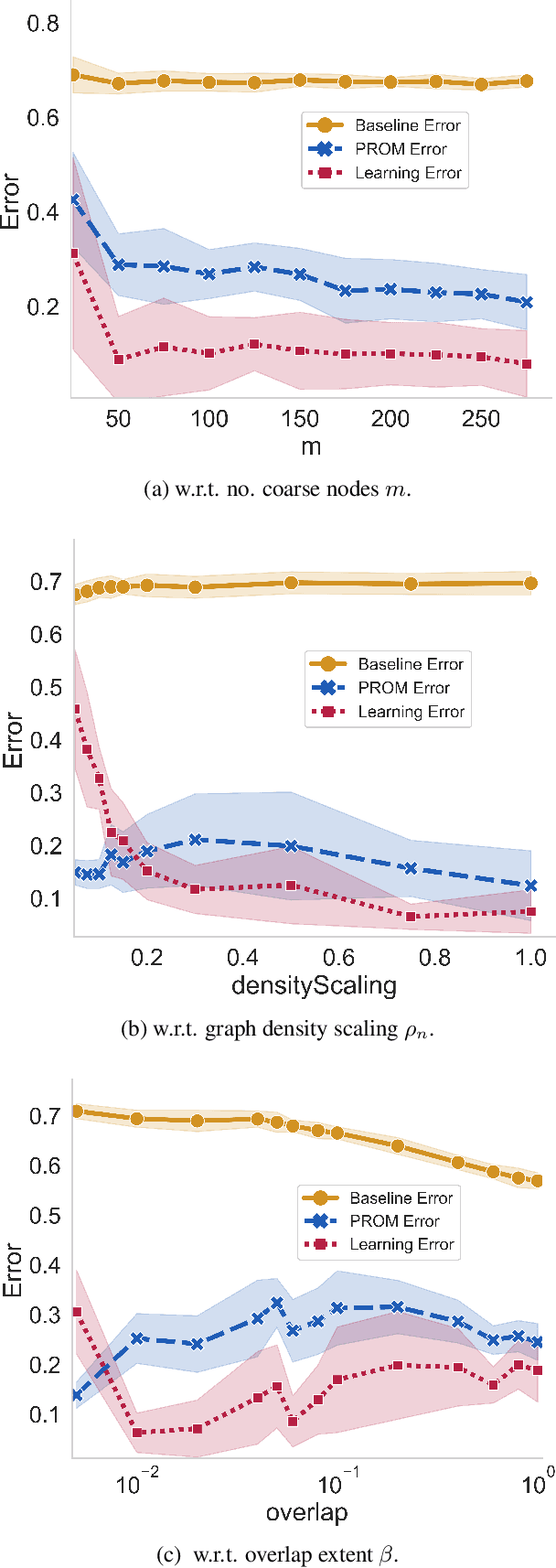
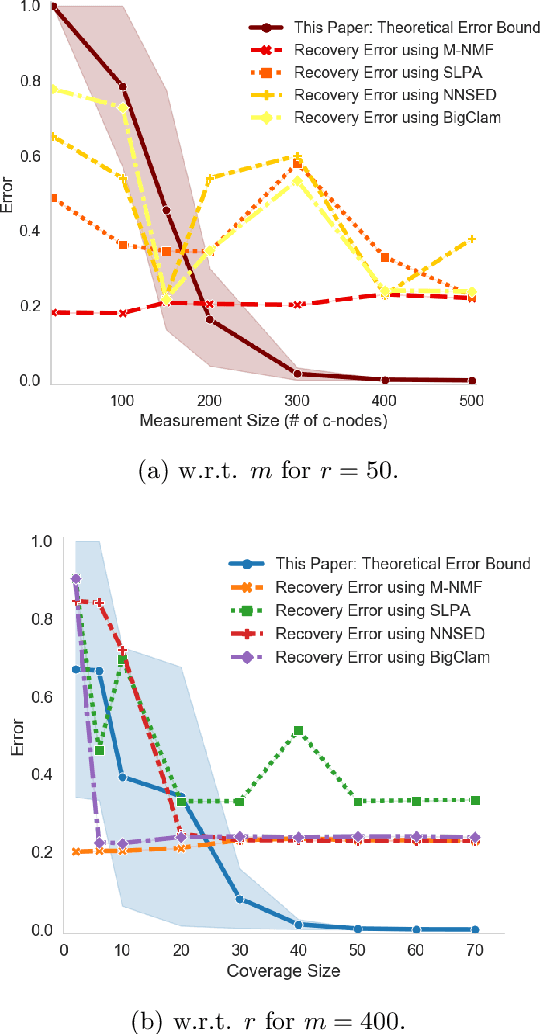
We consider the controllability of large-scale linear networked dynamical systems when complete knowledge of network structure is unavailable and knowledge is limited to coarse summaries. We provide conditions under which average controllability of the fine-scale system can be well approximated by average controllability of the (synthesized, reduced-order) coarse-scale system. To this end, we require knowledge of some inherent parametric structure of the fine-scale network that makes this type of approximation possible. Therefore, we assume that the underlying fine-scale network is generated by the stochastic block model (SBM) -- often studied in community detection. We then provide an algorithm that directly estimates the average controllability of the fine-scale system using a coarse summary of SBM. Our analysis indicates the necessity of underlying structure (e.g., in-built communities) to be able to quantify accurately the controllability from coarsely characterized networked dynamics. We also compare our method to that of the reduced-order method and highlight the regimes where both can outperform each other. Finally, we provide simulations to confirm our theoretical results for different scalings of network size and density, and the parameter that captures how much community-structure is retained in the coarse summary.

Compressing gradients by exploiting temporal correlation in momentum-SGD

An increasing bottleneck in decentralized optimization is communication. Bigger models and growing datasets mean that decentralization of computation is important and that the amount of information exchanged is quickly growing. While compression techniques have been introduced to cope with the latter, none has considered leveraging the temporal correlations that exist in consecutive vector updates. An important example is distributed momentum-SGD where temporal correlation is enhanced by the low-pass-filtering effect of applying momentum. In this paper we design and analyze compression methods that exploit temporal correlation in systems both with and without error-feedback. Experiments with the ImageNet dataset demonstrate that our proposed methods offer significant reduction in the rate of communication at only a negligible increase in computation complexity. We further analyze the convergence of SGD when compression is applied with error-feedback. In the literature, convergence guarantees are developed only for compressors that provide error-bounds point-wise, i.e., for each input to the compressor. In contrast, many important codes (e.g. rate-distortion codes) provide error-bounds only in expectation and thus provide a more general guarantee. In this paper we prove the convergence of SGD under an expected error assumption by establishing a bound for the minimum gradient norm.

Uncertainty-Aware Learning for Improvements in Image Quality of the Canada-France-Hawaii Telescope

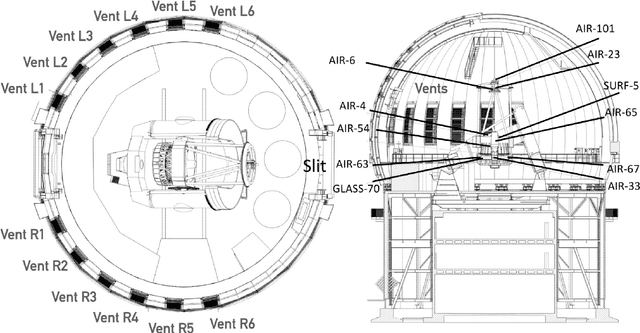
We leverage state-of-the-art machine learning methods and a decade's worth of archival data from the Canada-France-Hawaii Telescope (CFHT) to predict observatory image quality (IQ) from environmental conditions and observatory operating parameters. Specifically, we develop accurate and interpretable models of the complex dependence between data features and observed IQ for CFHT's wide field camera, MegaCam. Our contributions are several-fold. First, we collect, collate and reprocess several disparate data sets gathered by CFHT scientists. Second, we predict probability distribution functions (PDFs) of IQ, and achieve a mean absolute error of $\sim0.07''$ for the predicted medians. Third, we explore data-driven actuation of the 12 dome ``vents'', installed in 2013-14 to accelerate the flushing of hot air from the dome. We leverage epistemic and aleatoric uncertainties in conjunction with probabilistic generative modeling to identify candidate vent adjustments that are in-distribution (ID) and, for the optimal configuration for each ID sample, we predict the reduction in required observing time to achieve a fixed SNR. On average, the reduction is $\sim15\%$. Finally, we rank sensor data features by Shapley values to identify the most predictive variables for each observation. Our long-term goal is to construct reliable and real-time models that can forecast optimal observatory operating parameters for optimization of IQ. Such forecasts can then be fed into scheduling protocols and predictive maintenance routines. We anticipate that such approaches will become standard in automating observatory operations and maintenance by the time CFHT's successor, the Maunakea Spectroscopic Explorer (MSE), is installed in the next decade.

Graph Community Detection from Coarse Measurements: Recovery Conditions for the Coarsened Weighted Stochastic Block Model

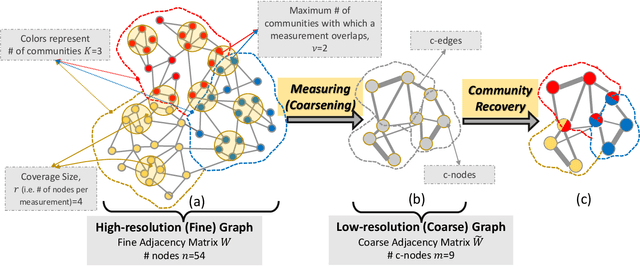
We study the problem of community recovery from coarse measurements of a graph. In contrast to the problem of community recovery of a fully observed graph, one often encounters situations when measurements of a graph are made at low-resolution, each measurement integrating across multiple graph nodes. Such low-resolution measurements effectively induce a coarse graph with its own communities. Our objective is to develop conditions on the graph structure, the quantity, and properties of measurements, under which we can recover the community organization in this coarse graph. In this paper, we build on the stochastic block model by mathematically formalizing the coarsening process, and characterizing its impact on the community members and connections. Through this novel setup and modeling, we characterize an error bound for community recovery. The error bound yields simple and closed-form asymptotic conditions to achieve the perfect recovery of the coarse graph communities.

Node-Centric Graph Learning from Data for Brain State Identification

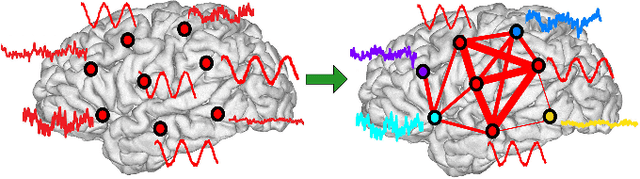
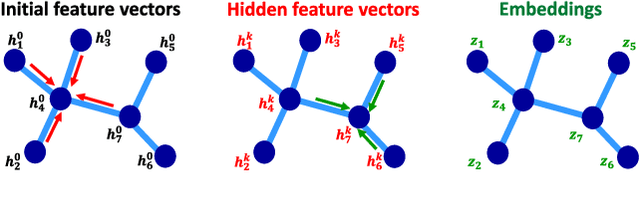
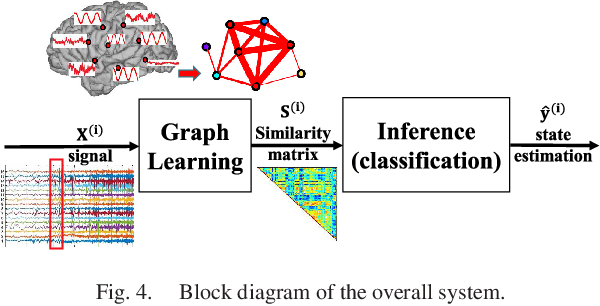
Data-driven graph learning models a network by determining the strength of connections between its nodes. The data refers to a graph signal which associates a value with each graph node. Existing graph learning methods either use simplified models for the graph signal, or they are prohibitively expensive in terms of computational and memory requirements. This is particularly true when the number of nodes is high or there are temporal changes in the network. In order to consider richer models with a reasonable computational tractability, we introduce a graph learning method based on representation learning on graphs. Representation learning generates an embedding for each graph node, taking the information from neighbouring nodes into account. Our graph learning method further modifies the embeddings to compute the graph similarity matrix. In this work, graph learning is used to examine brain networks for brain state identification. We infer time-varying brain graphs from an extensive dataset of intracranial electroencephalographic (iEEG) signals from ten patients. We then apply the graphs as input to a classifier to distinguish seizure vs. non-seizure brain states. Using the binary classification metric of area under the receiver operating characteristic curve (AUC), this approach yields an average of 9.13 percent improvement when compared to two widely used brain network modeling methods.

A Hierarchical Graph Signal Processing Approach to Inference from Spatiotemporal Signals

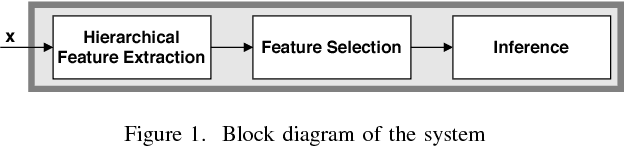
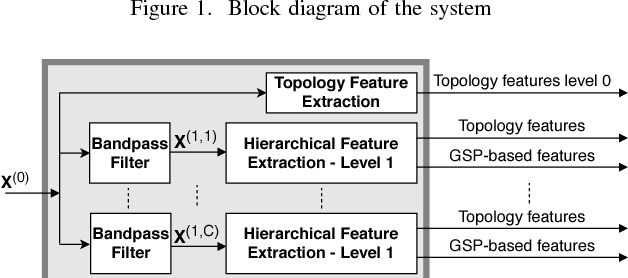
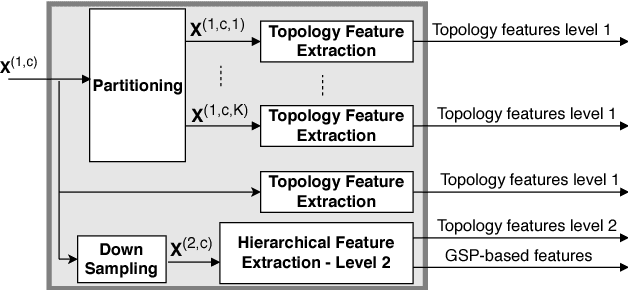
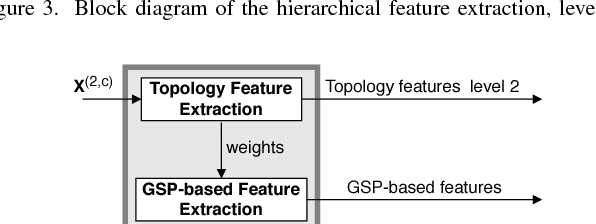
Motivated by the emerging area of graph signal processing (GSP), we introduce a novel method to draw inference from spatiotemporal signals. Data acquisition in different locations over time is common in sensor networks, for diverse applications ranging from object tracking in wireless networks to medical uses such as electroencephalography (EEG) signal processing. In this paper we leverage novel techniques of GSP to develop a hierarchical feature extraction approach by mapping the data onto a series of spatiotemporal graphs. Such a model maps signals onto vertices of a graph and the time-space dependencies among signals are modeled by the edge weights. Signal components acquired from different locations and time often have complicated functional dependencies. Accordingly, their corresponding graph weights are learned from data and used in two ways. First, they are used as a part of the embedding related to the topology of graph, such as density. Second, they provide the connectivities of the base graph for extracting higher level GSP-based features. The latter include the energies of the signal's graph Fourier transform in different frequency bands. We test our approach on the intracranial EEG (iEEG) data set of the Kaggle epileptic seizure detection contest. In comparison to the winning code, the results show a slight net improvement and up to 6 percent improvement in per subject analysis, while the number of features are decreased by 75 percent on average.

Anytime MiniBatch: Exploiting Stragglers in Online Distributed Optimization

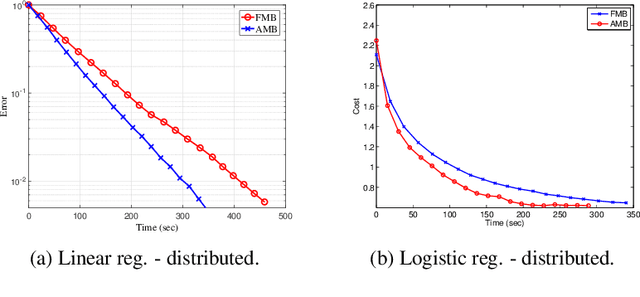
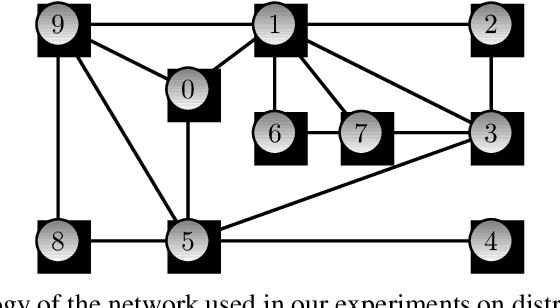
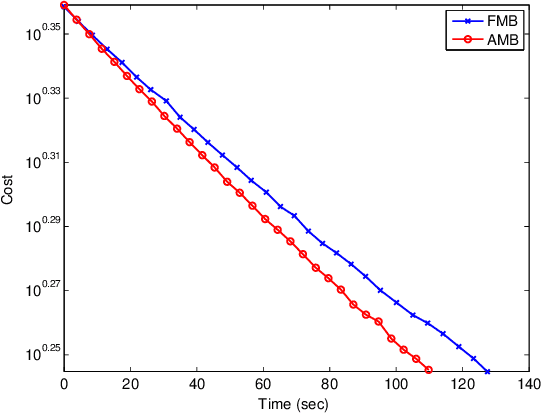
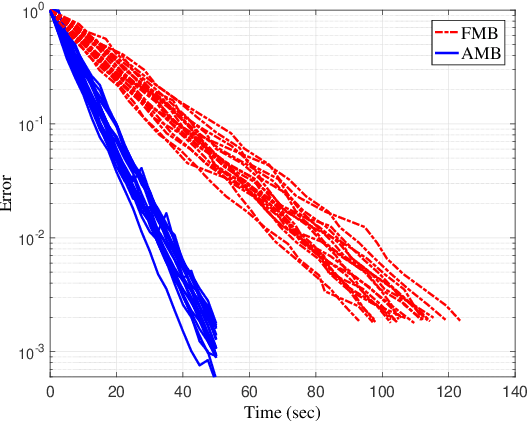
Distributed optimization is vital in solving large-scale machine learning problems. A widely-shared feature of distributed optimization techniques is the requirement that all nodes complete their assigned tasks in each computational epoch before the system can proceed to the next epoch. In such settings, slow nodes, called stragglers, can greatly slow progress. To mitigate the impact of stragglers, we propose an online distributed optimization method called Anytime Minibatch. In this approach, all nodes are given a fixed time to compute the gradients of as many data samples as possible. The result is a variable per-node minibatch size. Workers then get a fixed communication time to average their minibatch gradients via several rounds of consensus, which are then used to update primal variables via dual averaging. Anytime Minibatch prevents stragglers from holding up the system without wasting the work that stragglers can complete. We present a convergence analysis and analyze the wall time performance. Our numerical results show that our approach is up to 1.5 times faster in Amazon EC2 and it is up to five times faster when there is greater variability in compute node performance.

Efficient learning of neighbor representations for boundary trees and forests

We introduce a semiparametric approach to neighbor-based classification. We build off the recently proposed Boundary Trees algorithm by Mathy et al.(2015) which enables fast neighbor-based classification, regression and retrieval in large datasets. While boundary trees use an Euclidean measure of similarity, the Differentiable Boundary Tree algorithm by Zoran et al.(2017) was introduced to learn low-dimensional representations of complex input data, on which semantic similarity can be calculated to train boundary trees. As is pointed out by its authors, the differentiable boundary tree approach contains a few limitations that prevents it from scaling to large datasets. In this paper, we introduce Differentiable Boundary Sets, an algorithm that overcomes the computational issues of the differentiable boundary tree scheme and also improves its classification accuracy and data representability. Our algorithm is efficiently implementable with existing tools and offers a significant reduction in training time. We test and compare the algorithms on the well known MNIST handwritten digits dataset and the newer Fashion-MNIST dataset by Xiao et al.(2017).

Rank Minimization over Finite Fields: Fundamental Limits and Coding-Theoretic Interpretations

This paper establishes information-theoretic limits in estimating a finite field low-rank matrix given random linear measurements of it. These linear measurements are obtained by taking inner products of the low-rank matrix with random sensing matrices. Necessary and sufficient conditions on the number of measurements required are provided. It is shown that these conditions are sharp and the minimum-rank decoder is asymptotically optimal. The reliability function of this decoder is also derived by appealing to de Caen's lower bound on the probability of a union. The sufficient condition also holds when the sensing matrices are sparse - a scenario that may be amenable to efficient decoding. More precisely, it is shown that if the n\times n-sensing matrices contain, on average, \Omega(nlog n) entries, the number of measurements required is the same as that when the sensing matrices are dense and contain entries drawn uniformly at random from the field. Analogies are drawn between the above results and rank-metric codes in the coding theory literature. In fact, we are also strongly motivated by understanding when minimum rank distance decoding of random rank-metric codes succeeds. To this end, we derive distance properties of equiprobable and sparse rank-metric codes. These distance properties provide a precise geometric interpretation of the fact that the sparse ensemble requires as few measurements as the dense one. Finally, we provide a non-exhaustive procedure to search for the unknown low-rank matrix.