Information-Theoretic Bayes Risk Lower Bounds for Realizable Models

We derive information-theoretic lower bounds on the Bayes risk and generalization error of realizable machine learning models. In particular, we employ an analysis in which the rate-distortion function of the model parameters bounds the required mutual information between the training samples and the model parameters in order to learn a model up to a Bayes risk constraint. For realizable models, we show that both the rate distortion function and mutual information admit expressions that are convenient for analysis. For models that are (roughly) lower Lipschitz in their parameters, we bound the rate distortion function from below, whereas for VC classes, the mutual information is bounded above by $d_\mathrm{vc}\log(n)$. When these conditions match, the Bayes risk with respect to the zero-one loss scales no faster than $\Omega(d_\mathrm{vc}/n)$, which matches known outer bounds and minimax lower bounds up to logarithmic factors. We also consider the impact of label noise, providing lower bounds when training and/or test samples are corrupted.

Anytime MiniBatch: Exploiting Stragglers in Online Distributed Optimization

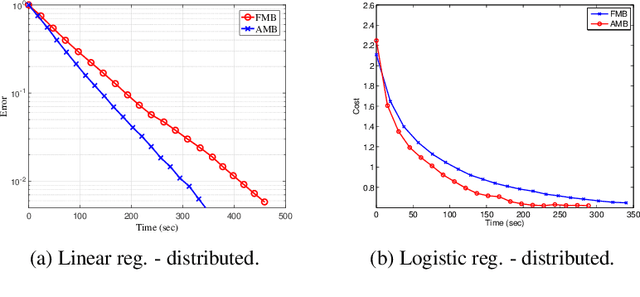
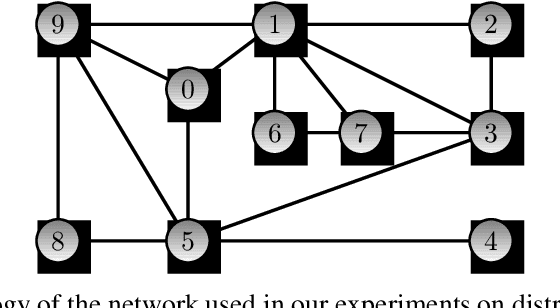
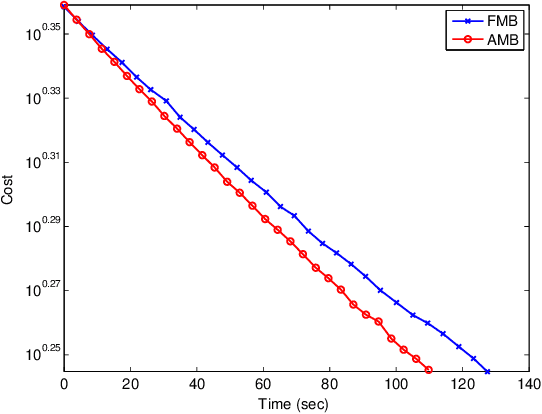
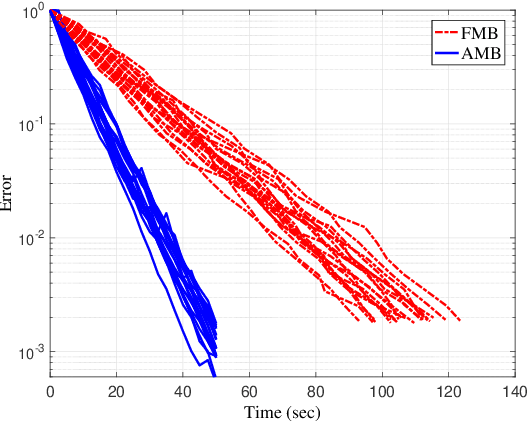
Distributed optimization is vital in solving large-scale machine learning problems. A widely-shared feature of distributed optimization techniques is the requirement that all nodes complete their assigned tasks in each computational epoch before the system can proceed to the next epoch. In such settings, slow nodes, called stragglers, can greatly slow progress. To mitigate the impact of stragglers, we propose an online distributed optimization method called Anytime Minibatch. In this approach, all nodes are given a fixed time to compute the gradients of as many data samples as possible. The result is a variable per-node minibatch size. Workers then get a fixed communication time to average their minibatch gradients via several rounds of consensus, which are then used to update primal variables via dual averaging. Anytime Minibatch prevents stragglers from holding up the system without wasting the work that stragglers can complete. We present a convergence analysis and analyze the wall time performance. Our numerical results show that our approach is up to 1.5 times faster in Amazon EC2 and it is up to five times faster when there is greater variability in compute node performance.

Scaling-up Distributed Processing of Data Streams for Machine Learning

Emerging applications of machine learning in numerous areas involve continuous gathering of and learning from streams of data. Real-time incorporation of streaming data into the learned models is essential for improved inference in these applications. Further, these applications often involve data that are either inherently gathered at geographically distributed entities or that are intentionally distributed across multiple machines for memory, computational, and/or privacy reasons. Training of models in this distributed, streaming setting requires solving stochastic optimization problems in a collaborative manner over communication links between the physical entities. When the streaming data rate is high compared to the processing capabilities of compute nodes and/or the rate of the communications links, this poses a challenging question: how can one best leverage the incoming data for distributed training under constraints on computing capabilities and/or communications rate? A large body of research has emerged in recent decades to tackle this and related problems. This paper reviews recently developed methods that focus on large-scale distributed stochastic optimization in the compute- and bandwidth-limited regime, with an emphasis on convergence analysis that explicitly accounts for the mismatch between computation, communication and streaming rates. In particular, it focuses on methods that solve: (i) distributed stochastic convex problems, and (ii) distributed principal component analysis, which is a nonconvex problem with geometric structure that permits global convergence. For such methods, the paper discusses recent advances in terms of distributed algorithmic designs when faced with high-rate streaming data. Further, it reviews guarantees underlying these methods, which show there exist regimes in which systems can learn from distributed, streaming data at order-optimal rates.

Learning Furniture Compatibility with Graph Neural Networks

We propose a graph neural network (GNN) approach to the problem of predicting the stylistic compatibility of a set of furniture items from images. While most existing results are based on siamese networks which evaluate pairwise compatibility between items, the proposed GNN architecture exploits relational information among groups of items. We present two GNN models, both of which comprise a deep CNN that extracts a feature representation for each image, a gated recurrent unit (GRU) network that models interactions between the furniture items in a set, and an aggregation function that calculates the compatibility score. In the first model, a generalized contrastive loss function that promotes the generation of clustered embeddings for items belonging to the same furniture set is introduced. Also, in the first model, the edge function between nodes in the GRU and the aggregation function are fixed in order to limit model complexity and allow training on smaller datasets; in the second model, the edge function and aggregation function are learned directly from the data. We demonstrate state-of-the art accuracy for compatibility prediction and "fill in the blank" tasks on the Bonn and Singapore furniture datasets. We further introduce a new dataset, called the Target Furniture Collections dataset, which contains over 6000 furniture items that have been hand-curated by stylists to make up 1632 compatible sets. We also demonstrate superior prediction accuracy on this dataset.

An Effective Label Noise Model for DNN Text Classification

Because large, human-annotated datasets suffer from labeling errors, it is crucial to be able to train deep neural networks in the presence of label noise. While training image classification models with label noise have received much attention, training text classification models have not. In this paper, we propose an approach to training deep networks that is robust to label noise. This approach introduces a non-linear processing layer (noise model) that models the statistics of the label noise into a convolutional neural network (CNN) architecture. The noise model and the CNN weights are learned jointly from noisy training data, which prevents the model from overfitting to erroneous labels. Through extensive experiments on several text classification datasets, we show that this approach enables the CNN to learn better sentence representations and is robust even to extreme label noise. We find that proper initialization and regularization of this noise model is critical. Further, by contrast to results focusing on large batch sizes for mitigating label noise for image classification, we find that altering the batch size does not have much effect on classification performance.

Optimizing Taxi Carpool Policies via Reinforcement Learning and Spatio-Temporal Mining

In this paper, we develop a reinforcement learning (RL) based system to learn an effective policy for carpooling that maximizes transportation efficiency so that fewer cars are required to fulfill the given amount of trip demand. For this purpose, first, we develop a deep neural network model, called ST-NN (Spatio-Temporal Neural Network), to predict taxi trip time from the raw GPS trip data. Secondly, we develop a carpooling simulation environment for RL training, with the output of ST-NN and using the NYC taxi trip dataset. In order to maximize transportation efficiency and minimize traffic congestion, we choose the effective distance covered by the driver on a carpool trip as the reward. Therefore, the more effective distance a driver achieves over a trip (i.e. to satisfy more trip demand) the higher the efficiency and the less will be the traffic congestion. We compared the performance of RL learned policy to a fixed policy (which always accepts carpool) as a baseline and obtained promising results that are interpretable and demonstrate the advantage of our RL approach. We also compare the performance of ST-NN to that of state-of-the-art travel time estimation methods and observe that ST-NN significantly improves the prediction performance and is more robust to outliers.

Information Bottleneck Methods for Distributed Learning

We study a distributed learning problem in which Alice sends a compressed distillation of a set of training data to Bob, who uses the distilled version to best solve an associated learning problem. We formalize this as a rate-distortion problem in which the training set is the source and Bob's cross-entropy loss is the distortion measure. We consider this problem for unsupervised learning for batch and sequential data. In the batch data, this problem is equivalent to the information bottleneck (IB), and we show that reduced-complexity versions of standard IB methods solve the associated rate-distortion problem. For the streaming data, we present a new algorithm, which may be of independent interest, that solves the rate-distortion problem for Gaussian sources. Furthermore, to improve the results of the iterative algorithm for sequential data we introduce a two-pass version of this algorithm. Finally, we show the dependency of the rate on the number of samples $k$ required for Gaussian sources to ensure cross-entropy loss that scales optimally with the growth of the training set.

Tensor Matched Kronecker-Structured Subspace Detection for Missing Information

We consider the problem of detecting whether a tensor signal having many missing entities lies within a given low dimensional Kronecker-Structured (KS) subspace. This is a matched subspace detection problem. Tensor matched subspace detection problem is more challenging because of the intertwined signal dimensions. We solve this problem by projecting the signal onto the Kronecker structured subspace, which is a Kronecker product of different subspaces corresponding to each signal dimension. Under this framework, we define the KS subspaces and the orthogonal projection of the signal onto the KS subspace. We prove that reliable detection is possible as long as the cardinality of the missing signal is greater than the dimensions of the KS subspace by bounding the residual energy of the sampling signal with high probability.

Stochastic Optimization from Distributed, Streaming Data in Rate-limited Networks

Motivated by machine learning applications in networks of sensors, internet-of-things (IoT) devices, and autonomous agents, we propose techniques for distributed stochastic convex learning from high-rate data streams. The setup involves a network of nodes---each one of which has a stream of data arriving at a constant rate---that solve a stochastic convex optimization problem by collaborating with each other over rate-limited communication links. To this end, we present and analyze two algorithms---termed distributed stochastic approximation mirror descent (D-SAMD) and accelerated distributed stochastic approximation mirror descent (AD-SAMD)---that are based on two stochastic variants of mirror descent and in which nodes collaborate via approximate averaging of the local, noisy subgradients using distributed consensus. Our main contributions are (i) bounds on the convergence rates of D-SAMD and AD-SAMD in terms of the number of nodes, network topology, and ratio of the data streaming and communication rates, and (ii) sufficient conditions for order-optimum convergence of these algorithms. In particular, we show that for sufficiently well-connected networks, distributed learning schemes can obtain order-optimum convergence even if the communications rate is small. Further we find that the use of accelerated methods significantly enlarges the regime in which order-optimum convergence is achieved; this is in contrast to the centralized setting, where accelerated methods usually offer only a modest improvement. Finally, we demonstrate the effectiveness of the proposed algorithms using numerical experiments.

Classification and Representation via Separable Subspaces: Performance Limits and Algorithms

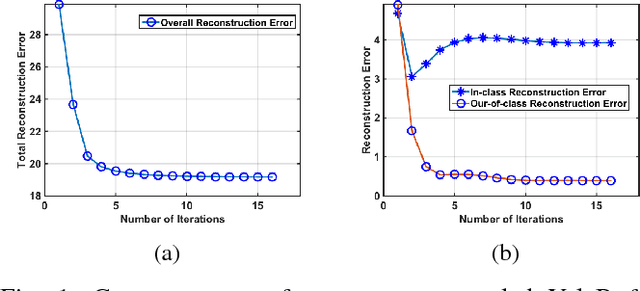
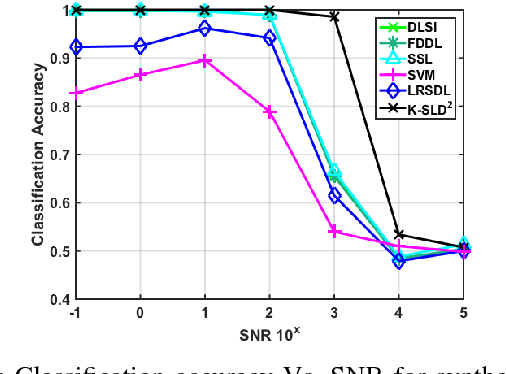
We study the classification performance of Kronecker-structured models in two asymptotic regimes and developed an algorithm for separable, fast and compact K-S dictionary learning for better classification and representation of multidimensional signals by exploiting the structure in the signal. First, we study the classification performance in terms of diversity order and pairwise geometry of the subspaces. We derive an exact expression for the diversity order as a function of the signal and subspace dimensions of a K-S model. Next, we study the classification capacity, the maximum rate at which the number of classes can grow as the signal dimension goes to infinity. Then we describe a fast algorithm for Kronecker-Structured Learning of Discriminative Dictionaries (K-SLD2). Finally, we evaluate the empirical classification performance of K-S models for the synthetic data, showing that they agree with the diversity order analysis. We also evaluate the performance of K-SLD2 on synthetic and real-world datasets showing that the K-SLD2 balances compact signal representation and good classification performance.