Classification and Representation via Separable Subspaces: Performance Limits and Algorithms
Paper and Code
Dec 29, 2017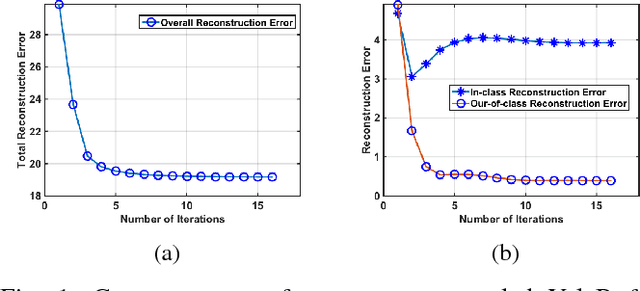

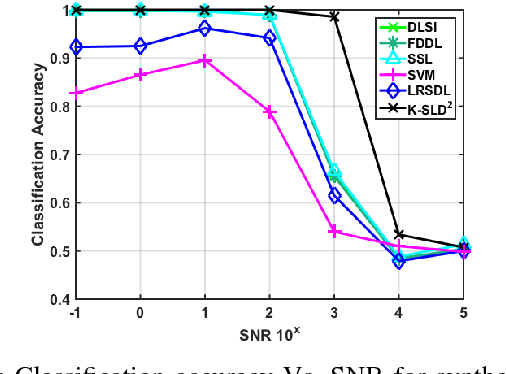

We study the classification performance of Kronecker-structured models in two asymptotic regimes and developed an algorithm for separable, fast and compact K-S dictionary learning for better classification and representation of multidimensional signals by exploiting the structure in the signal. First, we study the classification performance in terms of diversity order and pairwise geometry of the subspaces. We derive an exact expression for the diversity order as a function of the signal and subspace dimensions of a K-S model. Next, we study the classification capacity, the maximum rate at which the number of classes can grow as the signal dimension goes to infinity. Then we describe a fast algorithm for Kronecker-Structured Learning of Discriminative Dictionaries (K-SLD2). Finally, we evaluate the empirical classification performance of K-S models for the synthetic data, showing that they agree with the diversity order analysis. We also evaluate the performance of K-SLD2 on synthetic and real-world datasets showing that the K-SLD2 balances compact signal representation and good classification performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge