Dynamic Subspace Estimation with Grassmannian Geodesics

Dynamic subspace estimation, or subspace tracking, is a fundamental problem in statistical signal processing and machine learning. This paper considers a geodesic model for time-varying subspaces. The natural objective function for this model is non-convex. We propose a novel algorithm for minimizing this objective and estimating the parameters of the model from data with Grassmannian-constrained optimization. We show that with this algorithm, the objective is monotonically non-increasing. We demonstrate the performance of this model and our algorithm on synthetic data, video data, and dynamic fMRI data.

Scaling-up Distributed Processing of Data Streams for Machine Learning

Emerging applications of machine learning in numerous areas involve continuous gathering of and learning from streams of data. Real-time incorporation of streaming data into the learned models is essential for improved inference in these applications. Further, these applications often involve data that are either inherently gathered at geographically distributed entities or that are intentionally distributed across multiple machines for memory, computational, and/or privacy reasons. Training of models in this distributed, streaming setting requires solving stochastic optimization problems in a collaborative manner over communication links between the physical entities. When the streaming data rate is high compared to the processing capabilities of compute nodes and/or the rate of the communications links, this poses a challenging question: how can one best leverage the incoming data for distributed training under constraints on computing capabilities and/or communications rate? A large body of research has emerged in recent decades to tackle this and related problems. This paper reviews recently developed methods that focus on large-scale distributed stochastic optimization in the compute- and bandwidth-limited regime, with an emphasis on convergence analysis that explicitly accounts for the mismatch between computation, communication and streaming rates. In particular, it focuses on methods that solve: (i) distributed stochastic convex problems, and (ii) distributed principal component analysis, which is a nonconvex problem with geometric structure that permits global convergence. For such methods, the paper discusses recent advances in terms of distributed algorithmic designs when faced with high-rate streaming data. Further, it reviews guarantees underlying these methods, which show there exist regimes in which systems can learn from distributed, streaming data at order-optimal rates.

Distributed Stochastic Algorithms for High-rate Streaming Principal Component Analysis

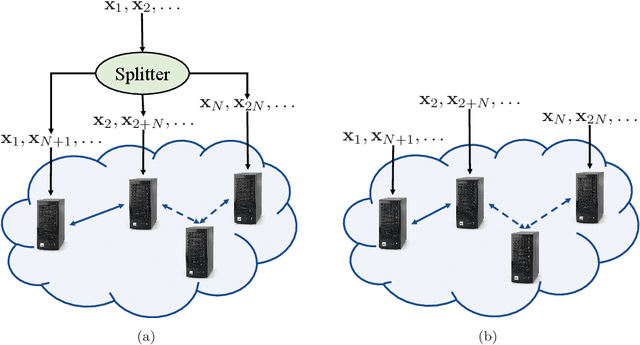
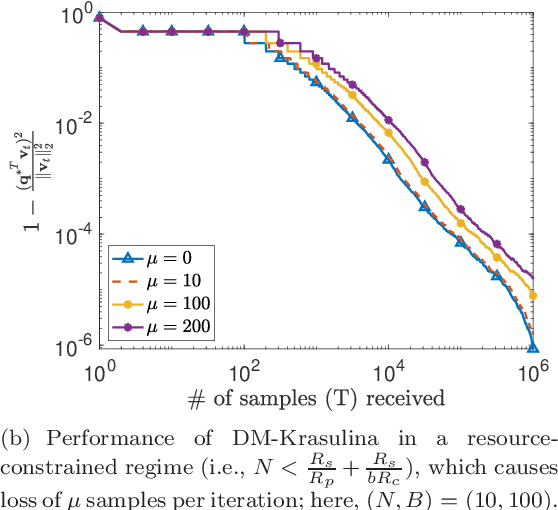
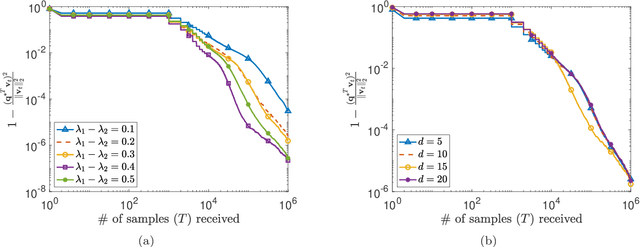
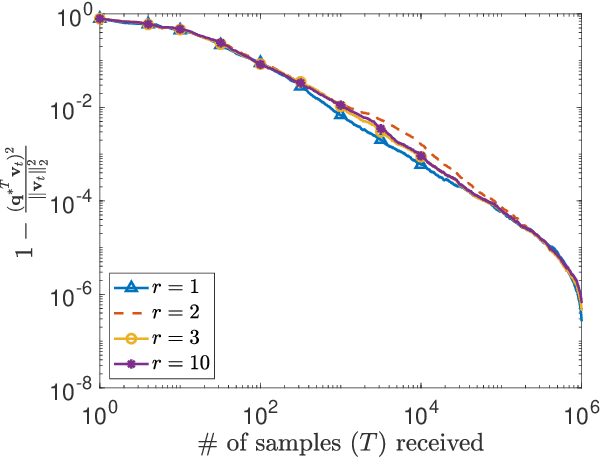
This paper considers the problem of estimating the principal eigenvector of a covariance matrix from independent and identically distributed data samples in streaming settings. The streaming rate of data in many contemporary applications can be high enough that a single processor cannot finish an iteration of existing methods for eigenvector estimation before a new sample arrives. This paper formulates and analyzes a distributed variant of the classical Krasulina's method (D-Krasulina) that can keep up with the high streaming rate of data by distributing the computational load across multiple processing nodes. The analysis shows that---under appropriate conditions---D-Krasulina converges to the principal eigenvector in an order-wise optimal manner; i.e., after receiving $M$ samples across all nodes, its estimation error can be $O(1/M)$. In order to reduce the network communication overhead, the paper also develops and analyzes a mini-batch extension of D-Krasulina, which is termed DM-Krasulina. The analysis of DM-Krasulina shows that it can also achieve order-optimal estimation error rates under appropriate conditions, even when some samples have to be discarded within the network due to communication latency. Finally, experiments are performed over synthetic and real-world data to validate the convergence behaviors of D-Krasulina and DM-Krasulina in high-rate streaming settings.

Tensor Regression Using Low-rank and Sparse Tucker Decompositions

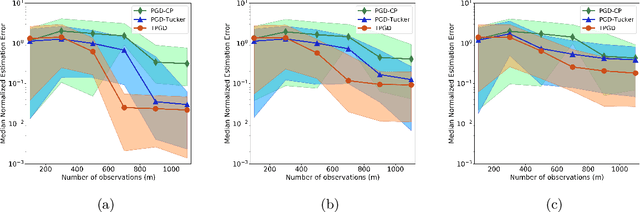
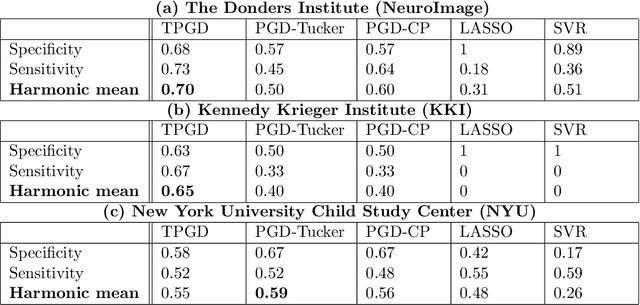
This paper studies a tensor-structured linear regression model with a scalar response variable and tensor-structured predictors, such that the regression parameters form a tensor of order $d$ (i.e., a $d$-fold multiway array) in $\mathbb{R}^{n_1 \times n_2 \times \cdots \times n_d}$. This work focuses on the task of estimating the regression tensor from $m$ realizations of the response variable and the predictors where $m\ll n = \prod \nolimits_{i} n_i$. Despite the ill-posedness of this estimation problem, it can still be solved if the parameter tensor belongs to the space of sparse, low Tucker-rank tensors. Accordingly, the estimation procedure is posed as a non-convex optimization program over the space of sparse, low Tucker-rank tensors, and a tensor variant of projected gradient descent is proposed to solve the resulting non-convex problem. In addition, mathematical guarantees are provided that establish the proposed method converges to the correct solution under the right set of conditions. Further, an upper bound on sample complexity of tensor parameter estimation for the model under consideration is characterized for the special case when the individual (scalar) predictors independently draw values from a sub-Gaussian distribution. The sample complexity bound is shown to have a polylogarithmic dependence on $\bar{n} = \max \big\{n_i: i\in \{1,2,\ldots,d \} \big\}$ and, orderwise, it matches the bound one can obtain from a heuristic parameter counting argument. Finally, numerical experiments demonstrate the efficacy of the proposed tensor model and estimation method on a synthetic dataset and a neuroimaging dataset pertaining to attention deficit hyperactivity disorder. Specifically, the proposed method exhibits better sample complexities on both synthetic and real datasets, demonstrating the usefulness of the model and the method in settings where $n \gg m$.

Cloud K-SVD: A Collaborative Dictionary Learning Algorithm for Big, Distributed Data

This paper studies the problem of data-adaptive representations for big, distributed data. It is assumed that a number of geographically-distributed, interconnected sites have massive local data and they are interested in collaboratively learning a low-dimensional geometric structure underlying these data. In contrast to previous works on subspace-based data representations, this paper focuses on the geometric structure of a union of subspaces (UoS). In this regard, it proposes a distributed algorithm---termed cloud K-SVD---for collaborative learning of a UoS structure underlying distributed data of interest. The goal of cloud K-SVD is to learn a common overcomplete dictionary at each individual site such that every sample in the distributed data can be represented through a small number of atoms of the learned dictionary. Cloud K-SVD accomplishes this goal without requiring exchange of individual samples between sites. This makes it suitable for applications where sharing of raw data is discouraged due to either privacy concerns or large volumes of data. This paper also provides an analysis of cloud K-SVD that gives insights into its properties as well as deviations of the dictionaries learned at individual sites from a centralized solution in terms of different measures of local/global data and topology of interconnections. Finally, the paper numerically illustrates the efficacy of cloud K-SVD on real and synthetic distributed data.