Tensor Regression Using Low-rank and Sparse Tucker Decompositions

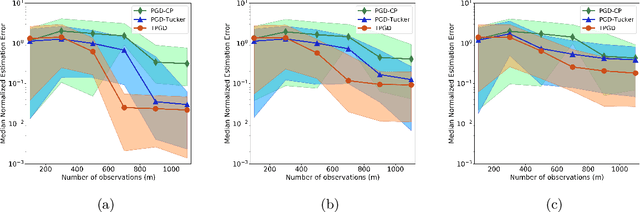
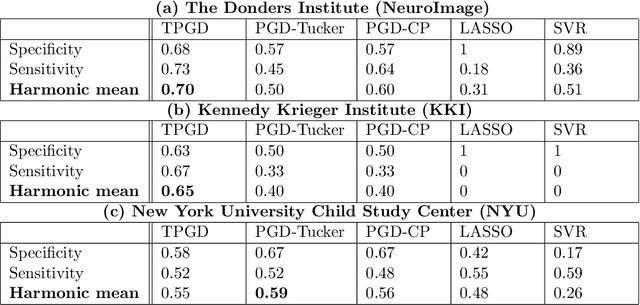
This paper studies a tensor-structured linear regression model with a scalar response variable and tensor-structured predictors, such that the regression parameters form a tensor of order $d$ (i.e., a $d$-fold multiway array) in $\mathbb{R}^{n_1 \times n_2 \times \cdots \times n_d}$. This work focuses on the task of estimating the regression tensor from $m$ realizations of the response variable and the predictors where $m\ll n = \prod \nolimits_{i} n_i$. Despite the ill-posedness of this estimation problem, it can still be solved if the parameter tensor belongs to the space of sparse, low Tucker-rank tensors. Accordingly, the estimation procedure is posed as a non-convex optimization program over the space of sparse, low Tucker-rank tensors, and a tensor variant of projected gradient descent is proposed to solve the resulting non-convex problem. In addition, mathematical guarantees are provided that establish the proposed method converges to the correct solution under the right set of conditions. Further, an upper bound on sample complexity of tensor parameter estimation for the model under consideration is characterized for the special case when the individual (scalar) predictors independently draw values from a sub-Gaussian distribution. The sample complexity bound is shown to have a polylogarithmic dependence on $\bar{n} = \max \big\{n_i: i\in \{1,2,\ldots,d \} \big\}$ and, orderwise, it matches the bound one can obtain from a heuristic parameter counting argument. Finally, numerical experiments demonstrate the efficacy of the proposed tensor model and estimation method on a synthetic dataset and a neuroimaging dataset pertaining to attention deficit hyperactivity disorder. Specifically, the proposed method exhibits better sample complexities on both synthetic and real datasets, demonstrating the usefulness of the model and the method in settings where $n \gg m$.