Talal Ahmed
Tensor Regression Using Low-rank and Sparse Tucker Decompositions
Nov 09, 2019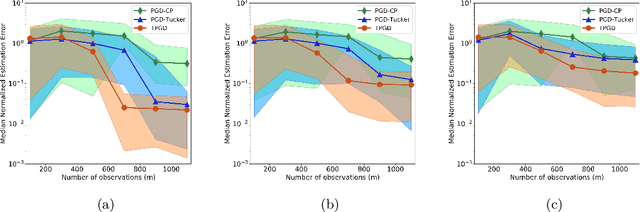
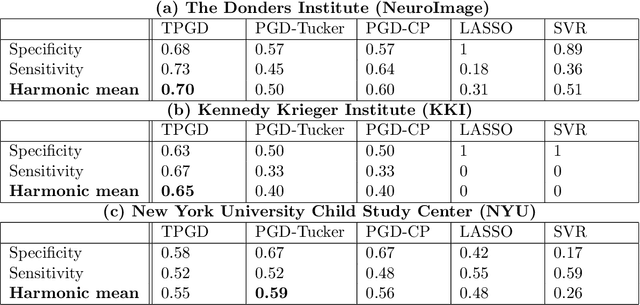
Abstract:This paper studies a tensor-structured linear regression model with a scalar response variable and tensor-structured predictors, such that the regression parameters form a tensor of order $d$ (i.e., a $d$-fold multiway array) in $\mathbb{R}^{n_1 \times n_2 \times \cdots \times n_d}$. This work focuses on the task of estimating the regression tensor from $m$ realizations of the response variable and the predictors where $m\ll n = \prod \nolimits_{i} n_i$. Despite the ill-posedness of this estimation problem, it can still be solved if the parameter tensor belongs to the space of sparse, low Tucker-rank tensors. Accordingly, the estimation procedure is posed as a non-convex optimization program over the space of sparse, low Tucker-rank tensors, and a tensor variant of projected gradient descent is proposed to solve the resulting non-convex problem. In addition, mathematical guarantees are provided that establish the proposed method converges to the correct solution under the right set of conditions. Further, an upper bound on sample complexity of tensor parameter estimation for the model under consideration is characterized for the special case when the individual (scalar) predictors independently draw values from a sub-Gaussian distribution. The sample complexity bound is shown to have a polylogarithmic dependence on $\bar{n} = \max \big\{n_i: i\in \{1,2,\ldots,d \} \big\}$ and, orderwise, it matches the bound one can obtain from a heuristic parameter counting argument. Finally, numerical experiments demonstrate the efficacy of the proposed tensor model and estimation method on a synthetic dataset and a neuroimaging dataset pertaining to attention deficit hyperactivity disorder. Specifically, the proposed method exhibits better sample complexities on both synthetic and real datasets, demonstrating the usefulness of the model and the method in settings where $n \gg m$.
ExSIS: Extended Sure Independence Screening for Ultrahigh-dimensional Linear Models
Aug 21, 2017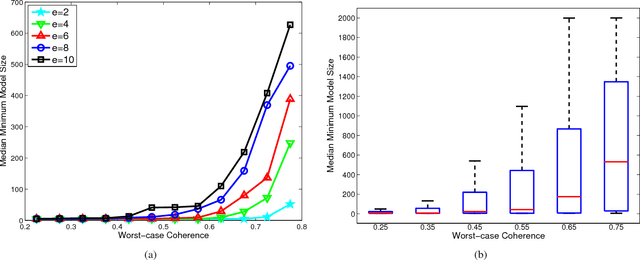
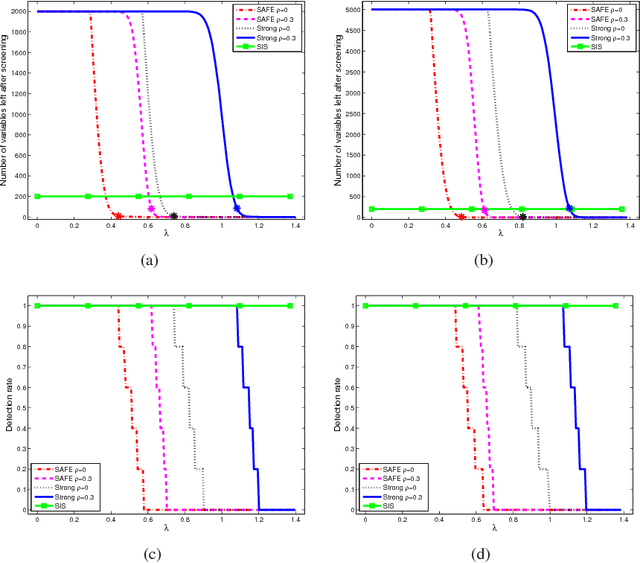
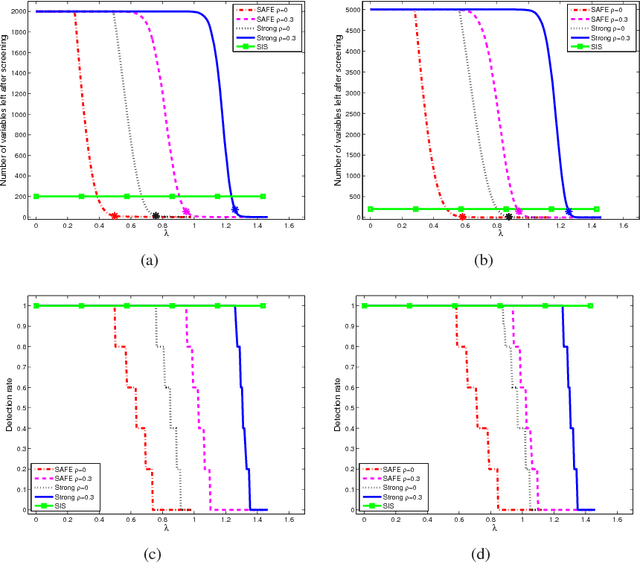

Abstract:Statistical inference can be computationally prohibitive in ultrahigh-dimensional linear models. Correlation-based variable screening, in which one leverages marginal correlations for removal of irrelevant variables from the model prior to statistical inference, can be used to overcome this challenge. Prior works on correlation-based variable screening either impose strong statistical priors on the linear model or assume specific post-screening inference methods. This paper first extends the analysis of correlation-based variable screening to arbitrary linear models and post-screening inference techniques. In particular, ($i$) it shows that a condition---termed the screening condition---is sufficient for successful correlation-based screening of linear models, and ($ii$) it provides insights into the dependence of marginal correlation-based screening on different problem parameters. Numerical experiments confirm that these insights are not mere artifacts of analysis; rather, they are reflective of the challenges associated with marginal correlation-based variable screening. Second, the paper explicitly derives the screening condition for two families of linear models, namely, sub-Gaussian linear models and arbitrary (random or deterministic) linear models. In the process, it establishes that---under appropriate conditions---it is possible to reduce the dimension of an ultrahigh-dimensional, arbitrary linear model to almost the sample size even when the number of active variables scales almost linearly with the sample size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge