ExSIS: Extended Sure Independence Screening for Ultrahigh-dimensional Linear Models

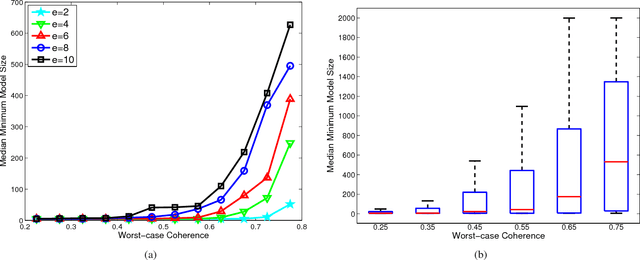
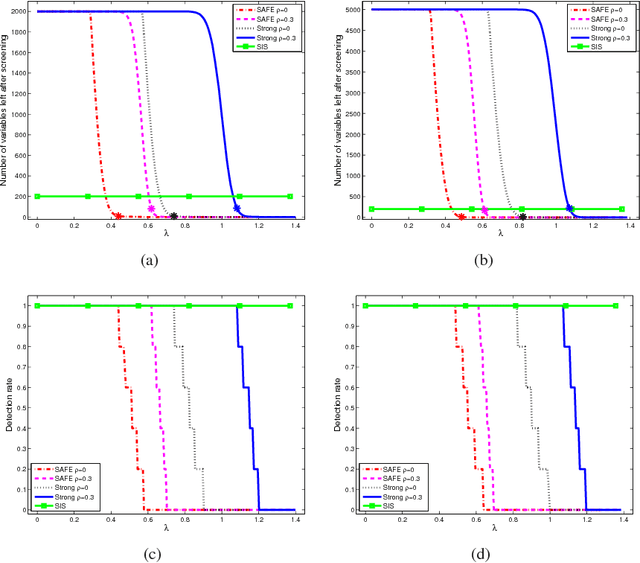
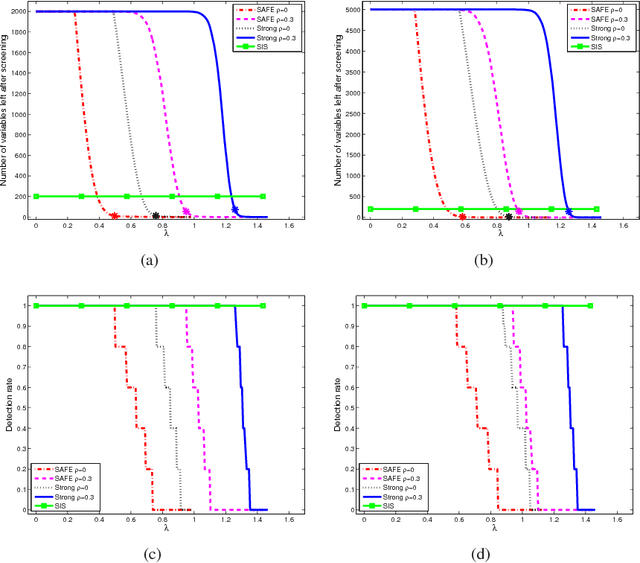
Statistical inference can be computationally prohibitive in ultrahigh-dimensional linear models. Correlation-based variable screening, in which one leverages marginal correlations for removal of irrelevant variables from the model prior to statistical inference, can be used to overcome this challenge. Prior works on correlation-based variable screening either impose strong statistical priors on the linear model or assume specific post-screening inference methods. This paper first extends the analysis of correlation-based variable screening to arbitrary linear models and post-screening inference techniques. In particular, ($i$) it shows that a condition---termed the screening condition---is sufficient for successful correlation-based screening of linear models, and ($ii$) it provides insights into the dependence of marginal correlation-based screening on different problem parameters. Numerical experiments confirm that these insights are not mere artifacts of analysis; rather, they are reflective of the challenges associated with marginal correlation-based variable screening. Second, the paper explicitly derives the screening condition for two families of linear models, namely, sub-Gaussian linear models and arbitrary (random or deterministic) linear models. In the process, it establishes that---under appropriate conditions---it is possible to reduce the dimension of an ultrahigh-dimensional, arbitrary linear model to almost the sample size even when the number of active variables scales almost linearly with the sample size.