Structure Learning in Gaussian Graphical Models from Glauber Dynamics

Gaussian graphical model selection is an important paradigm with numerous applications, including biological network modeling, financial network modeling, and social network analysis. Traditional approaches assume access to independent and identically distributed (i.i.d) samples, which is often impractical in real-world scenarios. In this paper, we address Gaussian graphical model selection under observations from a more realistic dependent stochastic process known as Glauber dynamics. Glauber dynamics, also called the Gibbs sampler, is a Markov chain that sequentially updates the variables of the underlying model based on the statistics of the remaining model. Such models, aside from frequently being employed to generate samples from complex multivariate distributions, naturally arise in various settings, such as opinion consensus in social networks and clearing/stock-price dynamics in financial networks. In contrast to the extensive body of existing work, we present the first algorithm for Gaussian graphical model selection when data are sampled according to the Glauber dynamics. We provide theoretical guarantees on the computational and statistical complexity of the proposed algorithm's structure learning performance. Additionally, we provide information-theoretic lower bounds on the statistical complexity and show that our algorithm is nearly minimax optimal for a broad class of problems.

Learning Networks from Wide-Sense Stationary Stochastic Processes

Complex networked systems driven by latent inputs are common in fields like neuroscience, finance, and engineering. A key inference problem here is to learn edge connectivity from node outputs (potentials). We focus on systems governed by steady-state linear conservation laws: $X_t = {L^{\ast}}Y_{t}$, where $X_t, Y_t \in \mathbb{R}^p$ denote inputs and potentials, respectively, and the sparsity pattern of the $p \times p$ Laplacian $L^{\ast}$ encodes the edge structure. Assuming $X_t$ to be a wide-sense stationary stochastic process with a known spectral density matrix, we learn the support of $L^{\ast}$ from temporally correlated samples of $Y_t$ via an $\ell_1$-regularized Whittle's maximum likelihood estimator (MLE). The regularization is particularly useful for learning large-scale networks in the high-dimensional setting where the network size $p$ significantly exceeds the number of samples $n$. We show that the MLE problem is strictly convex, admitting a unique solution. Under a novel mutual incoherence condition and certain sufficient conditions on $(n, p, d)$, we show that the ML estimate recovers the sparsity pattern of $L^\ast$ with high probability, where $d$ is the maximum degree of the graph underlying $L^{\ast}$. We provide recovery guarantees for $L^\ast$ in element-wise maximum, Frobenius, and operator norms. Finally, we complement our theoretical results with several simulation studies on synthetic and benchmark datasets, including engineered systems (power and water networks), and real-world datasets from neural systems (such as the human brain).

Learning the Structure of Large Networked Systems Obeying Conservation Laws

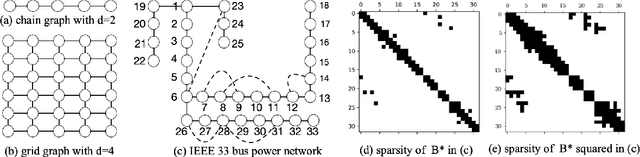
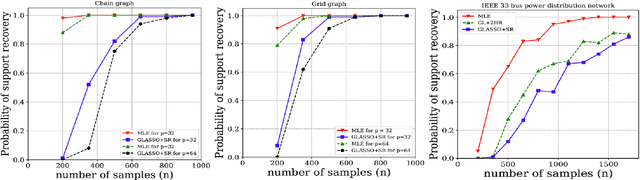
Many networked systems such as electric networks, the brain, and social networks of opinion dynamics are known to obey conservation laws. Examples of this phenomenon include the Kirchoff laws in electric networks and opinion consensus in social networks. Conservation laws in networked systems may be modeled as balance equations of the form $X = B^{*} Y$, where the sparsity pattern of $B^{*}$ captures the connectivity of the network, and $Y, X \in \mathbb{R}^p$ are vectors of "potentials" and "injected flows" at the nodes respectively. The node potentials $Y$ cause flows across edges and the flows $X$ injected at the nodes are extraneous to the network dynamics. In several practical systems, the network structure is often unknown and needs to be estimated from data. Towards this, one has access to samples of the node potentials $Y$, but only the statistics of the node injections $X$. Motivated by this important problem, we study the estimation of the sparsity structure of the matrix $B^{*}$ from $n$ samples of $Y$ under the assumption that the node injections $X$ follow a Gaussian distribution with a known covariance $\Sigma_X$. We propose a new $\ell_{1}$-regularized maximum likelihood estimator for this problem in the high-dimensional regime where the size of the network $p$ is larger than sample size $n$. We show that this optimization problem is convex in the objective and admits a unique solution. Under a new mutual incoherence condition, we establish sufficient conditions on the triple $(n,p,d)$ for which exact sparsity recovery of $B^{*}$ is possible with high probability; $d$ is the degree of the graph. We also establish guarantees for the recovery of $B^{*}$ in the element-wise maximum, Frobenius, and operator norms. Finally, we complement these theoretical results with experimental validation of the performance of the proposed estimator on synthetic and real-world data.