Taming Adversarial Robustness via Abstaining

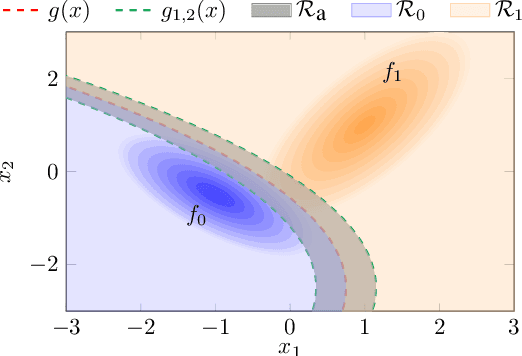
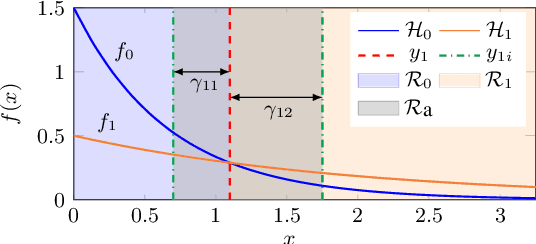
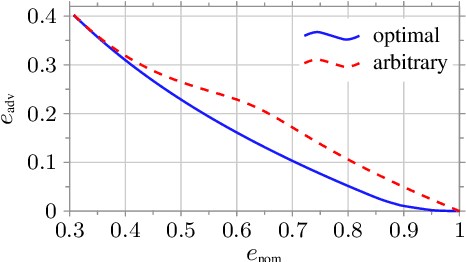
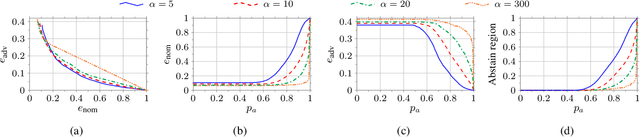
In this work, we consider a binary classification problem and cast it into a binary hypothesis testing framework, where the observations can be perturbed by an adversary. To improve the adversarial robustness of a classifier, we include an abstaining option, where the classifier abstains from taking a decision when it has low confidence about the prediction. We propose metrics to quantify the nominal performance of a classifier with abstaining option and its robustness against adversarial perturbations. We show that there exist a tradeoff between the two metrics regardless of what method is used to choose the abstaining region. Our results imply that the robustness of a classifier with abstaining can only be improved at the expense of its nominal performance. Further, we provide necessary conditions to design the abstaining region for a 1-dimensional binary classification problem. We validate our theoretical results on the MNIST dataset, where we numerically show that the tradeoff between performance and robustness also exist for the general multi-class classification problems.

Learning Robust Feedback Policies from Demonstrations

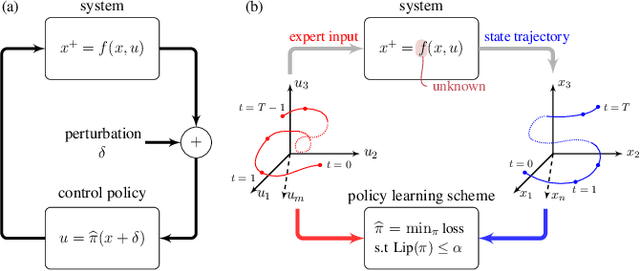
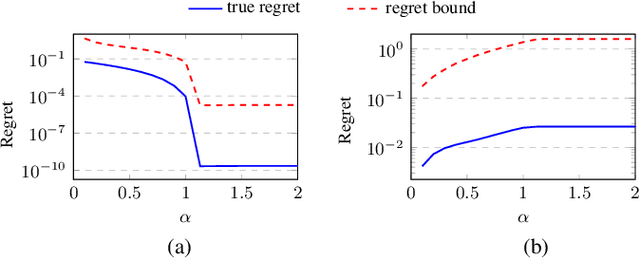
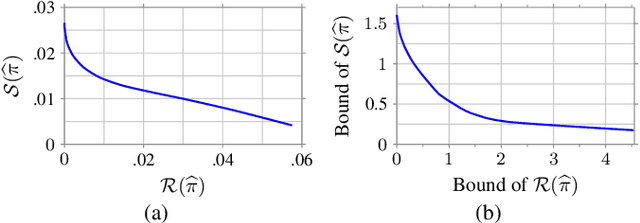
In this work we propose and analyze a new framework to learn feedback control policies that exhibit provable guarantees on the closed-loop performance and robustness to bounded (adversarial) perturbations. These policies are learned from expert demonstrations without any prior knowledge of the task, its cost function, and system dynamics. In contrast to the existing algorithms in imitation learning and inverse reinforcement learning, we use a Lipschitz-constrained loss minimization scheme to learn control policies with certified robustness. We establish robust stability of the closed-loop system under the learned control policy and derive an upper bound on its regret, which bounds the sub-optimality of the closed-loop performance with respect to the expert policy. We also derive a robustness bound for the deterioration of the closed-loop performance under bounded (adversarial) perturbations on the state measurements. Ultimately, our results suggest the existence of an underlying tradeoff between nominal closed-loop performance and adversarial robustness, and that improvements in nominal closed-loop performance can only be made at the expense of robustness to adversarial perturbations. Numerical results validate our analysis and demonstrate the effectiveness of our robust feedback policy learning framework.

Lipschitz Bounds and Provably Robust Training by Laplacian Smoothing

In this work we propose a graph-based learning framework to train models with provable robustness to adversarial perturbations. In contrast to regularization-based approaches, we formulate the adversarially robust learning problem as one of loss minimization with a Lipschitz constraint, and show that the saddle point of the associated Lagrangian is characterized by a Poisson equation with weighted Laplace operator. Further, the weighting for the Laplace operator is given by the Lagrange multiplier for the Lipschitz constraint, which modulates the sensitivity of the minimizer to perturbations. We then design a provably robust training scheme using graph-based discretization of the input space and a primal-dual algorithm to converge to the Lagrangian's saddle point. Our analysis establishes a novel connection between elliptic operators with constraint-enforced weighting and adversarial learning. We also study the complementary problem of improving the robustness of minimizers with a margin on their loss, formulated as a loss-constrained minimization problem of the Lipschitz constant. We propose a technique to obtain robustified minimizers, and evaluate fundamental Lipschitz lower bounds by approaching Lipschitz constant minimization via a sequence of gradient $p$-norm minimization problems. Ultimately, our results show that, for a desired nominal performance, there exists a fundamental lower bound on the sensitivity to adversarial perturbations that depends only on the loss function and the data distribution, and that improvements in robustness beyond this bound can only be made at the expense of nominal performance. Our training schemes provably achieve these bounds both under constraints on performance and~robustness.

On the Robustness of Data-Driven Controllers for Linear Systems

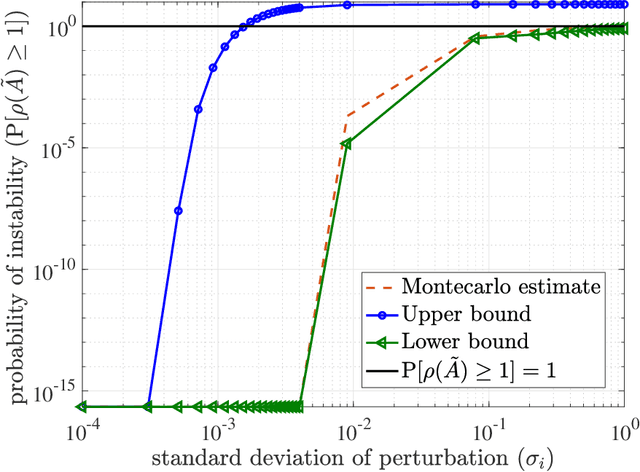
This paper proposes a new framework and several results to quantify the performance of data-driven state-feedback controllers for linear systems against targeted perturbations of the training data. We focus on the case where subsets of the training data are randomly corrupted by an adversary, and derive lower and upper bounds for the stability of the closed-loop system with compromised controller as a function of the perturbation statistics, size of the training data, sensitivity of the data-driven algorithm to perturbation of the training data, and properties of the nominal closed-loop system. Our stability and convergence bounds are probabilistic in nature, and rely on a first-order approximation of the data-driven procedure that designs the state-feedback controller, which can be computed directly using the training data. We illustrate our findings via multiple numerical studies.

A Fundamental Performance Limitation for Adversarial Classification

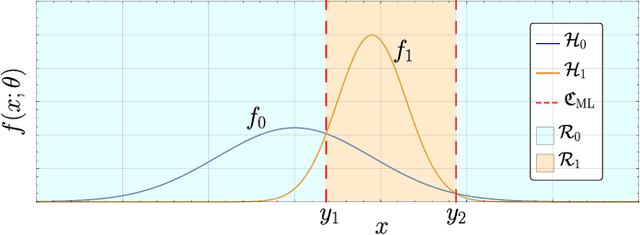
Despite the widespread use of machine learning algorithms to solve problems of technological, economic, and social relevance, provable guarantees on the performance of these data-driven algorithms are critically lacking, especially when the data originates from unreliable sources and is transmitted over unprotected and easily accessible channels. In this paper we take an important step to bridge this gap and formally show that, in a quest to optimize their accuracy, binary classification algorithms -- including those based on machine-learning techniques -- inevitably become more sensitive to adversarial manipulation of the data. Further, for a given class of algorithms with the same complexity (i.e., number of classification boundaries), the fundamental tradeoff curve between accuracy and sensitivity depends solely on the statistics of the data, and cannot be improved by tuning the algorithm.