Taming Adversarial Robustness via Abstaining
Paper and Code
Apr 06, 2021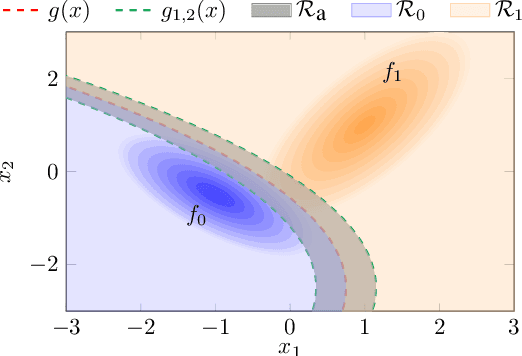
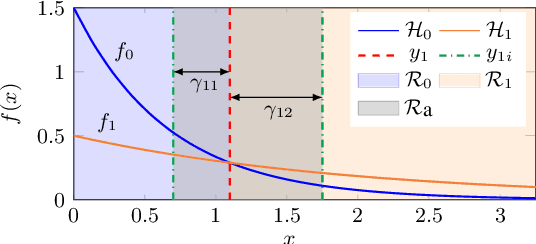
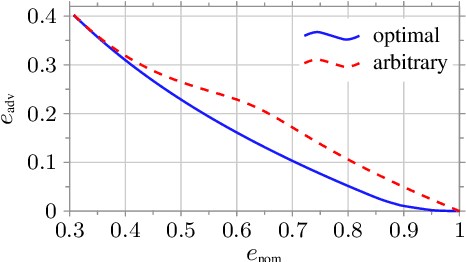
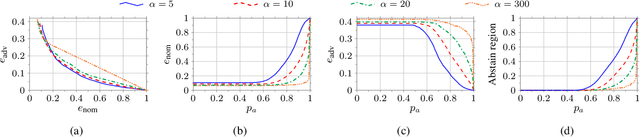
In this work, we consider a binary classification problem and cast it into a binary hypothesis testing framework, where the observations can be perturbed by an adversary. To improve the adversarial robustness of a classifier, we include an abstaining option, where the classifier abstains from taking a decision when it has low confidence about the prediction. We propose metrics to quantify the nominal performance of a classifier with abstaining option and its robustness against adversarial perturbations. We show that there exist a tradeoff between the two metrics regardless of what method is used to choose the abstaining region. Our results imply that the robustness of a classifier with abstaining can only be improved at the expense of its nominal performance. Further, we provide necessary conditions to design the abstaining region for a 1-dimensional binary classification problem. We validate our theoretical results on the MNIST dataset, where we numerically show that the tradeoff between performance and robustness also exist for the general multi-class classification problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge