Exploiting Adjacent Similarity in Multi-Armed Bandit Tasks via Transfer of Reward Samples

We consider a sequential multi-task problem, where each task is modeled as the stochastic multi-armed bandit with K arms. We assume the bandit tasks are adjacently similar in the sense that the difference between the mean rewards of the arms for any two consecutive tasks is bounded by a parameter. We propose two algorithms (one assumes the parameter is known while the other does not) based on UCB to transfer reward samples from preceding tasks to improve the overall regret across all tasks. Our analysis shows that transferring samples reduces the regret as compared to the case of no transfer. We provide empirical results for our algorithms, which show performance improvement over the standard UCB algorithm without transfer and a naive transfer algorithm.

Transfer in Sequential Multi-armed Bandits via Reward Samples

We consider a sequential stochastic multi-armed bandit problem where the agent interacts with bandit over multiple episodes. The reward distribution of the arms remain constant throughout an episode but can change over different episodes. We propose an algorithm based on UCB to transfer the reward samples from the previous episodes and improve the cumulative regret performance over all the episodes. We provide regret analysis and empirical results for our algorithm, which show significant improvement over the standard UCB algorithm without transfer.

Control Barrier Functions in UGVs for Kinematic Obstacle Avoidance: A Collision Cone Approach

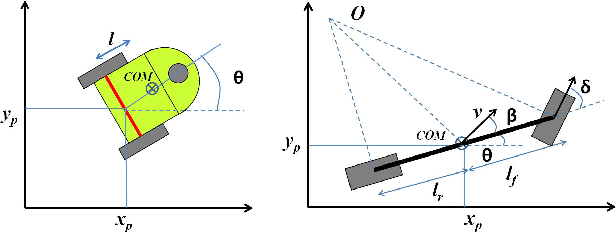
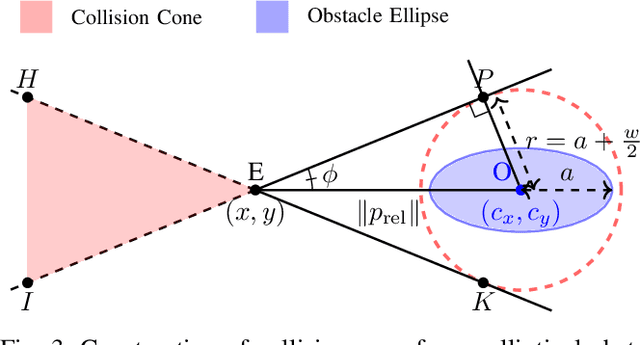
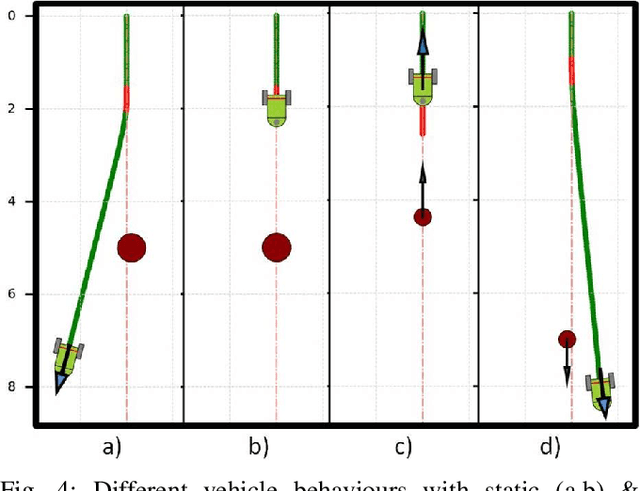
In this paper, we propose a new class of Control Barrier Functions (CBFs) for Unmanned Ground Vehicles (UGVs) that help avoid collisions with kinematic (non-zero velocity) obstacles. While the current forms of CBFs have been successful in guaranteeing safety/collision avoidance with static obstacles, extensions for the dynamic case have seen limited success. Moreover, with the UGV models like the unicycle or the bicycle, applications of existing CBFs have been conservative in terms of control, i.e., steering/thrust control has not been possible under certain scenarios. Drawing inspiration from the classical use of collision cones for obstacle avoidance in trajectory planning, we introduce its novel CBF formulation with theoretical guarantees on safety for both the unicycle and bicycle models. The main idea is to ensure that the velocity of the obstacle w.r.t. the vehicle is always pointing away from the vehicle. Accordingly, we construct a constraint that ensures that the velocity vector always avoids a cone of vectors pointing at the vehicle. The efficacy of this new control methodology is experimentally verified on the Copernicus mobile robot. We further extend it to self-driving cars in the form of bicycle models and demonstrate collision avoidance under various scenarios in the CARLA simulator.

Taming Adversarial Robustness via Abstaining

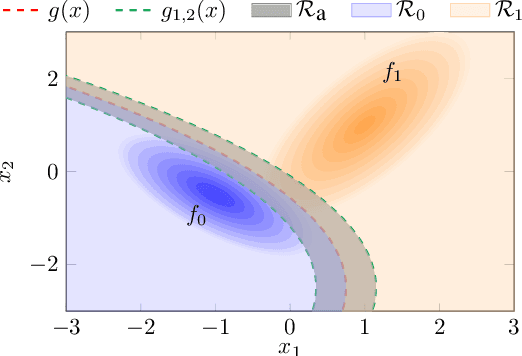
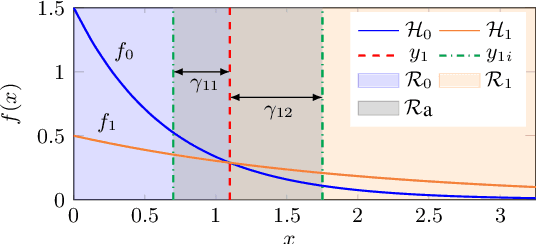
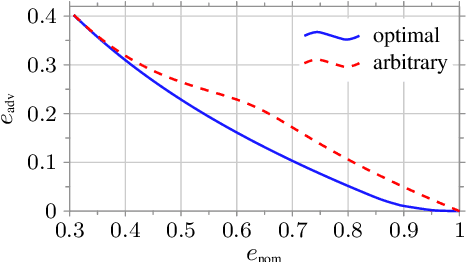
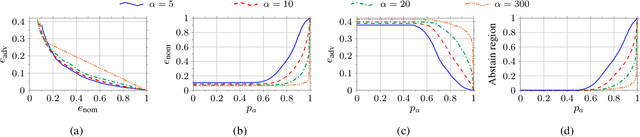
In this work, we consider a binary classification problem and cast it into a binary hypothesis testing framework, where the observations can be perturbed by an adversary. To improve the adversarial robustness of a classifier, we include an abstaining option, where the classifier abstains from taking a decision when it has low confidence about the prediction. We propose metrics to quantify the nominal performance of a classifier with abstaining option and its robustness against adversarial perturbations. We show that there exist a tradeoff between the two metrics regardless of what method is used to choose the abstaining region. Our results imply that the robustness of a classifier with abstaining can only be improved at the expense of its nominal performance. Further, we provide necessary conditions to design the abstaining region for a 1-dimensional binary classification problem. We validate our theoretical results on the MNIST dataset, where we numerically show that the tradeoff between performance and robustness also exist for the general multi-class classification problems.

On the Robustness of Data-Driven Controllers for Linear Systems

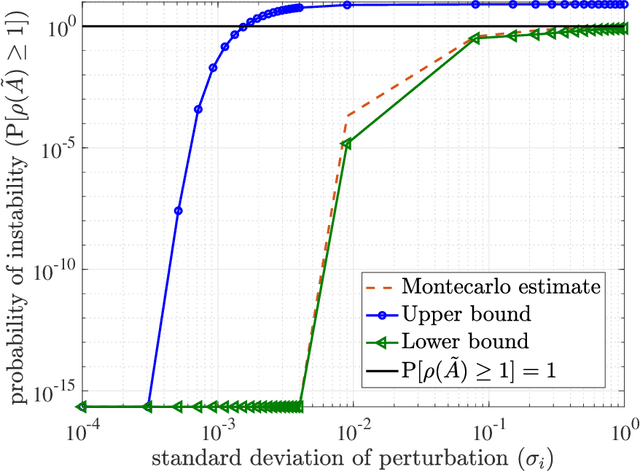
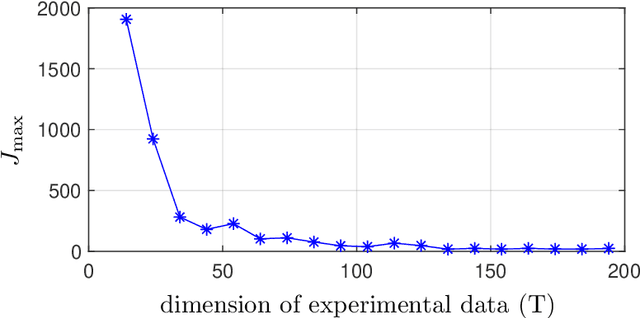
This paper proposes a new framework and several results to quantify the performance of data-driven state-feedback controllers for linear systems against targeted perturbations of the training data. We focus on the case where subsets of the training data are randomly corrupted by an adversary, and derive lower and upper bounds for the stability of the closed-loop system with compromised controller as a function of the perturbation statistics, size of the training data, sensitivity of the data-driven algorithm to perturbation of the training data, and properties of the nominal closed-loop system. Our stability and convergence bounds are probabilistic in nature, and rely on a first-order approximation of the data-driven procedure that designs the state-feedback controller, which can be computed directly using the training data. We illustrate our findings via multiple numerical studies.

A Fundamental Performance Limitation for Adversarial Classification

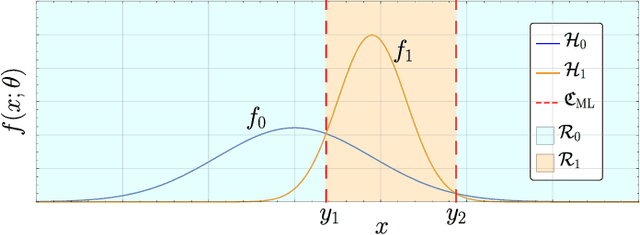
Despite the widespread use of machine learning algorithms to solve problems of technological, economic, and social relevance, provable guarantees on the performance of these data-driven algorithms are critically lacking, especially when the data originates from unreliable sources and is transmitted over unprotected and easily accessible channels. In this paper we take an important step to bridge this gap and formally show that, in a quest to optimize their accuracy, binary classification algorithms -- including those based on machine-learning techniques -- inevitably become more sensitive to adversarial manipulation of the data. Further, for a given class of algorithms with the same complexity (i.e., number of classification boundaries), the fundamental tradeoff curve between accuracy and sensitivity depends solely on the statistics of the data, and cannot be improved by tuning the algorithm.