Hamiltonian bridge: A physics-driven generative framework for targeted pattern control

Patterns arise spontaneously in a range of systems spanning the sciences, and their study typically focuses on mechanisms to understand their evolution in space-time. Increasingly, there has been a transition towards controlling these patterns in various functional settings, with implications for engineering. Here, we combine our knowledge of a general class of dynamical laws for pattern formation in non-equilibrium systems, and the power of stochastic optimal control approaches to present a framework that allows us to control patterns at multiple scales, which we dub the "Hamiltonian bridge". We use a mapping between stochastic many-body Lagrangian physics and deterministic Eulerian pattern forming PDEs to leverage our recent approach utilizing the Feynman-Kac-based adjoint path integral formulation for the control of interacting particles and generalize this to the active control of patterning fields. We demonstrate the applicability of our computational framework via numerical experiments on the control of phase separation with and without a conserved order parameter, self-assembly of fluid droplets, coupled reaction-diffusion equations and finally a phenomenological model for spatio-temporal tissue differentiation. We interpret our numerical experiments in terms of a theoretical understanding of how the underlying physics shapes the geometry of the pattern manifold, altering the transport paths of patterns and the nature of pattern interpolation. We finally conclude by showing how optimal control can be utilized to generate complex patterns via an iterative control protocol over pattern forming pdes which can be casted as gradient flows. All together, our study shows how we can systematically build in physical priors into a generative framework for pattern control in non-equilibrium systems across multiple length and time scales.

Learning Robust Feedback Policies from Demonstrations

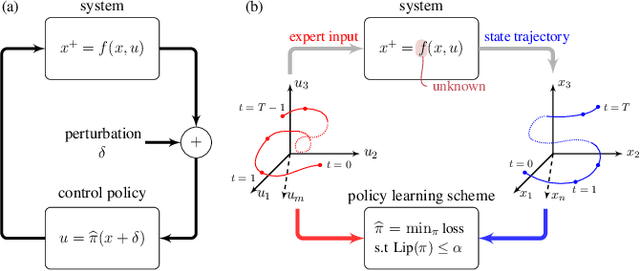
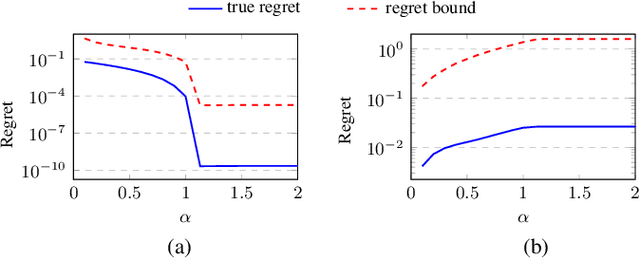
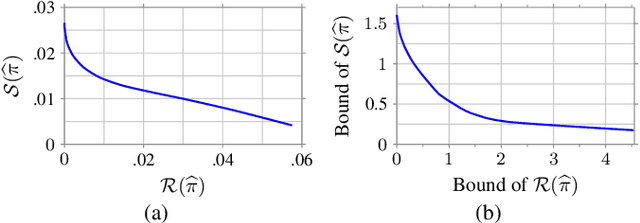
In this work we propose and analyze a new framework to learn feedback control policies that exhibit provable guarantees on the closed-loop performance and robustness to bounded (adversarial) perturbations. These policies are learned from expert demonstrations without any prior knowledge of the task, its cost function, and system dynamics. In contrast to the existing algorithms in imitation learning and inverse reinforcement learning, we use a Lipschitz-constrained loss minimization scheme to learn control policies with certified robustness. We establish robust stability of the closed-loop system under the learned control policy and derive an upper bound on its regret, which bounds the sub-optimality of the closed-loop performance with respect to the expert policy. We also derive a robustness bound for the deterioration of the closed-loop performance under bounded (adversarial) perturbations on the state measurements. Ultimately, our results suggest the existence of an underlying tradeoff between nominal closed-loop performance and adversarial robustness, and that improvements in nominal closed-loop performance can only be made at the expense of robustness to adversarial perturbations. Numerical results validate our analysis and demonstrate the effectiveness of our robust feedback policy learning framework.

Lipschitz Bounds and Provably Robust Training by Laplacian Smoothing

In this work we propose a graph-based learning framework to train models with provable robustness to adversarial perturbations. In contrast to regularization-based approaches, we formulate the adversarially robust learning problem as one of loss minimization with a Lipschitz constraint, and show that the saddle point of the associated Lagrangian is characterized by a Poisson equation with weighted Laplace operator. Further, the weighting for the Laplace operator is given by the Lagrange multiplier for the Lipschitz constraint, which modulates the sensitivity of the minimizer to perturbations. We then design a provably robust training scheme using graph-based discretization of the input space and a primal-dual algorithm to converge to the Lagrangian's saddle point. Our analysis establishes a novel connection between elliptic operators with constraint-enforced weighting and adversarial learning. We also study the complementary problem of improving the robustness of minimizers with a margin on their loss, formulated as a loss-constrained minimization problem of the Lipschitz constant. We propose a technique to obtain robustified minimizers, and evaluate fundamental Lipschitz lower bounds by approaching Lipschitz constant minimization via a sequence of gradient $p$-norm minimization problems. Ultimately, our results show that, for a desired nominal performance, there exists a fundamental lower bound on the sensitivity to adversarial perturbations that depends only on the loss function and the data distribution, and that improvements in robustness beyond this bound can only be made at the expense of nominal performance. Our training schemes provably achieve these bounds both under constraints on performance and~robustness.