Emergent functional dynamics of link-bots

Synthetic active collectives, composed of many nonliving individuals capable of cooperative changes in group shape and dynamics, hold promise for practical applications and for the elucidation of guiding principles of natural collectives. However, the design of collective robotic systems that operate effectively without intelligence or complex control at either the individual or group level is challenging. We investigate how simple steric interaction constraints between active individuals produce a versatile active system with promising functionality. Here we introduce the link-bot: a V-shape-based, single-stranded chain composed of active bots whose dynamics are defined by its geometric link constraints, allowing it to possess scale- and processing-free programmable collective behaviors. A variety of emergent properties arise from this dynamic system, including locomotion, navigation, transportation, and competitive or cooperative interactions. Through the control of a few link parameters, link-bots show rich usefulness by performing a variety of divergent tasks, including traversing or obstructing narrow spaces, passing by or enclosing objects, and propelling loads in both forward and backward directions. The reconfigurable nature of the link-bot suggests that our approach may significantly contribute to the development of programmable soft robotic systems with minimal information and materials at any scale.

Hamiltonian bridge: A physics-driven generative framework for targeted pattern control

Patterns arise spontaneously in a range of systems spanning the sciences, and their study typically focuses on mechanisms to understand their evolution in space-time. Increasingly, there has been a transition towards controlling these patterns in various functional settings, with implications for engineering. Here, we combine our knowledge of a general class of dynamical laws for pattern formation in non-equilibrium systems, and the power of stochastic optimal control approaches to present a framework that allows us to control patterns at multiple scales, which we dub the "Hamiltonian bridge". We use a mapping between stochastic many-body Lagrangian physics and deterministic Eulerian pattern forming PDEs to leverage our recent approach utilizing the Feynman-Kac-based adjoint path integral formulation for the control of interacting particles and generalize this to the active control of patterning fields. We demonstrate the applicability of our computational framework via numerical experiments on the control of phase separation with and without a conserved order parameter, self-assembly of fluid droplets, coupled reaction-diffusion equations and finally a phenomenological model for spatio-temporal tissue differentiation. We interpret our numerical experiments in terms of a theoretical understanding of how the underlying physics shapes the geometry of the pattern manifold, altering the transport paths of patterns and the nature of pattern interpolation. We finally conclude by showing how optimal control can be utilized to generate complex patterns via an iterative control protocol over pattern forming pdes which can be casted as gradient flows. All together, our study shows how we can systematically build in physical priors into a generative framework for pattern control in non-equilibrium systems across multiple length and time scales.

Non-planar snake gaits: from Stigmatic-starts to Sidewinding

Of the vast variety of animal gaits, one of the most striking is the non-planar undulating motion of a sidewinder. But non-planar gaits are not limited to sidewinders. Here we report a new non-planar mode used as an escape strategy in juvenile anacondas (Eunectes notaeus). In the S-start, named for its eponymous shape, transient locomotion arises when the snake writhes and bends out of the plane while rolling forward about its midsection without slippage. To quantify our observations, we present a mathematical model for an active non-planar filament that interacts anisotropically with a frictional substrate and show that locomotion is due to a propagating localized pulse of a topological quantity, the link density. A two-dimensional phase space characterized by scaled body weight and muscular torque shows that relatively light juveniles are capable of S-starts but heavy adults are not, consistent with our experiments. Finally, we show that a periodic sequence of S-starts naturally leads to a sidewinding gait. All together, our characterization of a novel escape strategy in snakes highlights the role of topology in locomotion, provides a phase diagram for mode feasibility as a function of body size, and suggests a role for the S-start in the evolution of sidewinding.

Optimal shepherding and transport of a flock

We investigate how a shepherd should move in order to effectively herd and guide a flock of agents towards a target. Using a detailed agent-based model (ABM) for the members of the flock, we pose and solve an optimization problem for the shepherd that has to simultaneously work to keep the flock cohesive while coercing it towards a prescribed project. We find that three distinct strategies emerge as potential solutions as a function of just two parameters: the ratio of herd size to shepherd repulsion length and the ratio of herd speed to shepherd speed. We term these as: (i) mustering, in which the shepherd circles the herd to ensure compactness, (ii) droving, in which the shepherd chases the herd in a desired direction, and (iii) driving, a hitherto unreported strategy where the flock surrounds a shepherd that drives it from within. A minimal dynamical model for the size, shape and position of the herd captures the effective behavior of the ABM, and further allows us to characterize the different herding strategies in terms of the behavior of the shepherd that librates (mustering), oscillates (droving) or moves steadily (driving). All together, our study yields a simple and intuitive classification of herding strategies that ought to be of general interest in the context of controlling the collective behavior of active matter.

Modular representation and control of floppy networks

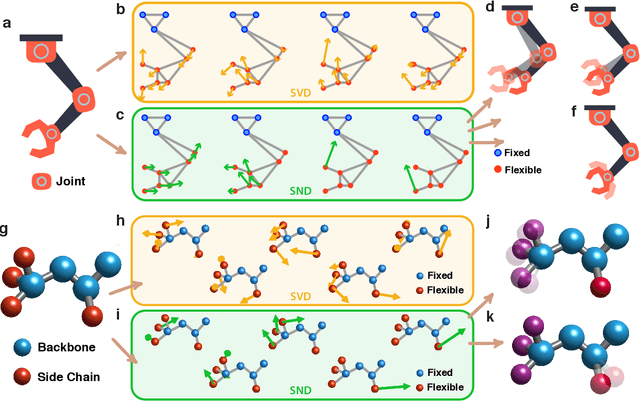
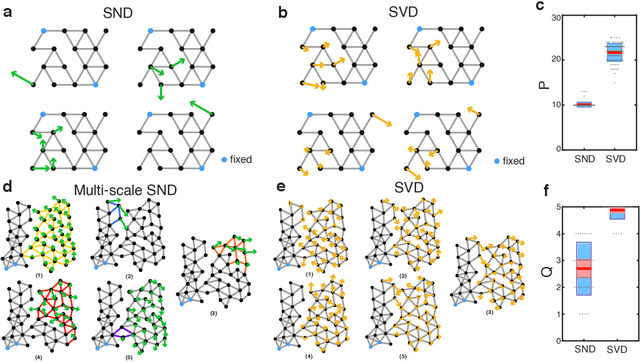
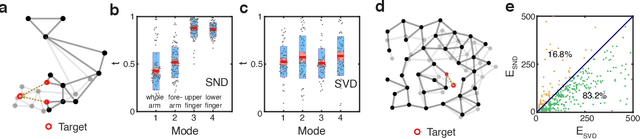
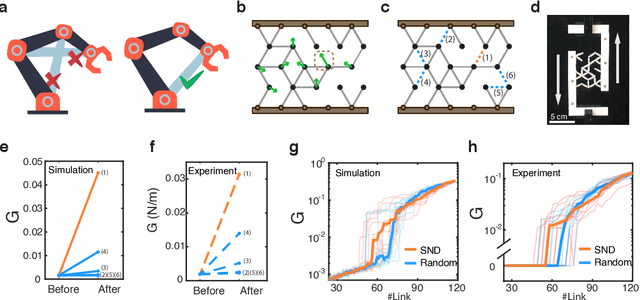
Geometric graph models of systems as diverse as proteins, robots, and mechanical structures from DNA assemblies to architected materials point towards a unified way to represent and control them in space and time. While much work has been done in the context of characterizing the behavior of these networks close to critical points associated with bond and rigidity percolation, isostaticity, etc., much less is known about floppy, under-constrained networks that are far more common in nature and technology. Here we combine geometric rigidity and algebraic sparsity to provide a framework for identifying the zero-energy floppy modes via a representation that illuminates the underlying hierarchy and modularity of the network, and thence the control of its nestedness and locality. Our framework allows us to demonstrate a range of applications of this approach that include robotic reaching tasks with motion primitives, and predicting the linear and nonlinear response of elastic networks based solely on infinitesimal rigidity and sparsity, which we test using physical experiments. Our approach is thus likely to be of use broadly in dissecting the geometrical properties of floppy networks using algebraic sparsity to optimize their function and performance.

Models of benthic bipedalism

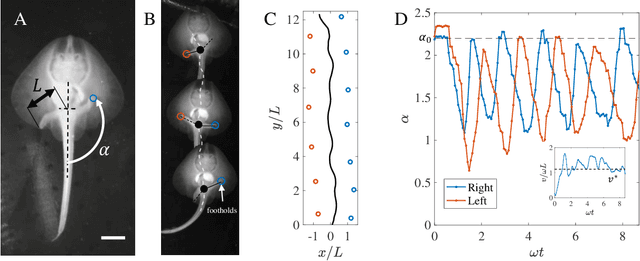
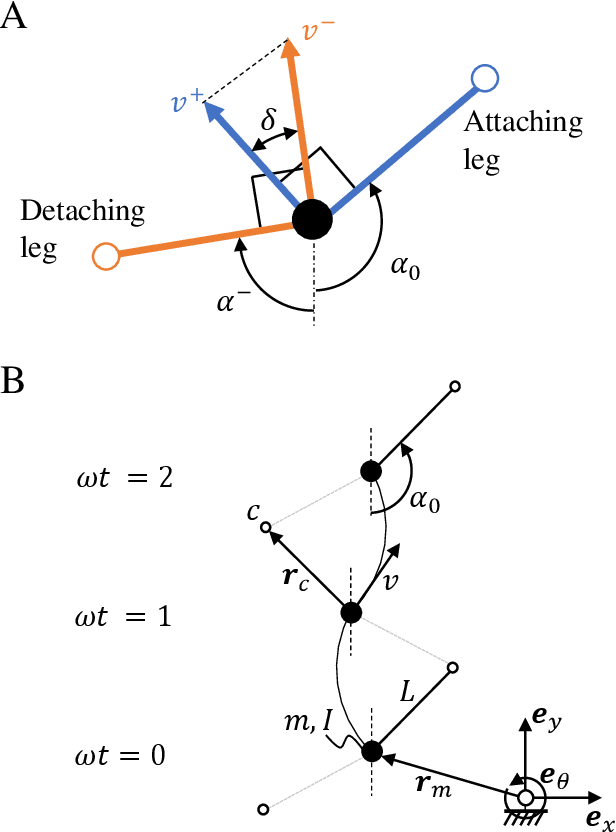
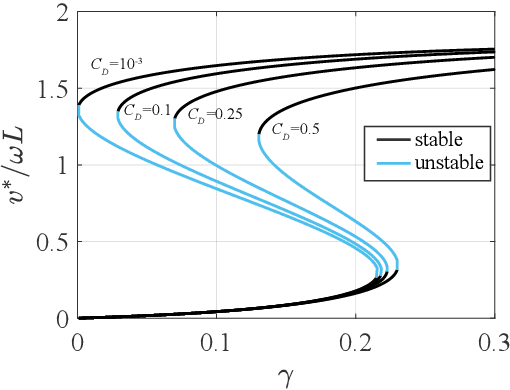
Walking is a common bipedal and quadrupedal gait and is often associated with terrestrial and aquatic organisms. Inspired by recent evidence of the neural underpinnings of primitive aquatic walking in the little skate Leucoraja erinacea, we introduce a theoretical model of aquatic walking that reveals robust and efficient gaits with modest requirements for body morphology and control. The model predicts undulatory behavior of the system body with a regular foot placement pattern which is also observed in the animal, and additionally predicts the existence of gait bistability between two states, one with a large energetic cost for locomotion and another associated with almost no energetic cost. We show that these can be discovered using a simple reinforcement learning scheme. To test these theoretical frameworks, we built a bipedal robot and show that its behaviors are similar to those of our minimal model: its gait is also periodic and exhibits bistability, with a low efficiency gait separated from a high efficiency gait by a "jump" transition. Overall, our study highlights the physical constraints on the evolution of walking and provides a guide for the design of efficient biomimetic robots.