Collective phototactic robotectonics

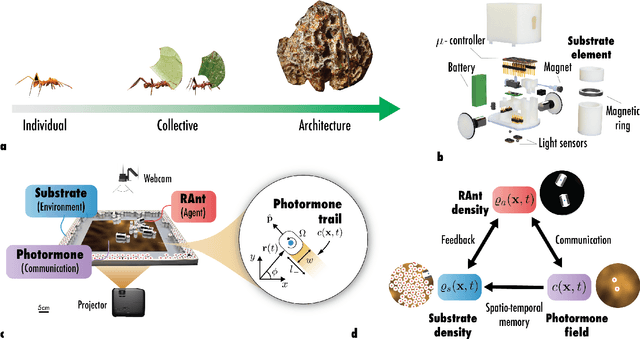
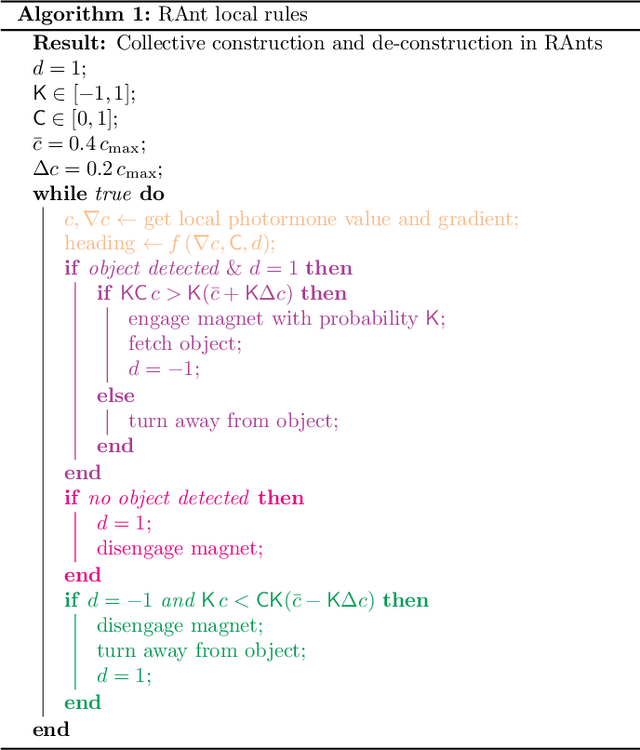
Cooperative task execution, a hallmark of eusociality, is enabled by local interactions between the agents and the environment through a dynamically evolving communication signal. Inspired by the collective behavior of social insects whose dynamics is modulated by interactions with the environment, we show that a robot collective can successfully nucleate a construction site via a trapping instability and cooperatively build organized structures. The same robot collective can also perform de-construction with a simple change in the behavioral parameter. These behaviors belong to a two-dimensional phase space of cooperative behaviors defined by agent-agent interaction (cooperation) along one axis and the agent-environment interaction (collection and deposition) on the other. Our behavior-based approach to robot design combined with a principled derivation of local rules enables the collective to solve tasks with robustness to a dynamically changing environment and a wealth of complex behaviors.

Modular representation and control of floppy networks

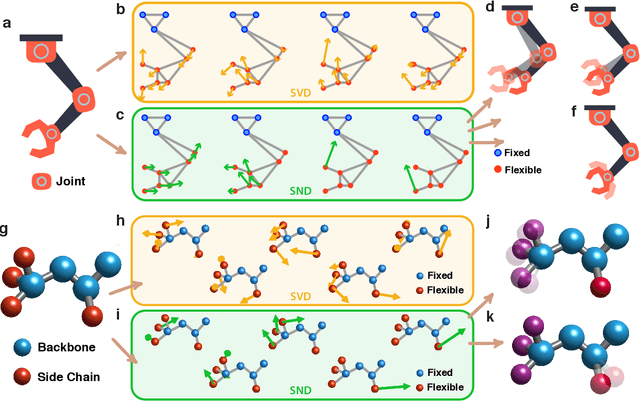
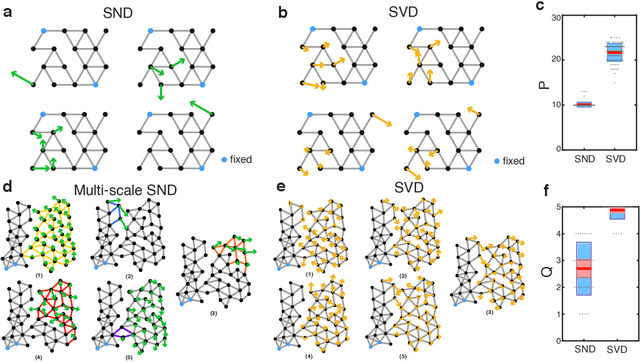
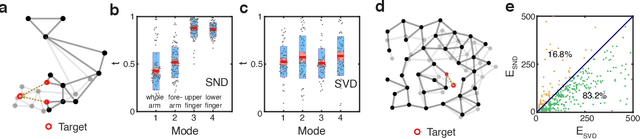
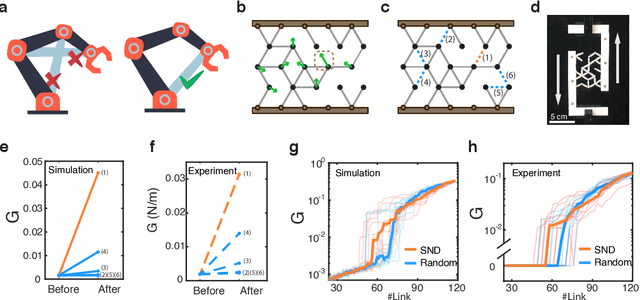
Geometric graph models of systems as diverse as proteins, robots, and mechanical structures from DNA assemblies to architected materials point towards a unified way to represent and control them in space and time. While much work has been done in the context of characterizing the behavior of these networks close to critical points associated with bond and rigidity percolation, isostaticity, etc., much less is known about floppy, under-constrained networks that are far more common in nature and technology. Here we combine geometric rigidity and algebraic sparsity to provide a framework for identifying the zero-energy floppy modes via a representation that illuminates the underlying hierarchy and modularity of the network, and thence the control of its nestedness and locality. Our framework allows us to demonstrate a range of applications of this approach that include robotic reaching tasks with motion primitives, and predicting the linear and nonlinear response of elastic networks based solely on infinitesimal rigidity and sparsity, which we test using physical experiments. Our approach is thus likely to be of use broadly in dissecting the geometrical properties of floppy networks using algebraic sparsity to optimize their function and performance.