Reactive Robot Navigation Using Quasi-conformal Mappings and Control Barrier Functions

This paper presents a robot control algorithm suitable for safe reactive navigation tasks in cluttered environments. The proposed approach consists of transforming the robot workspace into the \emph{ball world}, an artificial representation where all obstacle regions are closed balls. Starting from a polyhedral representation of obstacles in the environment, obtained using exteroceptive sensor readings, a computationally efficient mapping to ball-shaped obstacles is constructed using quasi-conformal mappings and M\"obius transformations. The geometry of the ball world is amenable to provably safe navigation tasks achieved via control barrier functions employed to ensure collision-free robot motions with guarantees both on safety and on the absence of deadlocks. The performance of the proposed navigation algorithm is showcased and analyzed via extensive simulations and experiments performed using different types of robotic systems, including manipulators and mobile robots.

Automatic Landmark Detection and Registration of Brain Cortical Surfaces via Quasi-Conformal Geometry and Convolutional Neural Networks

In medical imaging, surface registration is extensively used for performing systematic comparisons between anatomical structures, with a prime example being the highly convoluted brain cortical surfaces. To obtain a meaningful registration, a common approach is to identify prominent features on the surfaces and establish a low-distortion mapping between them with the feature correspondence encoded as landmark constraints. Prior registration works have primarily focused on using manually labeled landmarks and solving highly nonlinear optimization problems, which are time-consuming and hence hinder practical applications. In this work, we propose a novel framework for the automatic landmark detection and registration of brain cortical surfaces using quasi-conformal geometry and convolutional neural networks. We first develop a landmark detection network (LD-Net) that allows for the automatic extraction of landmark curves given two prescribed starting and ending points based on the surface geometry. We then utilize the detected landmarks and quasi-conformal theory for achieving the surface registration. Specifically, we develop a coefficient prediction network (CP-Net) for predicting the Beltrami coefficients associated with the desired landmark-based registration and a mapping network called the disk Beltrami solver network (DBS-Net) for generating quasi-conformal mappings from the predicted Beltrami coefficients, with the bijectivity guaranteed by quasi-conformal theory. Experimental results are presented to demonstrate the effectiveness of our proposed framework. Altogether, our work paves a new way for surface-based morphometry and medical shape analysis.

Modular representation and control of floppy networks

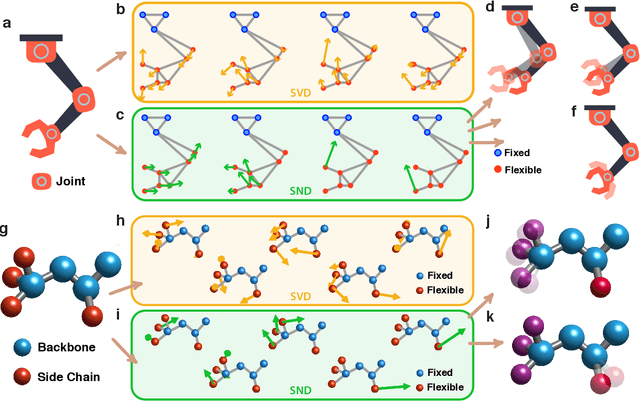
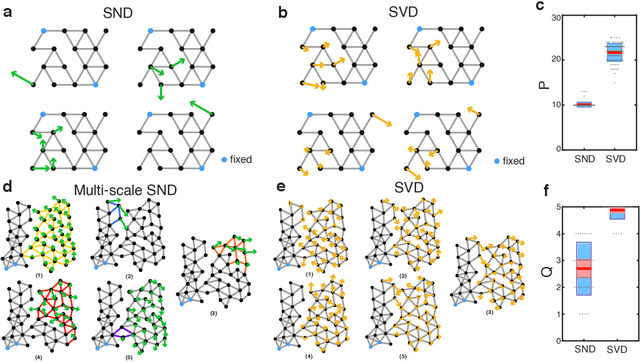
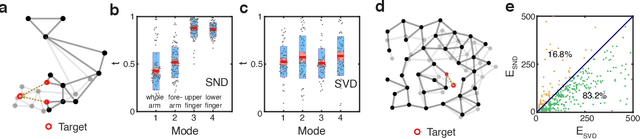
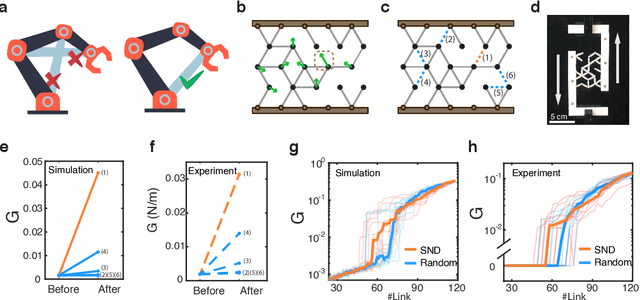
Geometric graph models of systems as diverse as proteins, robots, and mechanical structures from DNA assemblies to architected materials point towards a unified way to represent and control them in space and time. While much work has been done in the context of characterizing the behavior of these networks close to critical points associated with bond and rigidity percolation, isostaticity, etc., much less is known about floppy, under-constrained networks that are far more common in nature and technology. Here we combine geometric rigidity and algebraic sparsity to provide a framework for identifying the zero-energy floppy modes via a representation that illuminates the underlying hierarchy and modularity of the network, and thence the control of its nestedness and locality. Our framework allows us to demonstrate a range of applications of this approach that include robotic reaching tasks with motion primitives, and predicting the linear and nonlinear response of elastic networks based solely on infinitesimal rigidity and sparsity, which we test using physical experiments. Our approach is thus likely to be of use broadly in dissecting the geometrical properties of floppy networks using algebraic sparsity to optimize their function and performance.

Adaptive area-preserving parameterization of open and closed anatomical surfaces

The parameterization of open and closed anatomical surfaces is of fundamental importance in many biomedical applications. Spherical harmonics, a set of basis functions defined on the unit sphere, are widely used for anatomical shape description. However, establishing a one-to-one correspondence between the object surface and the entire unit sphere may induce a large geometric distortion in case the shape of the surface is too different from a perfect sphere. In this work, we propose adaptive area-preserving parameterization methods for simply-connected open and closed surfaces with the target of the parameterization being a spherical cap. Our methods optimize the shape of the parameter domain along with the mapping from the object surface to the parameter domain. The object surface will be globally mapped to an optimal spherical cap region of the unit sphere in an area-preserving manner while also exhibiting low conformal distortion. We further develop a set of spherical harmonics-like basis functions defined over the adaptive spherical cap domain, which we call the adaptive harmonics. Experimental results show that the proposed parameterization methods outperform the existing methods for both open and closed anatomical surfaces in terms of area and angle distortion. Surface description of the object surfaces can be effectively achieved using a novel combination of the adaptive parameterization and the adaptive harmonics. Our work provides a novel way of mapping anatomical surfaces with improved accuracy and greater flexibility. More broadly, the idea of using an adaptive parameter domain allows easy handling of a wide range of biomedical shapes.

A unifying framework for $n$-dimensional quasi-conformal mappings

With the advancement of computer technology, there is a surge of interest in effective mapping methods for objects in higher-dimensional spaces. To establish a one-to-one correspondence between objects, higher-dimensional quasi-conformal theory can be utilized for ensuring the bijectivity of the mappings. In addition, it is often desirable for the mappings to satisfy certain prescribed geometric constraints and possess low distortion in conformality or volume. In this work, we develop a unifying framework for computing $n$-dimensional quasi-conformal mappings. More specifically, we propose a variational model that integrates quasi-conformal distortion, volumetric distortion, landmark correspondence, intensity mismatch and volume prior information to handle a large variety of deformation problems. We further prove the existence of a minimizer for the proposed model and devise efficient numerical methods to solve the optimization problem. We demonstrate the effectiveness of the proposed framework using various experiments in two- and three-dimensions, with applications to medical image registration, adaptive remeshing and shape modeling.

Shape analysis via inconsistent surface registration

In this work, we develop a framework for shape analysis using inconsistent surface mapping. Traditional landmark-based geometric morphometrics methods suffer from the limited degrees of freedom, while most of the more advanced non-rigid surface mapping methods rely on a strong assumption of the global consistency of two surfaces. From a practical point of view, given two anatomical surfaces with prominent feature landmarks, it is more desirable to have a method that automatically detects the most relevant parts of the two surfaces and finds the optimal landmark-matching alignment between those parts, without assuming any global 1-1 correspondence between the two surfaces. Our method is capable of solving this problem using inconsistent surface registration based on quasi-conformal theory. It further enables us to quantify the dissimilarity of two shapes using quasi-conformal distortion and differences in mean and Gaussian curvatures, thereby providing a natural way for shape classification. Experiments on Platyrrhine molars demonstrate the effectiveness of our method and shed light on the interplay between function and shape in nature.

3DPeople: Modeling the Geometry of Dressed Humans

Recent advances in 3D human shape estimation build upon parametric representations that model very well the shape of the naked body, but are not appropriate to represent the clothing geometry. In this paper, we present an approach to model dressed humans and predict their geometry from single images. We contribute in three fundamental aspects of the problem, namely, a new dataset, a novel shape parameterization algorithm and an end-to-end deep generative network for predicting shape. First, we present 3DPeople, a large-scale synthetic dataset with 2.5 Million photo-realistic images of 80 subjects performing 70 activities and wearing diverse outfits. Besides providing textured 3D meshes for clothes and body, we annotate the dataset with segmentation masks, skeletons, depth, normal maps and optical flow. All this together makes 3DPeople suitable for a plethora of tasks. We then represent the 3D shapes using 2D geometry images. To build these images we propose a novel spherical area-preserving parameterization algorithm based on the optimal mass transportation method. We show this approach to improve existing spherical maps which tend to shrink the elongated parts of the full body models such as the arms and legs, making the geometry images incomplete. Finally, we design a multi-resolution deep generative network that, given an input image of a dressed human, predicts his/her geometry image (and thus the clothed body shape) in an end-to-end manner. We obtain very promising results in jointly capturing body pose and clothing shape, both for synthetic validation and on the wild images.

Tooth morphometry using quasi-conformal theory

Shape analysis is important in anthropology, bioarchaeology and forensic science for interpreting useful information from human remains. In particular, teeth are morphologically stable and hence well-suited for shape analysis. In this work, we propose a framework for tooth morphometry using quasi-conformal theory. Landmark-matching Teichm\"uller maps are used for establishing a 1-1 correspondence between tooth surfaces with prescribed anatomical landmarks. Then, a quasi-conformal statistical shape analysis model based on the Teichm\"uller mapping results is proposed for building a tooth classification scheme. We deploy our framework on a dataset of human premolars to analyze the tooth shape variation among genders and ancestries. Experimental results show that our method achieves much higher classification accuracy with respect to both gender and ancestry when compared to the existing methods. Furthermore, our model reveals the underlying tooth shape difference between different genders and ancestries in terms of the local geometric distortion and curvatures.

Area-preserving mapping of 3D ultrasound carotid artery images using density-equalizing reference map

Carotid atherosclerosis is a focal disease at the bifurcations of the carotid artery. To quantitatively monitor the local changes in the vessel-wall-plus-plaque thickness (VWT) and compare the VWT distributions for different patients or for the same patients at different ultrasound scanning sessions, a mapping technique is required to adjust for the geometric variability of different carotid artery models. In this work, we propose a novel method called density-equalizing reference map (DERM) for mapping 3D carotid surfaces to a standardized 2D carotid template, with an emphasis on preserving the local geometry of the carotid surface by minimizing the local area distortion. The initial map was generated by a previously described arc-length scaling (ALS) mapping method, which projects a 3D carotid surface onto a 2D non-convex L-shaped domain. A smooth and area-preserving flattened map was subsequently constructed by deforming the ALS map using the proposed algorithm that combines the density-equalizing map and the reference map techniques. This combination allows, for the first time, one-to-one mapping from a 3D surface to a standardized non-convex planar domain in an area-preserving manner. Evaluations using 20 carotid surface models show that the proposed method reduced the area distortion of the flattening maps by over 80% as compared to the ALS mapping method.