Revisiting the Misspecified Cramér-Rao Bound

Estimation under model misspecification arises in many signal processing problems, where the assumed observation model deviates from the true data-generating mechanism due to errors or simplifications. The misspecified Cramér-Rao bound (MCRB) is a widely recognized mean-squared-error (MSE) lower bound for this case, which has originally been used to describe the asymptotic behavior of the misspecified maximum likelihood (MML) estimator. Despite its widespread use, the MCRB lacks a rigorous characterization of the class of estimators for which it is valid. In this paper, we revisit the theory of parameter estimation under model misspecification and re-examine the foundations of the MCRB. We first demonstrate these limitations and examine a naive version of the MCRB, which relies only on local misspecified unbiasedness. We show that this bound is generally not tight and may be unattainable. To obtain a meaningful bound, we develop a new derivation based on the concept of pointwise equivalent models. By maximizing the naive bound for these models, we recover the classical MCRB, now supported by a constructive derivation, an explicit characterization of the associated estimator class, and an equality condition. This formulation establishes a formal link between local unbiasedness conditions and achievable bounds, offering new insights into the MCRB structure and its relevance to practical estimators. Finally, we define the notion of an efficient misspecified estimator and show that if it exists, it is achieved by the MML estimator.

Online Learning of Modular Bayesian Deep Receivers: Single-Step Adaptation with Streaming Data

Deep neural network (DNN)-based receivers offer a powerful alternative to classical model-based designs for wireless communication, especially in complex and nonlinear propagation environments. However, their adoption is challenged by the rapid variability of wireless channels, which makes pre-trained static DNN-based receivers ineffective, and by the latency and computational burden of online stochastic gradient descent (SGD)-based learning. In this work, we propose an online learning framework that enables rapid low-complexity adaptation of DNN-based receivers. Our approach is based on two main tenets. First, we cast online learning as Bayesian tracking in parameter space, enabling a single-step adaptation, which deviates from multi-epoch SGD . Second, we focus on modular DNN architectures that enable parallel, online, and localized variational Bayesian updates. Simulations with practical communication channels demonstrate that our proposed online learning framework can maintain a low error rate with markedly reduced update latency and increased robustness to channel dynamics as compared to traditional gradient descent based method.

Weighted Bayesian Cram$\acute{\text{e}}$r-Rao Bound for Mixed-Resolution Parameter Estimation

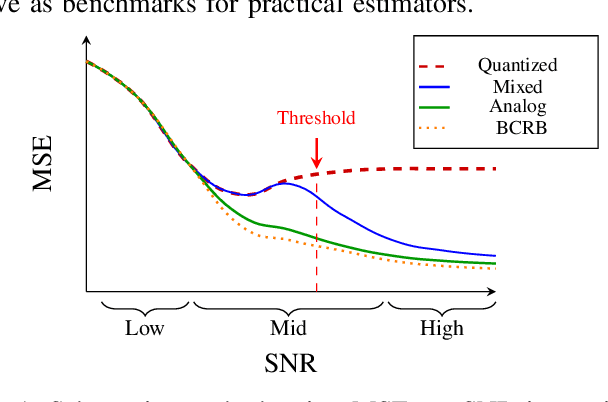
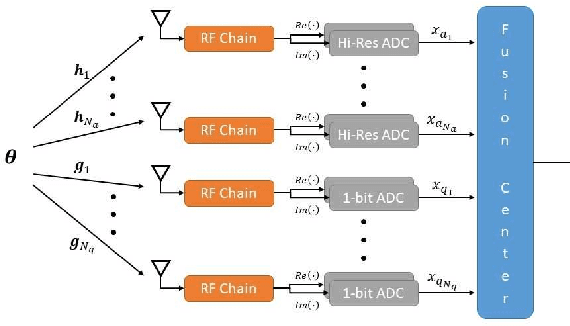
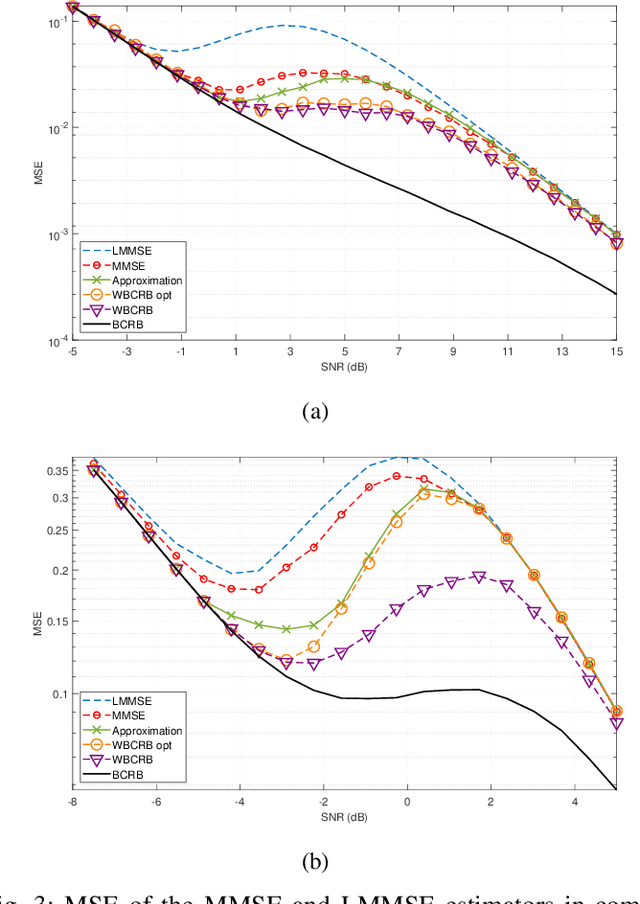
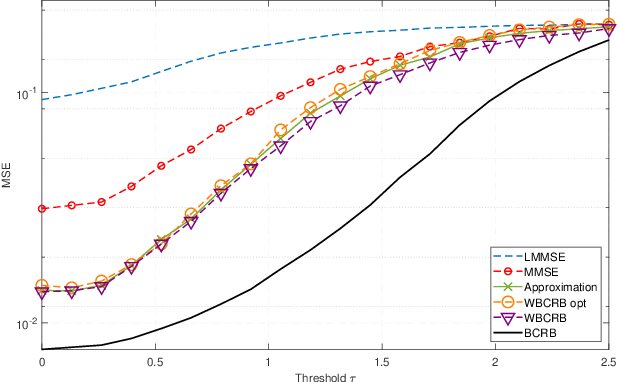
Mixed-resolution architectures, combining high-resolution (analog) data with coarsely quantized (e.g., 1-bit) data, are widely employed in emerging communication and radar systems to reduce hardware costs and power consumption. However, the use of coarsely quantized data introduces non-trivial tradeoffs in parameter estimation tasks. In this paper, we investigate the derivation of lower bounds for such systems. In particular, we develop the weighted Bayesian Cramer-Rao bound (WBCRB) for the mixed-resolution setting with a general weight function. We demonstrate the special cases of: (i) the classical BCRB; (ii) the WBCRB that is based on the Bayesian Fisher information matrix (BFIM)-Inverse weighting; and (iii) the Aharon-Tabrikian tightest WBCRB with an optimal weight function. Based on the developed WBCRB, we propose a new method to approximate the mean-squared-error (MSE) by partitioning the estimation problem into two regions: (a) where the 1-bit quantized data is informative; and (b) where it is saturated. We apply region-specific WBCRB approximations in these regions to achieve an accurate composite MSE estimate. We derive the bounds and MSE approximation for the linear Gaussian orthonormal (LGO) model, which is commonly used in practical signal processing applications. Our simulation results demonstrate the use of the proposed bounds and approximation method in the LGO model with a scalar unknown parameter. It is shown that the WBCRB outperforms the BCRB, where the BFIM-Inverse weighting version approaches the optimal WBCRB. Moreover, it is shown that the WBCRB-based MSE approximation is tighter and accurately predicts the non-monotonic behavior of the MSE in the presence of quantization errors.

Cramer-Rao Bounds for Laplacian Matrix Estimation

In this paper, we analyze the performance of the estimation of Laplacian matrices under general observation models. Laplacian matrix estimation involves structural constraints, including symmetry and null-space properties, along with matrix sparsity. By exploiting a linear reparametrization that enforces the structural constraints, we derive closed-form matrix expressions for the Cramer-Rao Bound (CRB) specifically tailored to Laplacian matrix estimation. We further extend the derivation to the sparsity-constrained case, introducing two oracle CRBs that incorporate prior information of the support set, i.e. the locations of the nonzero entries in the Laplacian matrix. We examine the properties and order relations between the bounds, and provide the associated Slepian-Bangs formula for the Gaussian case. We demonstrate the use of the new CRBs in three representative applications: (i) topology identification in power systems, (ii) graph filter identification in diffused models, and (iii) precision matrix estimation in Gaussian Markov random fields under Laplacian constraints. The CRBs are evaluated and compared with the mean-squared-errors (MSEs) of the constrained maximum likelihood estimator (CMLE), which integrates both equality and inequality constraints along with sparsity constraints, and of the oracle CMLE, which knows the locations of the nonzero entries of the Laplacian matrix. We perform this analysis for the applications of power system topology identification and graphical LASSO, and demonstrate that the MSEs of the estimators converge to the CRB and oracle CRB, given a sufficient number of measurements.

Efficient Sampling Allocation Strategies for General Graph-Filter-Based Signal Recovery

Sensor placement plays a crucial role in graph signal recovery in underdetermined systems. In this paper, we present the graph-filtered regularized maximum likelihood (GFR-ML) estimator of graph signals, which integrates general graph filtering with regularization to enhance signal recovery performance under a limited number of sensors. Then, we investigate task-based sampling allocation aimed at minimizing the mean squared error (MSE) of the GFR-ML estimator by wisely choosing sensor placement. Since this MSE depends on the unknown graph signals to be estimated, we propose four cost functions for the optimization of the sampling allocation: the biased Cram$\acute{\text{e}}$r-Rao bound (bCRB), the worst-case MSE (WC-MSE), the Bayesian MSE (BMSE), and the worst-case BMSE (WC-BMSE), where the last two assume a Gaussian prior. We investigate the properties of these cost functions and develop two algorithms for their practical implementation: 1) the straightforward greedy algorithm; and 2) the alternating projection gradient descent (PGD) algorithm that reduces the computational complexity. Simulation results on synthetic and real-world datasets of the IEEE 118-bus power system and the Minnesota road network demonstrate that the proposed sampling allocation methods reduce the MSE by up to $50\%$ compared to the common sampling methods A-design, E-design, and LR-design in the tested scenarios. Thus, the proposed methods improve the estimation performance and reduce the required number of measurements in graph signal processing (GSP)-based signal recovery in the case of underdetermined systems.

Recovery of Sparse Graph Signals

This paper investigates the recovery of a node-domain sparse graph signal from the output of a graph filter. This problem, often referred to as the identification of the source of a diffused sparse graph signal, is seminal in the field of graph signal processing (GSP). Sparse graph signals can be used in the modeling of a variety of real-world applications in networks, such as social, biological, and power systems, and enable various GSP tasks, such as graph signal reconstruction, blind deconvolution, and sampling. In this paper, we assume double sparsity of both the graph signal and the graph topology, as well as a low-order graph filter. We propose three algorithms to reconstruct the support set of the input sparse graph signal from the graph filter output samples, leveraging these assumptions and the generalized information criterion (GIC). First, we describe the graph multiple GIC (GM-GIC) method, which is based on partitioning the dictionary elements (graph filter matrix columns) that capture information on the signal into smaller subsets. Then, the local GICs are computed for each subset and aggregated to make a global decision. Second, inspired by the well-known branch and bound (BNB) approach, we develop the graph-based branch and bound GIC (graph-BNB-GIC), and incorporate a new tractable heuristic bound tailored to the graph and graph filter characteristics. Finally, we propose the graph-based first order correction (GFOC) method, which improves existing sparse recovery methods by iteratively examining potential improvements to the GIC cost function through replacing elements from the estimated support set with elements from their one-hop neighborhood. We conduct simulations that demonstrate that the proposed sparse recovery methods outperform existing methods in terms of support set recovery accuracy, and without a significant computational overhead.

Leaky Waveguide Antennas for Downlink Wideband THz Communications

THz communications are expected to play a profound role in future wireless systems. The current trend of the extremely massive multiple-input multiple-output (MIMO) antenna architectures tends to be costly and power inefficient when implementing wideband THz communications. An emerging THz antenna technology is leaky wave antenna (LWA), which can realize frequency selective beamforming with a single radiating element. In this work, we explore the usage of LWAs technology for wideband multi-user THz communications. We propose a model for the LWA signal processing that is physically compliant facilitating studying LWA-aided communication systems. Focusing on downlink systems, we propose an alternating optimization algorithm for jointly optimizing the LWA configuration along with the signal spectral power allocation to maximize the sum-rate performance. Our numerical results show that a single LWA can generate diverse beampatterns at THz, exhibiting performance comparable to costly fully digital MIMO arrays.

GSP-KalmanNet: Tracking Graph Signals via Neural-Aided Kalman Filtering

Dynamic systems of graph signals are encountered in various applications, including social networks, power grids, and transportation. While such systems can often be described as state space (SS) models, tracking graph signals via conventional tools based on the Kalman filter (KF) and its variants is typically challenging. This is due to the nonlinearity, high dimensionality, irregularity of the domain, and complex modeling associated with real-world dynamic systems of graph signals. In this work, we study the tracking of graph signals using a hybrid model-based/data-driven approach. We develop the GSP-KalmanNet, which tracks the hidden graphical states from the graphical measurements by jointly leveraging graph signal processing (GSP) tools and deep learning (DL) techniques. The derivations of the GSP-KalmanNet are based on extending the KF to exploit the inherent graph structure via graph frequency domain filtering, which considerably simplifies the computational complexity entailed in processing high-dimensional signals and increases the robustness to small topology changes. Then, we use data to learn the Kalman gain following the recently proposed KalmanNet framework, which copes with partial and approximated modeling, without forcing a specific model over the noise statistics. Our empirical results demonstrate that the proposed GSP-KalmanNet achieves enhanced accuracy and run time performance as well as improved robustness to model misspecifications compared with both model-based and data-driven benchmarks.

NUV-DoA: NUV Prior-based Bayesian Sparse Reconstruction with Spatial Filtering for Super-Resolution DoA Estimation

Achieving high-resolution Direction of Arrival (DoA) recovery typically requires high Signal to Noise Ratio (SNR) and a sufficiently large number of snapshots. This paper presents NUV-DoA algorithm, that augments Bayesian sparse reconstruction with spatial filtering for super-resolution DoA estimation. By modeling each direction on the azimuth's grid with the sparsity-promoting normal with unknown variance (NUV) prior, the non-convex optimization problem is reduced to iteratively reweighted least-squares under Gaussian distribution, where the mean of the snapshots is a sufficient statistic. This approach not only simplifies our solution but also accurately detects the DoAs. We utilize a hierarchical approach for interference cancellation in multi-source scenarios. Empirical evaluations show the superiority of NUV-DoA, especially in low SNRs, compared to alternative DoA estimators.

Non-Bayesian Post-Model-Selection Estimation as Estimation Under Model Misspecification

In many parameter estimation problems, the exact model is unknown and is assumed to belong to a set of candidate models. In such cases, a predetermined data-based selection rule selects a parametric model from a set of candidates before the parameter estimation. The existing framework for estimation under model misspecification does not account for the selection process that led to the misspecified model. Moreover, in post-model-selection estimation, there are multiple candidate models chosen based on the observations, making the interpretation of the assumed model in the misspecified setting non-trivial. In this work, we present three interpretations to address the problem of non-Bayesian post-model-selection estimation as an estimation under model misspecification problem: the naive interpretation, the normalized interpretation, and the selective inference interpretation, and discuss their properties. For each of these interpretations, we developed the corresponding misspecified maximum likelihood estimator and the misspecified Cram$\acute{\text{e}}$r-Rao-type lower bound. The relations between the estimators and the performance bounds, as well as their properties, are discussed. Finally, we demonstrate the performance of the proposed estimators and bounds via simulations of estimation after channel selection. We show that the proposed performance bounds are more informative than the oracle Cram$\acute{\text{e}}$r-Rao Bound (CRB), where the third interpretation (selective inference) results in the lowest mean-squared-error (MSE) among the estimators.