Efficient Sampling Allocation Strategies for General Graph-Filter-Based Signal Recovery

Sensor placement plays a crucial role in graph signal recovery in underdetermined systems. In this paper, we present the graph-filtered regularized maximum likelihood (GFR-ML) estimator of graph signals, which integrates general graph filtering with regularization to enhance signal recovery performance under a limited number of sensors. Then, we investigate task-based sampling allocation aimed at minimizing the mean squared error (MSE) of the GFR-ML estimator by wisely choosing sensor placement. Since this MSE depends on the unknown graph signals to be estimated, we propose four cost functions for the optimization of the sampling allocation: the biased Cram$\acute{\text{e}}$r-Rao bound (bCRB), the worst-case MSE (WC-MSE), the Bayesian MSE (BMSE), and the worst-case BMSE (WC-BMSE), where the last two assume a Gaussian prior. We investigate the properties of these cost functions and develop two algorithms for their practical implementation: 1) the straightforward greedy algorithm; and 2) the alternating projection gradient descent (PGD) algorithm that reduces the computational complexity. Simulation results on synthetic and real-world datasets of the IEEE 118-bus power system and the Minnesota road network demonstrate that the proposed sampling allocation methods reduce the MSE by up to $50\%$ compared to the common sampling methods A-design, E-design, and LR-design in the tested scenarios. Thus, the proposed methods improve the estimation performance and reduce the required number of measurements in graph signal processing (GSP)-based signal recovery in the case of underdetermined systems.

Verifying the Smoothness of Graph Signals: A Graph Signal Processing Approach

Graph signal processing (GSP) deals with the representation, analysis, and processing of structured data, i.e. graph signals that are defined on the vertex set of a generic graph. A crucial prerequisite for applying various GSP and graph neural network (GNN) approaches is that the examined signals are smooth graph signals with respect to the underlying graph, or, equivalently, have low graph total variation (TV). In this paper, we develop GSP-based approaches to verify the validity of the smoothness assumption of given signals (data) and an associated graph. The proposed approaches are based on the representation of network data as the output of a graph filter with a given graph topology. In particular, we develop two smoothness detectors for the graph-filter-output model: 1) the likelihood ratio test (LRT) for known model parameters; and 2) a semi-parametric detector that estimates the graph filter and then validates its smoothness. The properties of the proposed GSP-based detectors are investigated, and some special cases are discussed. The performance of the GSP-based detectors is evaluated on synthetic data and on IEEE $14$-bus power system data, under different setups. The results demonstrate the effectiveness of the proposed approach and its robustness to different generating models, noise levels, and number of samples.

State Estimation in Unobservable Power Systems via Graph Signal Processing Tools

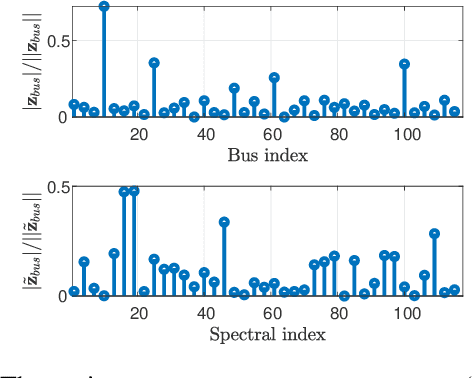
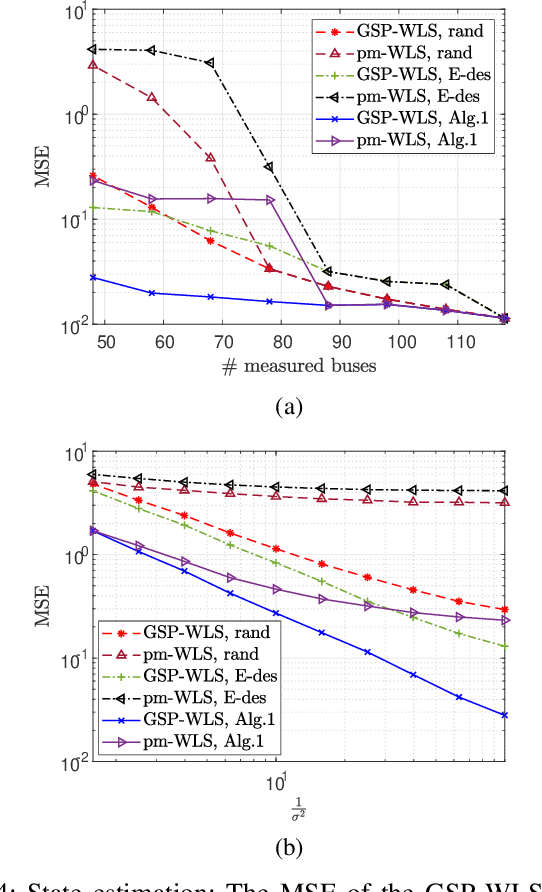
We consider the problem of estimating the states and detecting bad data in an unobservable power system. To this end, we propose novel graph signal processing (GSP) methods. The main assumption behind the proposed GSP approach is that the grid state vector, which includes the phases of the voltages in the system, is a smooth graph signal with respect to the system admittance matrix that represents the underlying graph. Thus, the first step in this paper is to validate the graph-smoothness assumption of the states, both empirically and theoretically. Then, we develop the regularized weighted least squares (WLS) state estimator, which does not require observability of the network. We propose a sensor (meter) placement strategy that aims to optimize the estimation performance of the proposed GSP-WLS estimator. In addition, we develop a joint bad-data and false data injected (FDI) attacks detector that integrates the GSP-WLS state estimator into the conventional J(theta)-test with an additional smoothness regularization. Numerical results on the IEEE 118-bus test-case system demonstrate that the new GSP methods outperform commonly-used estimation and detection approaches in electric networks and are robust to missing data.