State Estimation in Unobservable Power Systems via Graph Signal Processing Tools

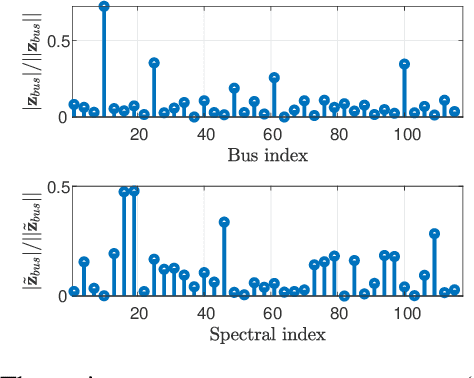
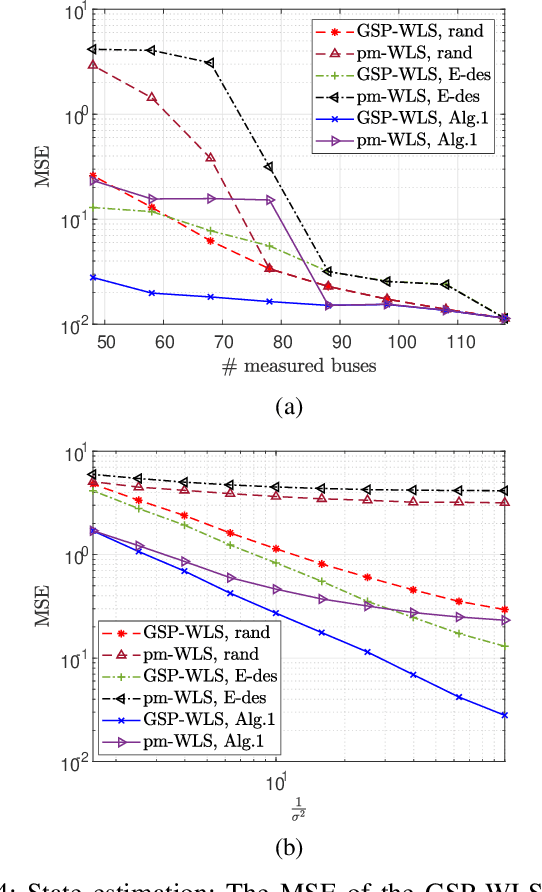
We consider the problem of estimating the states and detecting bad data in an unobservable power system. To this end, we propose novel graph signal processing (GSP) methods. The main assumption behind the proposed GSP approach is that the grid state vector, which includes the phases of the voltages in the system, is a smooth graph signal with respect to the system admittance matrix that represents the underlying graph. Thus, the first step in this paper is to validate the graph-smoothness assumption of the states, both empirically and theoretically. Then, we develop the regularized weighted least squares (WLS) state estimator, which does not require observability of the network. We propose a sensor (meter) placement strategy that aims to optimize the estimation performance of the proposed GSP-WLS estimator. In addition, we develop a joint bad-data and false data injected (FDI) attacks detector that integrates the GSP-WLS state estimator into the conventional J(theta)-test with an additional smoothness regularization. Numerical results on the IEEE 118-bus test-case system demonstrate that the new GSP methods outperform commonly-used estimation and detection approaches in electric networks and are robust to missing data.

Bayesian Estimation of Graph Signals

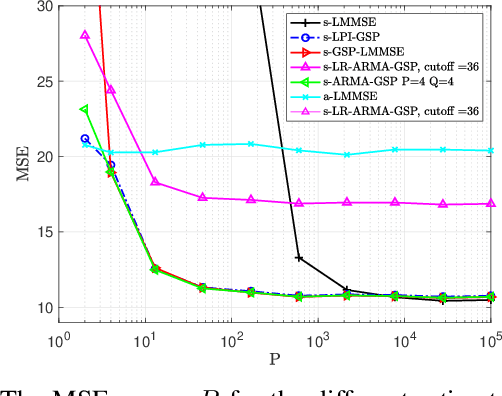
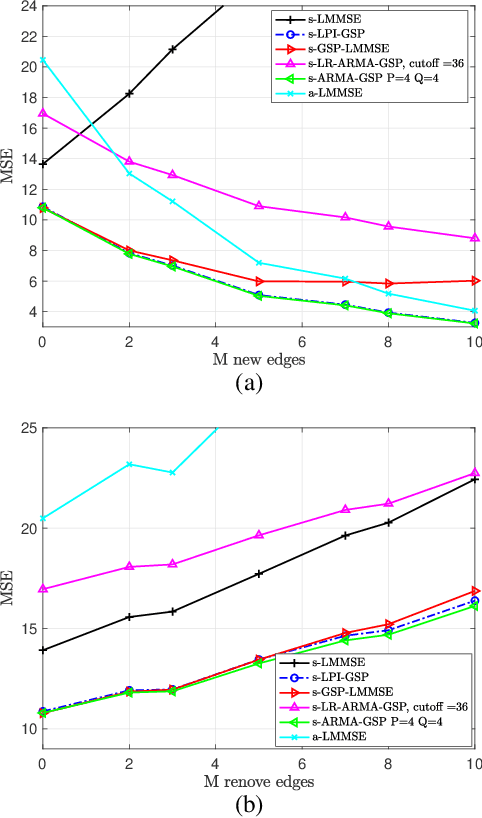
We consider the problem of recovering random graph signals from nonlinear measurements. For this case, closed-form Bayesian estimators are usually intractable and even numerical evaluation of these estimators may be hard to compute for large networks. In this paper, we propose a graph signal processing (GSP) framework for random graph signal recovery that utilizes the information of the structure behind the data. First, we develop the GSP-linear minimum mean-squared-error (GSP-LMMSE) estimator, which minimizes the mean-squared error (MSE) among estimators that are represented as an output of a graph filter. The GSP-LMMSE estimator is based on diagonal covariance matrices in the graph frequency domain, and thus, has reduced complexity compared with the LMMSE estimator. This property is especially important when using the sample-mean versions of these estimators that are based on a training dataset. We then state conditions under which the low-complexity GSP-LMMSE estimator coincides with the optimal LMMSE estimator. Next, we develop the approximated parametrization of the GSP-LMMSE estimator by shift-invariant graph filters by solving a weighted least squared (WLS) problem. We present three implementations of the parametric GSP-LMMSE estimator for typical graph filters. Parametric graph filters are more robust to outliers and to network topology changes. In our simulations, we evaluate the performance of the proposed GSP-LMMSE estimators for the problem of state estimation in power systems, which can be interpreted as a graph signal recovery task. We show that the proposed sample-GSP estimators outperform the sample-LMMSE estimator for a limited training dataset and that the parametric GSP-LMMSE estimators are more robust to topology changes in the form of adding/removing vertices/edges.